Название: Сегнетоэлектрики

Вид работы: статья

Рубрика: Математика

Размер файла: 50.09 Kb

Скачать файл: referat.me-218819.docx

Краткое описание работы: Сегнетоэлектрики представляют собой специфический класс сред, характеризующийся высоким значением диэлектрической проницаемости (на основной кривой поляризации).

Сегнетоэлектрики

М.И. Векслер, Г.Г. Зегря

Сегнетоэлектрики представляют собой специфический класс сред, характеризующийся высоким значением диэлектрической проницаемости (на основной кривой поляризации), нелинейностью зависимости , гистерезисом зависимостей D(E) и P(E), а также сохранением поляризованности после отключения внешнего поля. Именно последнее свойство наиболее важно, и во многих случаях под словом "сегнетоэлектрик" подразумевается "область спонтанной поляризованности ", слабо чувствительная к дополнительному наложению электрического поля.

Расчет поля сегнетоэлектриков производится следующим образом. По формулам

(50)

находится связанный заряд, а затем находится создаваемое им поле с помощью закона Кулона, как если бы этот заряд был свободным:

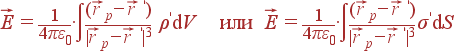(51)

Если есть выраженная симметрия, то возможно и применение теоремы Гаусса в виде . Мотивацией такого метода является уравнение Максвелла .

При наличии, помимо сегнетоэлектриков, еще и сторонних зарядов поле последних суммируется с полем сегнетоэлектриков.

Для нахождения смещения привлекается соотношение

(52)

При этом никаких ε для сегнетоэлектрика вводиться не должно.

Задача. Имеется бесконечная пластина из однородного сегнетоэлектрика с поляризованностью . Найти векторы и внутри и вне пластины, если вектор направлен a) перпендикулярно, b) параллельно поверхности пластины.

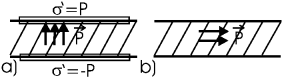Решение Разберемся прежде всего в том, какова будет в обоих случаях, то есть какие связанные заряды присутствуют. Для этого надо проверить, как изменяется в направлении самого себя. В случае б) , в том числе и на границах; на них , конечно, изменяется, но не в направлении . А вот в случае а) имеет место скачок от (до) нуля на границах как раз в направлении . Соответственно, поверхностная плотность заряда равна:

σ'(a) = ± P

причем знак плюс берется для той поверхности, в сторону которой "смотрит" вектор , по определению σ'. Как уже говорилось,

σ'(b) = 0

Следовательно, в случае а) мы имеем ситуацию, аналогичную конденсатору и получаем

в то время как

Заметим, что в случае а) ошибкой было бы записать D = σ'; теорема Гаусса применяется к вектору .

Соответственно, по формуле имеем:

	=
	=

Задача. Пластина из сегнетоэлектрика с поляризованностью P, перпендикулярной поверхностям, помещена в конденсатор, обкладки которого замкнуты друг на друга. Пластина занимает η-ю часть зазора и параллельна обкладкам конденсатора. Найти E и D в пластине и в остающемся незаполненным зазоре.

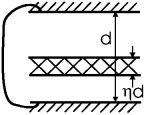Решение Если Eplate и Eair обозначают электрическое поле, соответственно, в пластине и в воздушном зазоре, то, ввиду замкнутости обкладок конденсатора друг на друга,

η Eplate +(1–η) Eair = 0

Величина D в зазоре и в пластине одна и та же, так как любой другой вариант противоречил бы условиям для нормальной компоненты D на границе пластина-воздух.

Dplate = ε0Eplate+P = Dair = ε0Eair

Из последней цепочки равенств имеем

Eair = Eplate+ε0–1P

Используя это, получаем

η Eplate +(1–η)(Eplate+ ε0–1P) = 0

откуда

Eplate = –(1–η)ε0–1P, Eair = ηε0–1P

Смещение всюду одно и то же и равно Dplate = Dair = η P.

Задача. Тонкий диск радиуса R из сегнетоэлектрического материала поляризован однородно и так, что вектор лежит в плоскости диска. Найти и в центре диска, считая, что толщина диска h намного меньше, чем R.

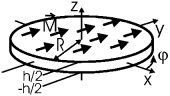Решение Введем систему координат так, чтобы плоскость xy была плоскостью диска, а . Найдем связанные заряды. всюду равна нулю, за исключением обода диска (на круглых поверхностях диска тоже , так как там не меняется в направлении ). Поверхностный заряд составит

σ' = –Pr|R+0+Pr|R–0 = Psinφ

где φ угол в полярной системе координат, отсчитываемый от оси x, как обычно. Зная σ', можно найти поле по закону Кулона ():

	=
=
=

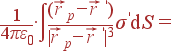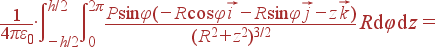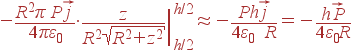При получении последнего равенства использовано условие R>> h. Обратим внимание на то, что при R→∞ .

Смещение найдется просто как

Список литературы

1. И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448 с.; или 2-е изд., М.: Наука, 1988. - 416 с.

2. В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М. Бредова), 2-е изд., М.: Наука, 1970. - 503 с.

3. Л.Д. Ландау, Е.М. Лифшиц, Теоретическая физика. т.8 Электродинамика сплошных сред, 2-е изд., М.: Наука, 1992. - 661 с.