Referat.me / Математика / Конус, и все что с ним связано

Название: Конус, и все что с ним связано

Вид работы: реферат

Размер файла: 56.4 Kb

Скачать файл: referat.me-218947.docx

Краткое описание работы: КОНУС 1. Понятие конуса: тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Коническая поверхность называется боковой поверхностью конуса, а круг – основанием конуса

Конус, и все что с ним связано

КОНУС

1. Понятие конуса: тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Коническая поверхность называется боковой поверхностью конуса, а круг – основанием конуса

2. Получение конуса: конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.

С2

С1

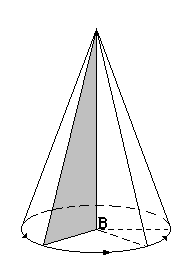
3. Сечение конуса: если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым.

Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О₁ , расположенной на оси конуса.

4. Площадь поверхности конуса: разверткой боковой поверхности конуса является круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора – длине окружности основания конуса. За площадь боковой поверхности конуса принимается площадь ее развертки.

А₁

где α – градусная мера дуги АВА₁

откуда

Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания.

5. Усеченный конус, его получение и площадь:

образующая

конуса

Основания

поверхность

боковая

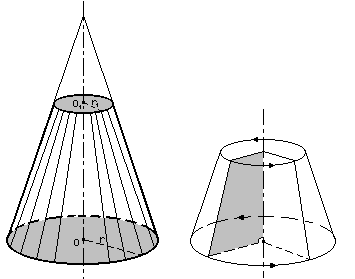
Усеченный конус может быть получен вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.

Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.

Похожие работы

Геометрические свойства регулярного круглого конуса в пространстве
Приведены явные формулы для вычисления множеств положительных и отрицательных частей произвольного элемента в пространстве , упорядоченном круглым регулярным конусом.
Конус, площадь его поверхности и объем
Систематизация и углубление знаний по теме “Конус”. Повысить интерес к геометрии, решая нестандартные задачи и отвечая на занимательные вопросы. Создание положительной внутренней мотивации обучения учащихся.
Цилиндр и конус
Определения и свойства цилиндра и конуса.
Формирование понятия цилиндра
I этап: Введение понятия цилиндр. Математическое видение цилиндра. Цель этапа Формирование пространственного представления и логического мышления учащихся при изучении и формировании математического видения цилиндра его характерных элементов и изображений.
Построение линии пересечения 2-х конусов и цилиндра
Министерство общего и профессионального образования РФ Брянский Государственный Технический Университет кафедра «Высшая математика» Расчетно-графическая работа №1
Все о Конусе
Муниципальное обще образовательное учреждение Средняя общеобразовательная школа №54 с углубленным изучение предметов социально-гуманитарного цикла центрального района города Новосибирска
Билеты по геометрии (11 класс)
Билет № 3 Взаимное расположение прямой и плоскости в пространстве Объем призмы. Три случая расположения прямой и плоскости. 1.Плоскость и прямая имеют одну оющую точку
Неединственность преобразований Лоренца.
Основа физики – геометрия. Она определяет способы задания координат. Преобразования их единственны и это преобразования Лоренца внутри изотропного конуса. На поверхности изотропного конуса эти преобразования не обладают единственностью. Расстояние света.
Задачи на наибольшее и наименьшее значения функций
Задачи на наибольшее и наименьшее значения функции Требуется изготовить коническую воронку с образующей l=10см. Каков должен быть радиус основания воронки, чтобы ее объем был наибольшим?
Тела вращения
Цилиндр. Конус. Шар. Пирамида. Правильная пирамида. Многогранники. Призма.