Название: по Физике 2
Вид работы: контрольная работа
Рубрика: Физика
Размер файла: 369.59 Kb
Скачать файл: referat.me-341656.docx
Краткое описание работы: Заказ №132919 Контрольная работа №1 №106 Дано: Найти: Решение В данном случае движение пули можно рассматривать как движение тела, брошенного горизонтально. Согласно основным уравнениям кинематики координаты пули будут изменяться со временем:
по Физике 2
Заказ №132919
Контрольная работа №1
№106
Дано:
![]()
Найти: ![]()
Решение
В данном случае движение пули можно рассматривать как движение тела, брошенного горизонтально. Согласно основным уравнениям кинематики координаты пули будут изменяться со временем:
![]() (1),
(1),
![]() (2).
(2).
Так как ![]() ,
, ![]() ,
, ![]() (вдоль оси х
пуля двигается равномерно
(вдоль оси х
пуля двигается равномерно ![]() ), то равенство (1) перепишем в виде:
), то равенство (1) перепишем в виде:
![]() (3).
(3).
Так как ![]() ,
, ![]() ,
, ![]() ( ось у
направляем вниз), то равенство (2) перепишем в виде:
( ось у
направляем вниз), то равенство (2) перепишем в виде:
![]() (4).
(4).
Учитывая, что в данном случае ![]() , то равенства (3) и (4) примут вид
, то равенства (3) и (4) примут вид
![]()
![]()
Тогда
![]()
и, соответственно,
![]()
Откуда находим
![]()
Подставив числовые значения, получаем
![]()
Ответ:
![]()
№116
Дано:
![]()
Найти: ![]()
Решение
Полное ускорение определяется как
![]()
где ![]() - нормальная составляющая ускорения,
- нормальная составляющая ускорения, ![]() - тангенциальная составляющая ускорения. Поскольку
- тангенциальная составляющая ускорения. Поскольку
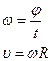
то
![]()
Тогда
![]()
Следовательно
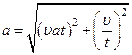
Подставив числовые значения, находим
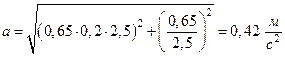
Ответ:
![]()
№126
Дано:
![]()
Найти: ![]()
Решение
Согласно второму закону Ньютона в данном случае справедливо
![]()
откуда можем найти угловую скорость
![]()
Так как по определению,
![]()
то
![]()
Откуда находим
![]()
Подставив числовые значения, получаем
![]()
Ответ:
![]()
№136
Дано:
а) т 1 =8 кг; υ1 =0; т 2 =2 кг; υ2 =5 м/с; б) т 1 =2 кг; υ1 =0; т 2 =8 кг; υ2 =5 м/с
Найти: и
а
; и
b
; ![]()
Решение.
Согласно закону сохранения импульса, учитывая неупругий удар, имеем
![]() (1)
(1)
Проецируем равенство (1) на координатную ось х (рис.1) и учитывая значения скоростей, получаем:
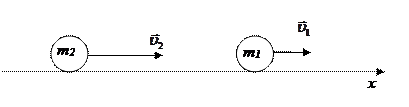
![]()
откуда
![]() .
.
Подставив значения из условия задачи для каждого случая, находим:
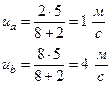
Работа деформации может быть определена как изменение кинетической энергии системы, т.е.
![]()
Тогда для каждого случая имеем
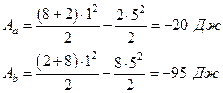
Знак «-» указывает на уменьшение кинетической энергии из-за затраты на деформацию.
Доля кинетической энергии, расходуемая на деформацию равна
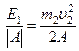
Для каждого случая имеем
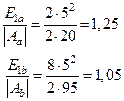
Ответ:
![]()
№146
Решение
Согласно закону динамики вращательного движения имеем:
![]()
где ![]() .Тогда
.Тогда
![]()
А) Цилиндр сплошной. Для него
![]()
Следовательно,
![]()
откуда
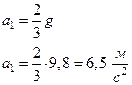
Б) Цилиндр тонкостенный. Для него
![]()
Следовательно,
![]()
откуда
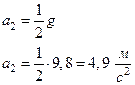
Ответ:
![]() ;
; ![]()
№156
Дано:
h =1 м
Найти: ![]()
Решение.
В начальный момент времени шар обладает только потенциальной энергией (т.к. ![]() )
)
![]()
В конце скатывания, так как скольжение отсутствует, согласно закону сохранения энергии вся потенциальная энергия превращается в кинетическую энергию поступательного и вращательного движения, т.е.
![]()
Так как по определению ![]() , то
, то
![]()
Таким образом, имеем
![]()
откуда
![]()
Подставив числовые значения, находим
![]()
Ответ:
![]()
№166
Дано:
![]()
Найти: ![]()
Решение
Период колебаний физического маятника определяется как
![]()
где ![]() - момент инерции маятника
- момент инерции маятника
Тогда
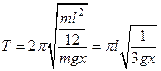
Понятно, что период колебаний маятника будет наименьшим при условии, что ![]()
Ответ:
![]()
№176
Дано:
![]()
Найти: ![]()
Решение
Уравнение волны
![]()
где ![]() - частота,
- частота, ![]() - скорость распространения волны. Тогда
- скорость распространения волны. Тогда
![]()
Подставив известные величины, получаем
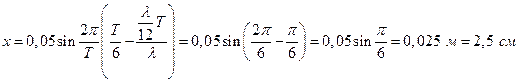
Ответ:
![]()
Контрольная работа №2
№206
Дано:
![]()
Найти: ![]()
Решение
Согласно закону Дальтона и в соответствии с уравнением Менделеева – Клапейрона можем записать
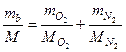
откуда
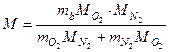
Подставив числовые значения, находим
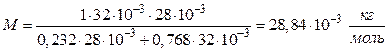
Ответ:
![]()
№216
Дано:
![]()
Найти: ![]()
Решение
Средняя квадратичная скорость определяется как
![]()
Тогда, учитывая условие задачи, можем записать
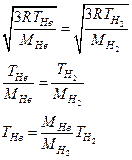
Подставив известные числовые значения, находим
![]()
или
![]()
Ответ:
![]()
№226
Дано:
![]()
Найти: ![]()
Решение
Средняя длина свободного пробега определяется как
![]()
где ![]() - эффективный диаметр молекулы азота.
- эффективный диаметр молекулы азота.
Согласно основному уравнению молекулярно кинетической теории газов
![]()
Откуда концентрация газа равна
![]()
Тогда
![]()
откуда
![]()
Подставив числовые значения, получаем
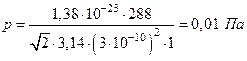
Ответ:
![]()
№236
Дано:
![]()
Найти: ![]()
Решение
Запишем первый закон термодинамики при нагревания газа изобарно
![]()
Изменение внутренней энергии
![]()
где для углекислого газа ![]() .
.
Так как работу газа можно представить в виде
![]()
то получаем
![]()
Тогда имеем
![]()
Откуда находим
![]()
После подстановки значений получаем
![]()
Ответ:
![]()
№246
Дано:
![]()
Найти: ![]()
Решение
В соответствии с уравнением адиабаты имеем
![]()
откуда
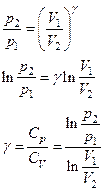
Подставив числове значения, получаем
![]()
Ответ:
![]()
№256
Дано:
![]()
Найти: ![]()
Решение
Изменение энтропии определяется как
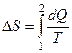
При изохорическом процессе все подводимое количество теплоты идет на изменение внутренней энергии газа
![]()
Тогда
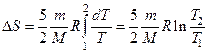
Так как процесс изохорический, то справедливо
![]()
откуда
![]()
Тогда
![]()
Подставив числовые значения, получаем
![]()
Ответ:
![]()
Контрольная работа №3
№306
Дано:
![]()
Найти: ![]()
Решение
Напряженность поля в данном случае, создаваемого бесконечной равномерно заряженной плоскостью, равна
![]()
На заряд действует сила
![]()
где E— напряженность поля, создаваемого зарядом одной пластины. Тогда
![]()
откуда
![]()
Подставив числовые значения, получаем
![]()
Ответ:
![]()
№316
Дано:
![]()
Найти: ![]()
Решение
Напряженность электрического поля на поверхности сферы ( r =R)
![]()
Напряженность электрического поля в центре сферы равна нулю:
![]()
Подставив числовые значения, найдем
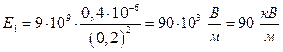
Потенциалы поля заряженного шара радиуса ![]() равен при
равен при ![]() и
и ![]() , т.е. внутри, а значит и в центре, шара, равны и определяются как
, т.е. внутри, а значит и в центре, шара, равны и определяются как
![]()
Подставив числовые значения, найдем
![]()
Ответ:
![]() ;
; ![]() ;
; ![]()
№326
Дано:
![]()
Найти: ![]()
Решение
На электрон, влетевший в электрическое поле, со стороны поля действует сила
![]()
Поскольку напряженность электрического поля направлена вверх, сила, действующая на электрон, направлена вниз. Движение электрона можно рассматривать как суперпозицию двух независимых движений, происходящих в горизонтальном и вертикальном направлениях. В горизонтальном направлении электрон будет двигаться равномерно, так как в этом направлении на него не действуют никакие силы. Одновременно с этим под действием электрической силы он равноускоренно перемещается вниз. Траекторией движения будет парабола.
Поскольку на электрон в вертикальном направлении действует только одна сила ![]() (силой тяжести, действующей на электрон, пренебрегаем), то
(силой тяжести, действующей на электрон, пренебрегаем), то ![]() , где
, где ![]() . Тогда
. Тогда
![]()
откуда
![]()
Угол, на который отклоняется от первоначального направления электрон, равен
![]()
Подставив числовые значения, находим
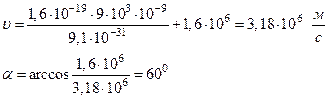
Ответ:
![]()
№336
Дано:
![]()
Найти: ![]()
Решение
Энергия заряженного конденсатора
![]()
Общая емкость последовательно соединенных конденсаторов определяется как
![]()
откуда найдем
![]()
Общая емкость параллельно соединенных конденсаторов определяется как
![]()
Тогда
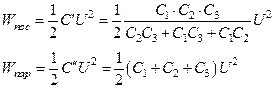
Подставив числовые значения, получаем
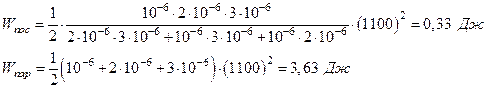
Ответ:
![]()
№346
Дано:
![]()
Найти: ![]()
Решение
При последовательном соединении источников полная ЭДС батареи равна алгебраической сумме ЭДС всех источников, а суммарное сопротивление равно сумме сопротивлений, т.е.
для первой схемы имеем
![]()
А для второй схемы, учитывая соединение источников, получаем
![]()
Согласно закону Ома имеем
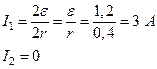
Для первой схемы
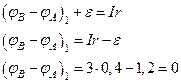
Для второй схемы
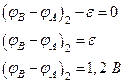
Ответ:
![]()
№356
Дано:
![]()
Найти: ![]()
Решение
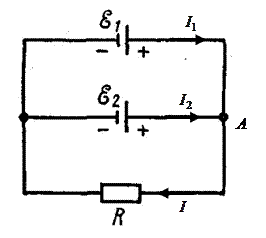 Выбираем направление токов, как показано на рис. Для узла запишем первый закон Кирхгофа
Выбираем направление токов, как показано на рис. Для узла запишем первый закон Кирхгофа
![]()
Для контура ![]() , направление обхода – по часовой стрелке, запишем второе правило Кирхгофа
, направление обхода – по часовой стрелке, запишем второе правило Кирхгофа
![]()
Для контура ![]() , направление обхода – по часовой стрелке, запишем второе правило Кирхгофа
, направление обхода – по часовой стрелке, запишем второе правило Кирхгофа
![]()
Решаем систему уравнений
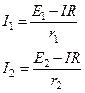
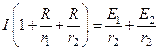
Окончательно получаем
![]()
Подставив числовые значения, находим
![]()
Ответ:
![]()
Похожие работы
-
Физика. Билеты к экзамену за 9 класс
Физика 9 кл. Бровкиной Билет №1 1. Механическое движение. Система отсчета. Материальная точка. Траектория. Путь и перемещение материальной точки. 2. Лабораторная работа. Определение коэффициента трения скольжения.
-
Движение тела под действием силы тяжести
Движение тела по эллиптической орбите вокруг планеты. Движение тела под действием силы тяжести в вертикальной плоскости, в среде с сопротивлением. Применение законов движения тела под действием силы тяжести с учетом сопротивления среды в баллистике.
-
Физические основы явления выстрела
В некотором приближении поведение пороховых газов можно описать с помощью уравнения Менделеева Клапейрона. Это позволяет качественно проанализировать явление выстрела и построить графики зависимости давления газа
-
Физика (7-10 классы)
Магнитная индукция B = F/Il = M/IS, где M – момент сил Справочные таблицы по физике Сила Ампера F = Ibl Сила Лоренца
-
Центр скоростей и ускорение плоскодвижущегося шатуна
Расчет мгновенного центра скоростей и центростремительного ускорения шатуна, совершающего плоское движение. Определение реакции опор для закрепления бруса, при котором Ма имеет наименьшее значение. Нахождение модуля ускорения и модуля скорости точки.
-
Интегрирование уравнений движения материальной точки, находящейся под действием переменных сил
Закон движения груза для сил тяжести и сопротивления. Определение скорости и ускорения, траектории точки по заданным уравнениям ее движения. Координатные проекции моментов сил и дифференциальные уравнения движения и реакции механизма шарового шарнира.
-
Задачи по физике
Заказ №1448 Контрольная по физике. Два велосипедиста выехали из пункта в пункт одновременно. Скорость первого велосипедиста , а скорость второго . Во время движения первый велосипедист был вынужден остановиться в пункте
-
Оптика 2
Федеральное агенство по образованию ГОУ ВПО «Уральский государственный технологический университет – УПИ» Нижнетагильский технологический институт (филиал) УГТУ-УПИ
-
Основная задача механики
Решение задачи на нахождение скорости тела в заданный момент времени, на заданном пройденном пути. Теорема об изменении кинетической энергии системы. Определение скорости и ускорения точки по уравнениям ее движения. Определение реакций опор твердого тела.
-
Основы оптики
Контрольная работа №3 Вариант 19 Задание №28.19 Преломляющий угол θ призмы, имеющей форму острого клина, равен 2°. определить угол наименьшего отклонения σ