Название: Реакция опор твердого тела

Вид работы: контрольная работа

Рубрика: Физика

Размер файла: 163.57 Kb

Скачать файл: referat.me-342877.docx

Краткое описание работы: Порядок определения реакции опор твердого тела, используя теорему об изменении кинетической энергии системы. Вычисление угла и дальности полета лыжника по заданным параметрам его движения. Исследование колебательного движения материальной точки.

Реакция опор твердого тела

Определение реакции опор твердого тела

Дано: Q= 4 кН Т=6 кН G=3 кН a=20 см b=40 см c=15 см R=20 см r=10 см T=2ttIIAY

TAZ PIIAY

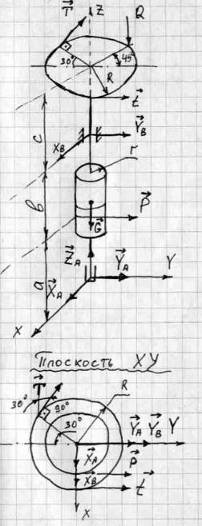
Решение: К системе приложены сила тяжести G, силы натяжения нитей T, t и P. Реакция подпятника А определяется тремя составляющими: XА, YA,ZA, а реакция подшипника В-двумя: Хв и Yв.

Из этих сил – шесть неизвестных. Для их определения можно составить шесть уравнений равновесия.

ΣX=0 XA+XB-Tcos30°= 0 (1)

ΣY=0 YA+YB+Tsin30°+P+t = 0 (2)

ΣZ=0 ZA-G-Q=0 (3)

ΣMAX=0 –YB(a+b)-Pa-QRcos45°-t(a+b+c)-Tsin30°(a+b+c)=0 (4)

ΣMAY=0 XB(a+b)-QRsin45°-Tcos30°(a+b+c)=0 (5)

ΣMAZ=0 Pr+tR-TR=0 (6)

Из уравнения (6) находим P=(T-t)R/r = (6-3)*20/10= 6 кН

Из уравнения (5) находим XB= (QRsin45°+Tcos30°(a+b+c))/(a+b) = (4*20*0,707+6*0,866(20+40+15))/(20+40) = 7,44 кH

Из уравнения (4) находим YB= -(Pa+QRcos45°+t(a+b+c)+Tsin30°(a+b+c))/(a+b) = -(6*20+4*20*0,707+3*(20+40+15)+6*0,5(20+40+15))/(20+40)= -10,44 кH

Из уравнения (3) находим ZA=G+Q=3+4= 7 кH

Из уравнения (2) находим YA=-YB-Tsin30°-P-t=10,4-6*0,5-6-3= -1,6 кН

Из уравнения (1) находим XA=-XB+Tcos30°= -7,44+6*0,866= -2,24 кН

Знак (-) перед найденными значениями реакций XA,YAи YB означает, что данные силы действуют в направлении, противоположном выбранному на рисунке.

Точка М движется относительно тела D . По заданным уравнениям относительного движения точки М и движения тела D определить для момента времени t = t ₁ абсолютную скорость и абсолютное ускорение точки M .

Схема механизма показана на рисунке 1, исходные данные, приведены в таблице 1:

Уравнение относительного движения точки М ОМ= Sr = Sr ( t ),см.	Уравнение движения тела φ e = φ e ( t ), рад	t1 , c	α , град
6( t+0,5t2 )	t3 -5t	2	30

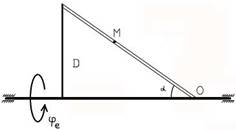
Рисунок 1

Решение

Будем считать, что в заданный момент времени плоскость чертежа совпадает с плоскостью треугольника D . Положение точки М на теле D определяется расстоянием S_r =ОМ.

При t = 2 c

S_r =6(2+0,5*2² ) = 24 см.

Абсолютную скорость точки М найдём как геометрическую сумму относительной и переносной скоростей:

Модуль относительной скорости

,

где

.

При t = 2 c

Положительный знак у показывает, что вектор направлен в сторону возрастания S_r .

(1)

где R – радиус окружности L, описываемый той точкой тела, с которой в данный момент совпадает точка M , R = S_r sin 30 ⁰ = 12 см; - модуль угловой скорости тела:

При t = 2 c

Положительный знак у величины показывает, что вращение треугольника происходит вокруг оси OY в сторону, направления отчёта угла α. Поэтому вектор направлен по оси OY влево Рисунок 2.

Модуль переносной скорости, по формуле (1),

Вектор направлен по касательной к окружности L в сторону вращения тела. Так как и взаимно перпендикулярны, модуль абсолютной скорости точки M

,

или

Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений:

или в развёрнутом виде

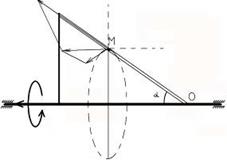
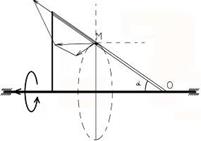
Рисунок 2 Рисунок 3

Модуль относительного касательного ускорения

где

При t = 2 c

Положительный знак показывает, что вектор направлен в сторону S_r . Знаки и одинаковы; следовательно, относительное движение точки М ускоренное.

Относительное нормальное ускорение

так как траектория относительного движения – прямая ().

Модуль переносного вращательного ускорения

(2)

где - модуль углового ускорения тела D :

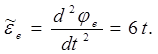
При t = 2 c

Знаки и одинаковы; следовательно, вращение треугольника D ускоренное, направления векторов и совпадают Рисунок 2,3.

Согласно (2),

Вектор направлен в ту же сторону, что и .

Модуль переносного центростремительного ускорения

Вектор направлен к центру окружности L .

Кориолисово ускорение

Модуль кориолисова ускорения

где

С учётом найденных выше значений, получаем

Вектор направлен согласно правилу векторного произведения Рисунок 3

Модуль абсолютного ускорения точки М находим способом проекций:

Результаты расчёта сведены в таблице 2.

	Скорость, см/с				Ускорение, см/с2
7	84	18	85,9	12	588	144	0	6	126	270		-591	649

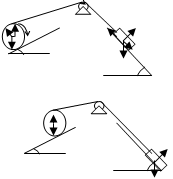Д-10 вар.8 d

Дано ω

m₁ =mA

m₂ =1/2m R N ω FтрN

m₃ =1/3m G δ

R₃ =30 p 30⁰ G

α=30⁰

β=45⁰ 45⁰

f=0.15 Рис №1

δ=0.20см d

S=1.75м А

Найти v₁ N

G

р

N

G

Применим теорему об изменении кинетической энергии системы:

(1)

где и кинетические энергии системы в начальном и конечном положениях; сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное; сумма работ внутренних сил системы на том же перемещении.

Для рассматриваемой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями.

Так как в начальном положении система находится в покое, то .

Следовательно, формула (1) принимает вид.

(2)

Найдем кинетические энергии тел участвующих в системе.

Найдем кинетическую энергию тела 1 движущегося поступательно

(3)

Найдем кинетическую энергию тела 2 вращающегося вокруг оси Ox

(4)

Момент инерции относительно оси вращения.

(5)

Так как точка Р является мгновенным центром скоростей, то 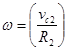и следовательно,

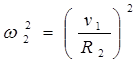(6)

Подставив в формулу (4) формулы (5) и (6) получим кинетическую энергию тела 2 вращающегося вокруг оси Ox:

(7)

Найдем кинетическую энергию тела 3 совершающего плоско вращательное движение

(8)

(9)

Так как точка Р является мгновенным центром скоростей, то 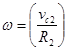и следовательно,

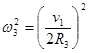(10)

Подставив в формулу (8) формулы (9) и (10) получим кинетическую энергию тела 3 совершающего плоско вращательное движение:

(11)

Теперь полученные формулы (3), (7) и (11) подставим в формулу вида

и получим формулу суммы кинетических энергий для данной системы имеющий вид:

(12)

Найдем сумму работ всех внешних сил, приложенных к системе, на заданной ее перемещении.

Работа силы тяжести

(13)

Работа силы трения

(14)

(15)

при подстановки в формулу (14) формулу (15) работа силы трения имеет вид

(16)

Работа силы тяжести

(17)

Работа силы сцепления катка 2 равна нулю, так как эта сила приложена в мгновенный центр скоростей этого катка.

Работа пары сил сопротивления качению катка 3

(18)

(19)

(20)

при подстановки в формулу (19) формулы (20) момент инерции имеет вид

(21)

(22)

при подстановки в формулу (18) формул (21) и (22) работа пары сил сопротивления качению имеет вид.

(23)

для нахождения общей работы воспользуемся формулой такой и теперь подставим в неё формулы (13), (16), (17) и (23) получим.

(24)

примем за величину которая в скобках получим

(25)

подставим в выражение (24) уравнение (25) и получим

(26)

воспользовавшись формулой (2) и подставив, туда формулы (12) и (26) получим

(27)

подставив в формулу (27) выражение (25) получим

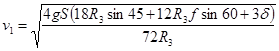
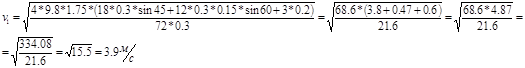
ответ;

Р₁ =6кН

Р₂ =6кН

q=1кН/м

M=7кН*м

Q=q*10=10кН

1) X_c -?

Q*dt_c -p₁ cos*dt_c -p₂ cos+dt_c +X_c *dt_c =0

X_c +Q-p₁ cos-p_2c os=0

X_c =p₁ cos+p₂ cos-Q/1=6*cos+6*cos-10=1,84кН;

2) Y_c -?

Mdj_AD -Q*10dj_AD +Y_c *5dj_B -p₂ *3sin*dj_BC +p₂ *3sin*dj_BC +p₁ cos*dj_BC =0

dj_AD -dj_BC

M-Q*10+Y_c *5-p₂ *3sin+p₁ *3sin+p₁ *5cos/5=-7+10*10+6*3*0,86-6*3*0,5-6*5*0,86/5=14,7 кН;

Q-p₁ cos-p₂ cos-X_c= 0

10-6*0,86-6*0,5-1,8=0

R_A -R_B -p₁ sin-p₂ sin-Y_c =0 (R_A =7,15; R_B =13,69)

7,15-13,69-8,16+14,7=0

Исходные данные

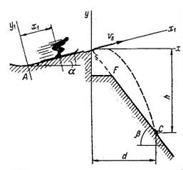
Лыжник подходит к точке A участка трамплина AB, наклонённого под углом α к горизонту и имеющего длину l, со скоростью V_A . Коэффициент трения скольжения лыж на участке AB равен f. Лыжник от точки A до точки B движется τ с. В точке B со скоростью V_B он покидает трамплин. Через T с. лыжник приземляется со скоростью V_C в точке C горы, составляющей угол β с горизонтом.

VA , м/с	VB , м/с	τ, с	β, º	f
21	20	12	60	0

Найти

По заданным параметрам движения точки определить угол α и дальность полёта d.

Решение.

1. Рассмотрим движение лыжника на участке AB. Принимая его за материальную точку, покажем действующие на него силы. Так как коэффициент трения равен нулю, то сила трения отсутствует, следовательно, на точку действует только сила тяжести G.

Пусть масса точки равна m, тогда составим уравнение движения точки на участке AB.

Интегрируя данное дифференциальное уравнение дважды, получаем:

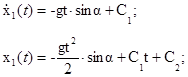
Для определения постоянных интегрирования воспользуемся начальными условиями: при t₁ =0 с:

Таким образом, имеем:

То есть уравнения движения точки примут вид:

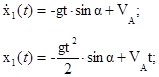
Для момента τ, когда точка покидает участок AB, , то есть имеет место равенство . Отсюда искомый угол равен:

2. Составим дифференциальные уравнения движения точки вдоль осей координат на участке BC.

Проинтегрируем дифференциальные уравнения дважды:

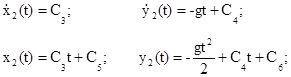
Начальные условия данной задачи при t₂ =0 c:

Согласно начальным условиям получаем, что:

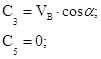
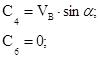
Получили, что проекции скорости точки на оси координат равны:

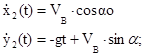
а уравнения её движения вдоль осей имеют следующий вид:

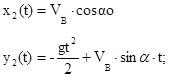
Так как в точке C скорость точки направлена под углом β к горизонту, то скорость точки вдоль оси y₂ равна:

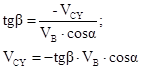
В то же время известно, что .

Следовательно, время движения лыжника на участке DC равно:

с.

Таким образом, дальность прыжка лыжника равна:

м.

Результаты расчётов

α, º	d, м
20	75,52

Исследование колебательного движения материальной точки

Две параллельные пружины 1 и 2, имеющие коэффициенты жесткости с₁ =4 Н/см и с₂ =6 Н/см, соединены абсолютно жестким брусом AB, к точке K которого прикреплена пружина 3 с коэффициентом жесткости с₃ =15 Н/см. Точка K находится на расстояниях a и b от осей пружин 1 и 2: a/b=c₂ /c₁ . Пружины 1, 2 и 3 не деформированы. Груз D массой 2,5 кг. Присоединяется к концу N пружины 3; в тот же момент грузу D сообщают скорость , направленную вниз параллельно наклонной плоскости (). Массой бруска AB пренебречь.

Дано:

Найти: уравнение движения груза D.

Решение

1) Находим приведенную жесткость пружин:

; ;

Для определения f_{с m} составим уравнение, соответствующее состоянию покоя груза D на наклонной плоскости:

; ;

Дифференциальное уравнение движения груза примет вид:

; ;

Постоянные С₁ и С₂ определяем из начального условия:

при t=0; x₀ =-f_{cm ;}

Уравнение движения груза имеет следующий вид:

Найдем числовые значения входящих в уравнение величин

Следовательно, уравнение движения груза D:

Ответ: