Название: Определение реакции опор твёрдого тела

Вид работы: контрольная работа

Рубрика: Физика

Размер файла: 355.77 Kb

Скачать файл: referat.me-343378.docx

Краткое описание работы: Рассчётно -графическая работа С-7 «Определение реакции опор твёрдого тела» Cилы, кН Размеры, см Результаты вычислений приведены в таблице: Силы, кН

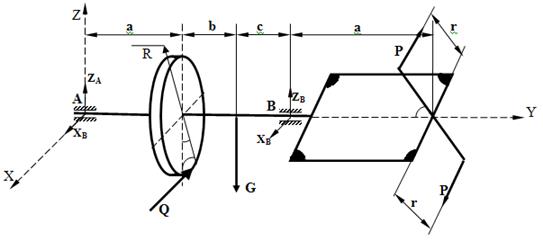
Определение реакции опор твёрдого тела

Рассчётно-графическая работа С-7

«Определение реакции опор твёрдого тела»

Cилы, кН		Размеры, см
Q	G	a	b	c	R	r
5	3	20	15	10	30	40

60º

90º

45º

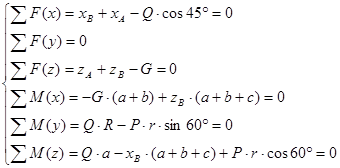
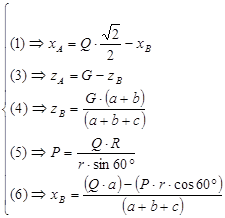
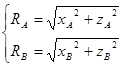
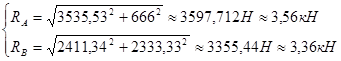
Результаты вычислений приведены в таблице:

Силы, кН
RA	RB	xA	zA	xB	zB
3,56	3,36	3,53	0,67	-2,41	2,33

При нахождении получилось, что значение составляющей по оси отрицательно. Это значит, что при расставлении действующих на данную систему сил было выбрано неверное направление. В итоге правильное построение будет выглядеть следующим образом:

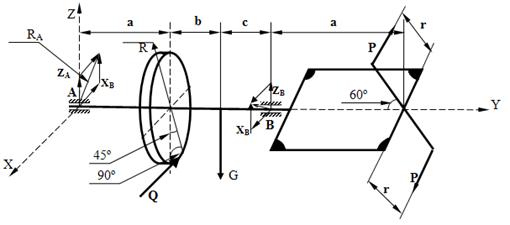
«Определение скорости и ускорения точки по заданным уравнениям её траектории».

Уравнения движения		t1 ,c
x=x(t)	y=y(t)
		2

1. Скорость

В общем случае для пространственной системы координат будем иметь:

=>

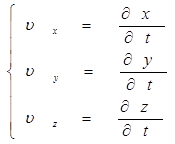Для нашего случая уравнения для составляющих по осям координат будут иметь следующий вид:

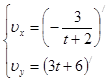
После дифференцирования получим:

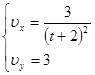
Найдём полную скорость точки в момент времени :

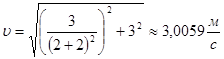
2. Ускорение

В общем случае для пространственной системы координат будем иметь:

=>

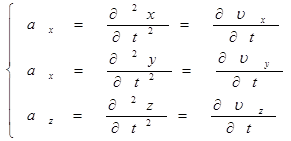Для нашего случая уравнения для составляющих по осям координат будут иметь следующий вид:

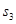
После дифференцирования получим:

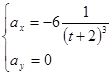
Найдём полное ускорение точки в момент времени :

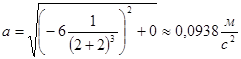
С другой стороны ускорение можно найти по формуле:

, где

тангенциальное ускорение (касательная составляющая полного ускорения), а нормальная составляющая полного ускорения, которые можно найти по формулам:

,

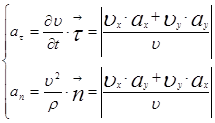где - радиус кривизны траектории в искомой точке.

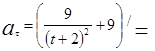-0,0058 при =2 с.

Тогда найдётся по формуле:

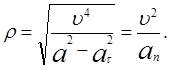
Подставив значения, получим:

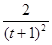
Найдём уравнение движения точки. Для этого выразим из второго уравнения переменную времени () и подставим полученное выражение в первое уравнение:

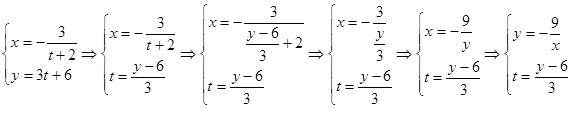
Получившееся уравнение () является гиперболой.

Найдём начальное положение точки. Для этого подставим в уравнения значение .

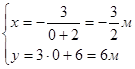
Чтобы определить в какую сторону происходит движение необходимо подставить в уравнение движения время, отличное от (например ).

движение происходит по левой ветви гиперболы в направлении, указанном на рисунке.

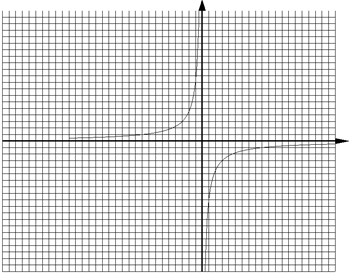
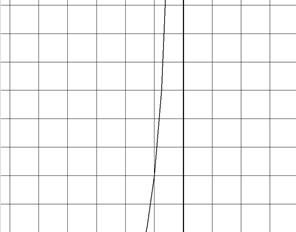
Расставим на графике движения векторы скорости, ускорения и векторы полной скорости и ускорения:

,	,	,	,	,	,	,	,	,
0,1875	3	3,0059	-0,0938	0	-0,0058	0,094	0,0938	96,12

Дано:

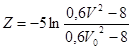
m₁ = m

m₂ = 2m

m₃ = 9m

R₃ = 0,3 м

i_3ξ = 0,2 м

α = 30

f = 0,12

δ = 0,25 см

s = 1,5 м

Найти :

V ₁ = ?

Решение:

По теореме об изменении кинетической энергии системы:

(т.к. система состоит из абсолютно твердых тел и нерастяжимых нитей)

Кинетическая энергия системы равна:

Сумма работ внешних сил:

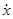
м/с

Интегрирование дифференциальных уравнений

Д-1 вар. 9

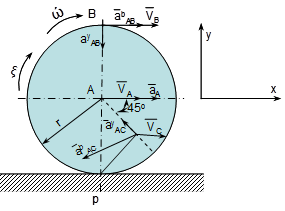
Лыжник

Vв

h

d

Дано

a=15° ; ; ƒ=0,1 τ=0,3 ;β=45α

h=42 β

Найти Va, Vв

Решение

mX=SXi 1 Fтр=fN

mX=Gsina-Fcoпр N=Gcosa

a

mX=Gsina-fGcosa

X=gsina-fgcosa

X=(g(sina-fcosa) t+ C₁

X=(g(sina-fcosa)/2) t² + C₁ t+ C₂

При нормальных условиях : t=0 x=0

X=Vв X= C₂ =0; C₁ =Va

X=g (sina-fcosa) t+ C₁ X= (g (sina-fcosa)/2) t² +С₁ *t

X=VвX=L

Vв=g (sinα-ƒ*cosα)τ+Va2

L= ((g(sinα-ƒ*cosα)τ)/2)τ+С₁ *t

Рассмотрим движение лыжника от точки В до точки С, составим дифференциальное уравнение его движения.

Mx=0 my=0

Начальные условия задачи: при t=0

X0=0 Y0=0

X0=Vв*cosα ; Y0=Vв*sinα

Интегрируем уравнения дважды

Х=C3 Y=gt+C4 2

X= C3t+ C5 Y=gt /2+C4t+C6

при t=0

X=C3; Y0=C4

X=C5; Y0=C6

Получим уравнения проекций скоростей тела.

X=Vв*cosα , Y=gt+Vв*sinα

и уравнения его движения

X=Vв*cosα*tY=gt /2+Vв*sinα*t

Уравнение траектории тела найдем , исключив параметр tиз уравнения движения получим уравнение параболы.

Y=gx/2(2Vв*cosα) + xtgα

Y=hx=dh=tgβ*dd=h/tgβ

Найдём Vв из уравнения 2 2 2

Y=gx/2(2Vв*cosα) + xtgα

Vв=18м/с и найдём Va

Vв=g(sinα-ƒ*cosα)τ+Va

Va=11,3м/с

Ответ: Va=11,3м/с Vв=18м/с

Задание Д.3

Исследование колебательного движения материальной точки

Дано:

Найти: Уравнение движения

Решение:

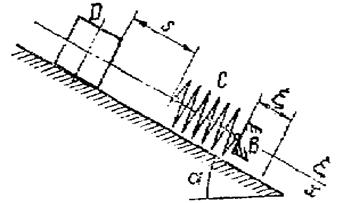
Применим к решению задачи дифференциальное уравнение движения точки. Совместим начало координатной системы с положением покоя груза, соответствующим статической деформации пружины, при условии что точка В занимает свое среднее положение . Направим ось вниз вдоль наклонной плоскости. Движение груза определяется по следующему дифференциальному уравнению:

,

где -сумма проекций на ось сил, действующих на груз.

Таким образом

Здесь ,

где - статическая деформация пружины под действием груза; -перемещение точки прикрепления нижнего конца пружины, происходящее по закону .

Статическую деформацию пружины найдем из уравнения, соответствующего состоянию покоя груза:

т.е.

Откуда

Дифференциальное уравнение движения груза примет вид:

или после преобразования

Разделив все члены уравнения на получим:

Введем обозначения:

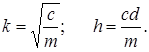
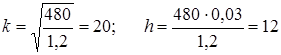
Получаем, что

Имеем неоднородное уравнение

,

где - общее решение, соответствующего однородного уравнения;

- частное решение данного неоднородного уравнения.

Общее решение однородного уравнения имеет вид:

Частное решение неоднородного уравнения:

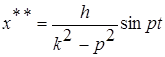
Общий интеграл

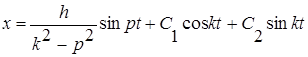
Для определения постоянных интегрирования найдем, кроме ого, уравнение для :

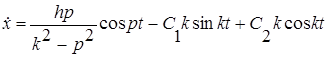
и используем начальные условия задачи.

Рассматриваемое движение начинается в момент , когда деформация пружины является статической деформацией под действием груза.

Таким образом, при

Составим уравнения и для :

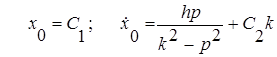
Откуда

Тогда уравнение движения груза примет вид:

Ответ:

Применение теоремы об изменении количества движения к исследованию движения механической системы.

Дано:

Найти: Скорость .

Решение:

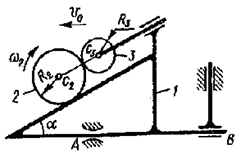
На механическую систему действуют внешние силы: - сила сухого трения в опоре А; - силы тяжести тел 1, 2 и 3; -сила нормальной реакции в точке А; -реактивный момент в опоре В.

Применим теорему об изменении количества движения механической системы в дифференциальной форме. В проекциях на оси координат

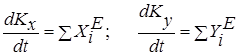, (1)

где - проекции вектора количества движения системы на оси координат; - суммы проекций внешних сил на соответствующие оси.

Количество движения системы тел 1, 2 и 3

(2)

где

. (3)

Здесь - скорости центров масс тел 1, 2, 3; - соответственно переносные и относительные скорости центров масс.

Очевидно, что

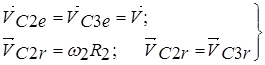(4)

Проецируя обе части векторного равенства (2) на координатные оси, получаем с учетом (3) и (4)

(5)

где - проекция вектора на ось ;

Проекция главного вектора внешних сил на координатные оси

(6)

Знак « - » соответствует случаю, когда , а знак «+» - случаю, когда .

Подставляя (5) и (6) в (1), получим

(7)

Выразим из второго уравнения системы (7) величину нормальной реакции и подставим ее в первое уравнение. В результате получим

при ; (8)

при . (9)

где

Рассмотрим промежуток времени , в течении которого тело 1 движется вправо . Из (8) следует, что

,

где С- постоянная интегрирования, определяемая из начального условия: при

.

При скорость тела 1 обращается в ноль, поэтому .

Найдем значения и :

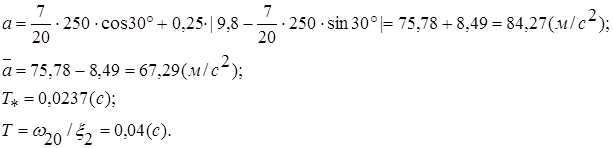
Т.е. , . Значит, тело при начинает двигаться в обратном направлении. Это движение описывается дифференциальным уравнением (9) при начальном условии: ; (10)

Интегрируя (9) с учетом (10), получим, при

(11)

При получим из (11) искомое значение скорости тела 1 в момент, когда

.

Точное решение задачи. Воспользовавшись методикой, изложенной выше, получим дифференциальное уравнение движения тела 1:

при (12)

; при , (13)

где

Из (12) и учитывая, что получаем, при

откуда 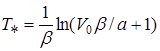или

Из (13) и учитывая, что получаем, при

При находим

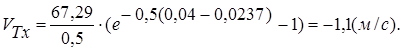
Ответ :.