Referat.me
/ / Решение задачи с помощью программ Mathcad и Matlab

Название: Решение задачи с помощью программ Mathcad и Matlab

Вид работы: контрольная работа

Рубрика: Информатика и программирование

Размер файла: 57.67 Kb

Скачать файл: referat.me-134213.docx

Краткое описание работы: Исследование связи между временем достижения торпеды, снабжённой разгонным двигателем (глубинной бомбы) заданной глубины и формой корпуса противолодочного корабля: сферической, полусферической, каплевидной. Представление этой зависимости графически.

Решение задачи с помощью программ Mathcad и Matlab

Контрольная работа

Решение задачи с помощью программ Mathcad и Mat l ab

Содержание

Текст задания

1. Тексты программ в среде MathCAD

2. Тексты программ в среде Matlab


Задание

Глубинная бомба – торпеда, снабжённая разгонным двигателем, установленная на взрыв на заданной глубине, сбрасывается со стоящего неподвижно противолодочного корабля. Исследовать связь между временем достижения заданной глубины и формой корпуса (сферической, полусферической, каплевидной и т.д).


1. Тексты программ в среде MathCAD

Часть 1:

Шар:

- масса бомбы

- ускорение свободного падения

- площадь поперечного сечения тела

- плотность среды

- скорость падения бомбы


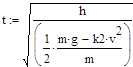
- время, через которое бомба достигнет заданной глубины 400 м.

Часть 2:

Полусфера:

- масса бомбы

- ускорение свободного падения

- площадь поперечного сечения тела

- плотность среды

- скорость падения бомбы


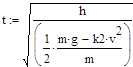
- время, через которое бомба достигнет заданной глубины 400 м.

Часть 3:

Каплевидное тело:

- масса бомбы

- ускорение свободного падения

- площадь поперечного сечения тела

- плотность среды

- скорость падения бомбы

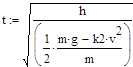
- время, через которое бомба достигнет заданной глубины 400 м.

2. Тексты программ в среде Matlab

Часть 1 (шар):

Текст программы:

hold on;

grid on;

c=0.4;

m=50;

g=9.81;

S=2;

p=1;

V=20;

t=0:0.5:14;

k2=0.5*c*S*p;

h=0.5.*((m*g-k2*V^2)*(t.^2))/m;

plot(t,h);

title('Grafik');

xlabel('t');

ylabel('h');

График:


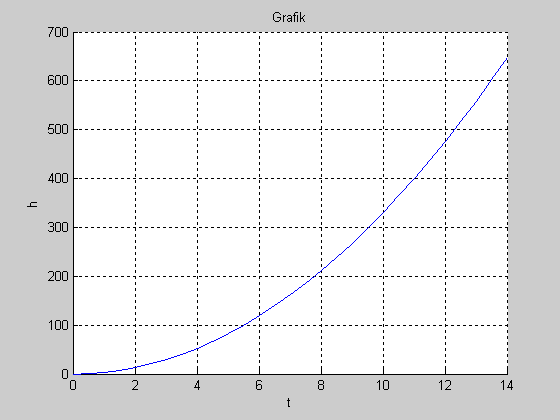
Часть 2 (полусфера):

Текст программы:

hold on;

grid on;

c=0.55;

m=50;

g=9.81;

S=2;

p=1;

V=20;

t=0:0.5:14;

k2=0.5*c*S*p;

h=0.5.*((m*g-k2*V^2)*(t.^2))/m;

plot(t,h);

title('Grafik');

xlabel('t');

ylabel('h');

График:

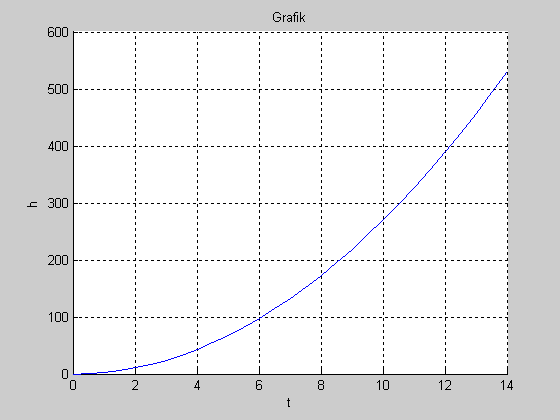
Часть 3 (каплевидное тело):

Текст программы:

hold on;

grid on;

c=0.045;

m=50;

g=9.81;

S=2;

p=1;

V=20;

t=0:0.5:10

k2=0.5*c*S*p;

h=0.5.*((m*g-k2*V^2)*(t.^2))/m;

plot(t,h);

title('Grafik');

xlabel('t');

ylabel('h');

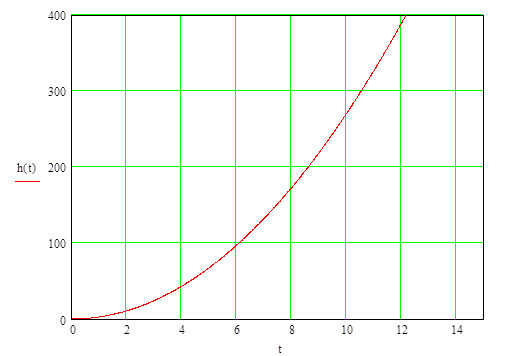
График:

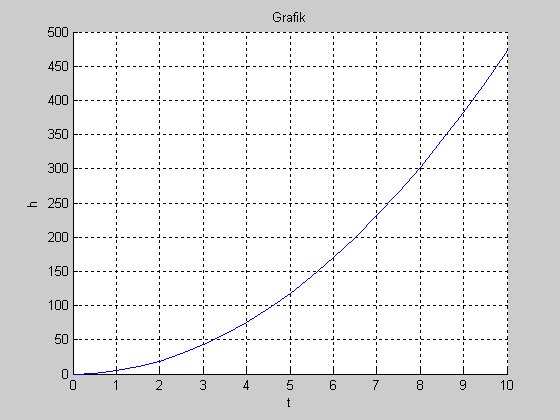
Похожие работы

  • Вычисление значения функции y(x)

    Особенности применения компьютерных программ Pascal, Excel, MathCAD и Delphi для вычисления значения функции y(x) с заданным промежутком и шагом. Виды результатов вычислений, их сравнение и вывод. Изображение блок-схемы алгоритма решения задания.

  • Дослідження перехідних характеристик цифрових САК

    Дослідження цифрових систем автоматичного керування. Типові вхідні сигнали. Моделювання цифрової та неперервної САК із використання MatLab. Результати обчислень в програмі MatLab. Збільшення періоду дискретизації цифрової системи автоматичного керування.

  • ЭВМ с использованием математического пакета MathCad в среде Windows 98 для решения дифференциального уравнения n-го порядка

    Решение дифференциального уравнения N-го порядка методом интегрирования при помощи характеристического уравнения, методом интегрирования и операторным методом для значений аргументов при заданных начальных условиях и нулевых уравнения 4–го порядка.

  • Оптимальное распределение неоднородных ресурсов

    Определение оптимального плана производства продукции при наличии определенных ресурсов, проблемы оптимизации распределения неоднородных ресурсов на производстве с помощью системы символьной математики Mathcad. Составление алгоритма симплекс-метода.

  • Одномерная оптимизация функций методом золотого сечения

    Создание программы в среде программирования MatLab для решения задачи одномерной оптимизации (нахождение минимума и максимума заданных функций) методом золотого сечения, построение блок-схемы алгоритма и графическое изображение исследованных функций.

  • Mathcad и MAS – что это такое

    Mathcad создавался как программное средство, альтернативное электронным таблицам. И не электронным таблицам современным, а тем, какие были на момент создания первых версий Mathcad.

  • Моделирование структурных схем в среде SIMULINK пакета MATLAB

    Практические навыки моделирования структурных схем в среде SIMULINK пакета MATLAB. Построение графиков функций в декартовой системе координат. Решение систем линейных и нелинейных уравнений. Работа с блоками Sum, Algebraic Constraint, Gain, Product.

  • Моделирование движения невесомой заряженной частицы в электрическом поле в среде MathCAD и Matlab

    Моделирование движения невесомой заряженной частицы в электрическом поле, созданном системой нескольких фиксированных в пространстве заряженных тел, в случае, когда заряженные тела находятся в одной плоскости и в ней же находится движущаяся частица.

  • Дискретное преобразование Фурье

    Разработка функции вычисления дискретного преобразования Фурье от входного вектора. Исследование свойств симметрии ДПФ при мнимых, четных и нечетных входных сигналах. Применение обратного преобразования Фурье для генерации периодической функции косинуса.

  • Інженерні розрахунки в MathCad

    Розв’язання системи лінійних та нелінійних рівнянь у програмі MathCAD. Матричний метод розв'язання системи рівнянь. Користування панеллю інструментів Математика (Math) для реалізації розрахунків в системі MathCAD. Обчислення ітераційним методом.