Название: Графический метод решения задач линейного программирования
Вид работы: контрольная работа
Рубрика: Информатика и программирование
Размер файла: 31.32 Kb
Скачать файл: referat.me-135042.docx
Краткое описание работы: Расчет производства необходимого количества продукции для получения максимальной прибыли предприятия. Математическая модель для решения задач линейного программирования. Построение ограничений и целевых функций. Исследование чувствительности модели.
Графический метод решения задач линейного программирования
Министерство науки и образования Украины
Днепропетровский Национальный Университет
Факультет электроники, телекоммуникаций и компьютерных систем
Кафедра автоматизированных систем обработки информации
Расчётная работа №1
Графический метод решения задач линейного программирования
Выполнил: ст. гр. РС-05,
Паляруш А.Б.
Проверил:
Доцент кафедры АСОИ
Саликов В.А
Г. Днепропетровск
2007 г.
Постановка задачи
Для производства двух видов продукции А и В предприятие использует 4 группы оборудования (1, 2, 3, 4) на производство одной штуки продукции А требуется занять в течение рабочей смены 1, 0, 5 и 3 единиц соответственно 1, 2, 3, 4 оборудования, а на производство одной штуки продукции В требуется 1, 1, 0, 2 единиц оборудования 1, 2, 3, 4. Имеется оборудование по группам 1 – 18, 2 – 12, 3 – 24, 4 – 18 единиц. Предприятие получает с одной штуки продукции А 4 гривны чистого дохода и 6 гривен - с одной штуки продукции В.
Сколько штук продукции каждого вида должно производить предприятие, чтобы получить наибольшую прибыль?
| Группа оборудования, штук для производства единицы продукции | Прибыль, грн | ||||
| 1 | 2 | 3 | 4 | ||
| А | 1 | 0 | 5 | 3 | 4 |
| В | 1 | 1 | 0 | 2 | 6 |
Построение математической модели
Для реализации графического метода решения задач линейного программирования необходимо определить целевую функцию:
Z=4*x1+6*x2, где Z→max – целевая функция,
x1 – количество изготовленной продукции вида А,
x2 – количество изготовленной продукции вида В.
Далее необходимо определить ограничения, задающие ОДР:
(1) x1+ x2 ≤ 18; вытекает из доступного количества оборудования первой группы
(2) x2 ≤ 12; вытекает из доступного количества оборудования второй группы
(3) 5*x1 ≤ 24; вытекает из доступного количества оборудования третей группы
(4) 2*x1+2*x2 ≤ 18;вытекает из доступного количества оборудования четвёртой группы
(5) x1 ≥ 0;условие неотрицательности;
(6) x2 ≥ 0 ; условие неотрицательности;
Построим все полученные ограничения и целевую функцию:
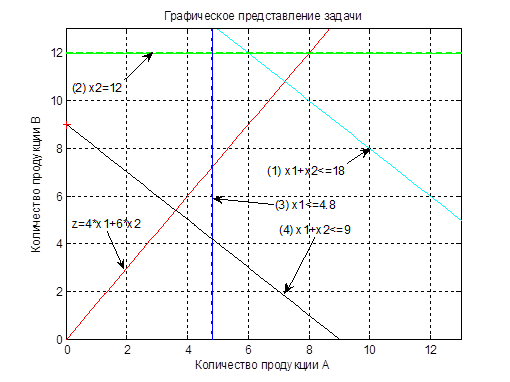
Теперь можно увидеть, что ОДР ограничена (4) x1+x2 ≤ 9, (3) x1 ≤ 4.8, x1 ≤ 0, x2≤ 0.
Наилучшее (оптимальное) решение отмечено красным крестиком. Максимальная прибыль достигается в точке (0, 9), А=0, В=9; при нахождении оптимального решения данной задачи следует помнить, что количество продукции (равно как и количество ресурса) целое число.
Z(0,9)=4*0+9*6=54 (грн).
Чувствительность модели
Благодаря исследованию чувствительности модели, мы получаем информацию о ценности ресурса.
Оборудование группы 1 (голубой цвет на графике) не является дефицитным и не влияет на оптимальную точку т.к. вышло далеко за ОДР, его очень много. Это оборудование станет дефицитным при уменьшении его количества на 9 единиц.
Оборудование группы 2 (зелёный цвет на графике) так же не является дефицитным, однако, при уменьшении его количества на 3 единицы оно начнёт влиять на результат.
Оборудование группы 3 (синий цвет на графике) не дефицитно. Изменяя его количество, при неизменном количестве других ресурсов, мы не повлияем на результат т.к. для производства продукции А (именно она должна производиться для максимальной прибыли) его расход равен 0.
Оборудование группы 4 (чёрный цвет на графике) является дефицитным, ценность данного ресурса можно определить, увеличив его количество на 2 единицы (т.к. именно столько необходимо для производства одной единицы продукции А):
![]()
Следовательно, при изменении количества ресурса 4 на единицу прибыль растёт на 3 гривны. Данный ресурс можно увеличивать до 24 единиц, потом он перестанет быть дефицитным, значит, не будет влиять на оптимальное решение.
Похожие работы
-
Методы решения задач линейного программирования с n-переменными
Характеристика основных методов линейного программирования с n- переменными, в частности, графического и симплекс-метода. Способы решения задачи по определению оптимальной структуры товарооборота, обеспечивающей торговому предприятию максимум прибыли.
-
Симплекс метод решения задачи линейного программирования
Описание симплекс метода решения задачи линейного программирования. Решение задачи методом Литла на нахождение кратчайшего пути в графе, заданном графически в виде чертежа. Из чертежа записываем матрицу расстояний и поэтапно находим кратчайший путь.
-
Табличный симплекс-метод
Математическое программирование. Табличный симплекс – метод. Метод искусственного базиса. Формирование целевой функции и системы ограничений. Статус ресурсов.
-
Исследование устойчивости, решение задач линейного программирования графическим способом
Строение системы уравнений-ограничений и ее переменных, графический способ решения задач линейного программирования на плоскости. Выражение неизвестных через две независимые переменные, являющиеся координатными осями графика. Значение целевой функции.
-
Решение задач линейного программирования симплекс-методом
Сущность линейного программирования. Математическая формулировка задачи ЛП и алгоритм ее решения с помощью симплекс-метода. Разработка программы для планирования производства с целью обеспечения максимальной прибыли: блок-схема, листинг, результаты.
-
Расчет необходимого количества закупаемого сырья с помощью средств Excel и VBA
Определение количества закупаемого сырья на выпуск продукции по месяцам, в течении года и за год в целом. Алгоритм необходимых действий, представление результатов в графическом виде. Решение задачи в табличном процессоре Excel и с помощью средств VBA.
-
Нахождение оптимальных планов производства продукции и их экономико-математический анализ
Решение аналитической задачи с помощью ПЭВМ.
-
Регрессионные зависимости
Вычисление значений регрессионно-авторегрессионной зависимости заданного выражения линейного программирования. Графическое представление математической модели в виде уравнения регрессии. Принципи оптимизации производственных и коммерческих операций.
-
Математическое программирование
Решение задачи линейного программирования симплекс-методом. Нахождение оптимального плана по критерию максимума прибыли. Транспорт - определение плана перевозок грузов на предприятие, которое обеспечивает минимальные совокупные транспортные издержки.
-
Исследование операций
Математическая модель задачи. Система ограничений. Составление симплекс-таблиц. Разрешающий элемент. Линейное программирование. Коэффициенты при свободных членах. Целевая функция. Метод потенциалов, северо-западного угла. Выпуклость, вогнутость функции.