Referat.me
/ / Розв’язання нелінійних диференційних рівнянь методом січних і половинного ділення

Название: Розв’язання нелінійних диференційних рівнянь методом січних і половинного ділення

Вид работы: курсовая работа

Рубрика: Информатика и программирование

Размер файла: 58.17 Kb

Скачать файл: referat.me-137220.docx

Краткое описание работы: Графічне зображення методу половинного ділення. Вибір методу інструментальних засобів вирішення задач. Розробка логічної частини програми для розв’язання нелінійного рівняння методами половинного ділення та січних. Особливість кодування на мові Паскаль.

Розв’язання нелінійних диференційних рівнянь методом січних і половинного ділення

Зміст

1.Загальні відомості

2.Вибір методу інструментальних засобів вирішення задач

3.Функціональне призначення програми

4.Розробка та опис логічної частини програми

5.Керівництво оператору

6.Результати обчислень

Висновки

Література

Додаток А. Блок-схема алгоритму

Додаток Б. Лістинг програми


Анотація

В даній курсовій роботі проведено дослідження двох чисельних методів вирішення нелінійних рівнянь: половинного ділення та січних. Дослідження проводиться на прикладі заданого нелінійного рівняння. Дається опис кожного з методів та задачі в цілому.


1. Загальні відомості

Метод половинного ділення

В цьому методі спочатку обчислюється значення функції в точках, що розташовані через рівні інтервали на осі . Коли імають протилежні знаки, знаходять Якщо знак збігається зі знаком, то надалі замість хп використовується . Якщо жмає знак, протилежний знакові, тобто збігається зі знакомто на замінюється Відзначимо, що і в цьому, і в наступних методах за умову припинення ітераційного процесу доцільно брати умовуде - задана похибка знаходження кореня.

Графічне зображення методу подане на рисунку 1, а структура алгоритму в Додатку А.

Похибка розв'язку через ітерацій знаходиться в межах

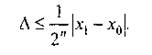
Метод має малу швидкість збіжності, оскільки інтервал, де знаходиться корінь, з кожним кроком зменшується не більше ніж в два рази.

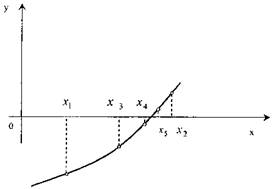
Рис. 1. Метод половинного ділення

Метод січних

Однією з головних проблем при застосуванні методу Ньютона є необхідність аналітичного опису похідної. Якщо це складно чи неможливо, то можна застосувати її наближену оцінку (рисунок 2). Тоді замість методу дотичних застосовується метод січних, за яким

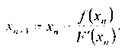
де- наближена оцінка похідної, що розглядається як січна, а не як дотична, і може бути оцінена за формулою

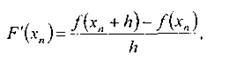
Чи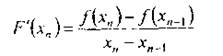

де h — деякий невеликий крок.

Алгоритм цього методу подібний методу Ньютона, але з іншою ітераційною формулою.

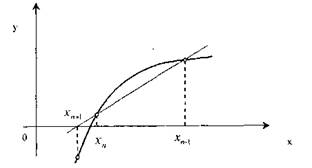
Рис. 2. Метод січних


2. Вибір методу інструментальних засобів вирішення задач

Розв’язок даної задачі реалізовано на ЕОМ, причому було складено алгоритм та програму в середовищі Borland Delphi 7. Програма є досить простою та зрозумілою для користувача середнього рівня. Готову програму можна використовувати навіть на мінімальних системних параметрах процесора типу Intel P-100, 8 Мb ОЗУ та операційній системі MS-Windows 95.

3. Функціональне призначення

Розроблена програма дозволяє розв’язати вказане нелінійне рівняння методами половинного ділення та січних, порівняти результати їх роботи:

,

Результати виводяться у текстовій формі.

4. Розробка та опис логічної частини програми

В даній курсовій роботі було розроблено програмне забезпечення для розв’язання та дослідження заданого нелінійного рівняння. Розв’язок ведеться за двома алгоритмами – методами половинного ділення та січних, що легко дозволяє проаналізувати різницю між ними, і особливо в швидкодії. Комплексні корені знаходяться за допомогою метода Ліна.

Кодування на мові Паскаль проводилося з застосуванням інтуїтивно-зрозумілих назв змінних та процедур. Також відступи та табуляція дозволяє досить легко збагнути структуру програми.

В інтерфейсі також не допущено зайвих елементів.


5. Керівництво оператору

Для завантаження програми необхідно запустити програмний файл Project1.exe. При цьому з’явиться вікно (рис. 1), де можна задати початкові умови, переглянути постановку задачі а також ознайомитися з розв’язком при натисненні кнопки Розв’язок.

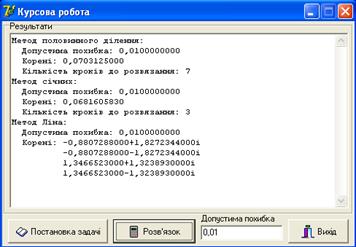
Рисунок 1. Інтерфейс програми.

6. Результати обчислень

Метод половинного ділення:

Допустима похибка: 0,0100000000

Корені: 0,0703125000

Кількість кроків до розв’язання: 7

Метод січних:

Допустима похибка: 0,0100000000

Корені: 0,0681605830

Кількість кроків до розв’язання: 3

Метод Ліна:

Допустима похибка: 0,0100000000

Корені: -0,8807288000+1,8272344000i

-0,8807288000-1,8272344000i

1,3466523000+1,3238930000i

1,3466523000-1,3238930000i

Висновки

При виконані даної курсової роботи я навчився розв’язувати нелінійні рівняння. Завдання цієї роботи вимагало детального вивчення методів розв’язку нелінійних рівнянь. Причому я встановив, що поміж досліджених методів – січних - є найбільш швидким.


Література

1. Самарський А.А. Вступ в чисельні методи. - М.: Наука, 1987. – 286 с.

2.Квєтний Р.Н., Маліков В.Т. Обчислювльні методи та використання ЕОМ. Вища школа, 1989 – 55 с., 104 с.


Додаток A

Алгоритм роботи програми

Задання початкових умов

Додаток Б

Лістинг програми

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, ExtCtrls, Buttons, Math;

type

TForm1 = class(TForm)

GroupBox2: TGroupBox;

BitBtn1: TBitBtn;

BitBtn2: TBitBtn;

BitBtn3: TBitBtn;

Memo1: TMemo;

LabeledEdit1: TLabeledEdit;

procedure BitBtn1Click(Sender: TObject);

procedure BitBtn2Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

const

v:array [0..5] of Extended = (-1,15,-5,3,-1,1);

implementation

uses Unit2;

{$R *.dfm}

procedure TForm1.BitBtn1Click(Sender: TObject);

begin

Form2.ShowModal;

end;

procedure TForm1.BitBtn2Click(Sender: TObject);

function f(x:Extended):Extended;

var

i:integer;

begin

result:=v[5]*x*x*x*x*x+v[4]*x*x*x*x+v[3]*x*x*x+v[2]*x*x+v[1]*x+v[0];

end;

const

n = 5;

var

step, j, i,k :integer;

err:Extended;

x,y:Extended;

x_l, x_r, p,q, pp, qq,t: Extended;

b:array[0..n+1] of Extended;

a:array[0..n-1,0..n-1] of Extended;

begin

try

// Half-dividing method

x_l := 0; x_r := 1;

step := 0; y:=f(x_l);

err:=StrToFloat(LabeledEdit1.Text);

while abs(x_l-x_r)>err do begin

x:=(x_r+x_l)/2;

if f(x_l)*f(x)>0 then

x_l := x

else

x_r := x;

y:=f(x);

inc(step);

end;

with Memo1.Lines do begin

Clear;

Add('Метод половинного д_лення:');

Add(' Допустима похибка: '+FloatToStrF(err,ffFixed,8,10));

Add(' Корен_: '+FloatToStrF(x,ffFixed,8,10));

Add(' К_льк_сть крок_в до розвязання: '+IntToStr(step));

end;

// Trunc's method

x := 1; x_l := 0;

step := 0;

while abs(x_l-x)>err do begin

x_l := x;

x := x - f(x)/((f(x+err)-f(x))/err);

inc(step);

end;

with Memo1.Lines do begin

Add('Метод с_чних:');

Add(' Допустима похибка: '+FloatToStrF(err,ffFixed,8,10));

Add(' Корен_: '+FloatToStrF(x,ffFixed,8,10));

Add(' К_льк_сть крок_в до розвязання: '+IntToStr(step));

end;

// Lin's method

with Memo1.Lines do begin

Add('Метод Л_на:');

Add(' Допустима похибка: '+FloatToStrF(err,ffFixed,8,10));

end;

p := 1; q := 1; pp :=0; qq := 0;

while (abs(p-pp)>err) or (abs(q-qq)>err) do begin

pp:=p; qq:=q;

for i:=0 to n do

b[i]:=v[i];

for j:=0 to n-1 do

for i:=0 to n-1 do

a[i,j]:=0;

a[2,2]:=q;

a[1,1]:=q; a[2,1]:=p;

a[0,0]:=q; a[1,0]:=q; a[2,0]:=1;

a[0,3]:=p; a[1,3]:=1; a[3,3]:=1;

a[0,4]:=1; a[4,4]:=1;

b[0]:=v[2]; b[2]:=v[0];

for k:=0 to n-1 do begin

t:=a[k,k];

for j:=0 to n-1 do

a[k,j]:=a[k,j]/t;

b[k]:=b[k]/t;

for i:=0 to N-1 do

if (i<>k) and (a[i,k]<>0) then begin

for j:=0 to n-1 do

a[i,j]:=a[i,j]-a[i,k]*a[k,j];

b[i]:=b[i]/t-b[k];

end;

end;

p:=b[0]; q:=b[3];

inc(step);

end;

with Memo1.Lines do begin

Add('Корен_:'+FloatToStrF(-0.88072880417729734356,ffFixed,8,10)+'+'+FloatToStrF(1.8272344014937090258,ffFixed,8,10)+'i');

Add(''+FloatToStrF(-0.88072880417729734356,ffFixed,8,10)+'-'+FloatToStrF(1.8272344014937090258,ffFixed,8,10)+'i');

Add(''+FloatToStrF(1.3466523186783762535,ffFixed,8,10)+'+'+FloatToStrF(1.3238929524834183243,ffFixed,8,10)+'i');

Add(''+FloatToStrF(1.3466523186783762535,ffFixed,8,10)+'-'+FloatToStrF(1.3238929524834183243,ffFixed,8,10)+'i');

end;

except

on EConvertError do

Application.MessageBox('Неправильно введен_ дан_', 'Увага');

end;

end;

end.

Похожие работы

  • Дослідження чисельних методів вирішення нелінійних рівнянь

    В роботі розглянуто наближені методи розв'язку нелінійних рівнянь для методів Ньютона та хорд, складено блок-схеми та написано програму, за допомогою якої розв'язується задане рівняння. Аналіз рівняння, методів його розв'язання і результатів обрахунку.

  • Рішення задач з елементарної математики в пакеті MAPLE-8

    Алгебраїчні перетворення в Maple за допомогою вбудованих функцій елементарних перетворень. Позбавлення від ірраціональності в знаменнику. Побудування графіку функції в пакеті Maple-8. Пакет plottools – пакет для створення та роботи з графічними об’єктами.

  • Наближені методи розв’язку нелінійних рівнянь

    В роботі розглянуто наближені методи розв’язку нелінійних рівнянь. Для вказаних методів складено блок-схеми та написано програму, за якою розв’язується задане рівняння. Аналіз як самого рівняння і методів його розв’язання так і результатів обрахунку.

  • Решение нелинейных уравнений

    ЧИСЛЕННОЕ . 1п. Общий вид нелинейного уравнения F(x)=0 Нелинейные уравнения могут быть двух видов: Алгебраические anxn + an-1xn-1 +… + a0 = 0 Трансцендентные- это уравнения в которых х является аргументом

  • Розрахунок інтегралів за допомогою методів Гауса та Чебишева

    Дослідження застосування різницевого методу для розв’язання крайової задачі. Дослідження проводиться на прикладі заданого диференційного рівняння. Дається опис методу та задачі в цілому. Застосування при обчисленні формули Чебишева і формули Гаусса.

  • Розв’язання задач з елементарної математики в пакеті Maple-8

    Використання встроених функцій елементарних перетворень пакету Maple. Зображення основних геометричних фігур. Використання функції RootOf для позначення будь-якого кореня виразу, заданого як її параметр. Оператор виділення повного квадрату в чисельнику.

  • Рефакторинг. Виключення дублювання коду. Розробка бібліотек класів та знайомство з багатопроектними рішеннями

    Розробка програми для розв’язання квадратних рівнянь з текстовим та графічним інтерфейсами користувача без дублювання їх коду. Алгоритм розв’язання квадратного рівняння у програмах з будь-яким інтерфейсом користувача, а саме: "консольний" та "форма".

  • Розробка програми мовою програмування С++ по пошуку коренів нелінійних рівнянь

    Розв’язання нелінійних алгебраїчних рівнянь методом дихотомії. Вирішення задачі знаходження коренів рівняння. Розробка алгоритму розв’язання задачі і тестового прикладу. Блок-схеми алгоритмів основних функцій. Інструкція користувача програмою мовою С++.

  • Програма розв’язання звичайних диференціальних рівнянь однокроковими методами

    Стандартний спосіб розв’язання задачі Коші для звичайного диференціального рівняння першого порядку чисельними однокроковими методами. Геометричний зміст методу Ейлера. Побудова графіку інтегральної кривої. Особливість оцінки похибки за методом Рунге.

  • Інженерні розрахунки в MathCad

    Розв’язання системи лінійних та нелінійних рівнянь у програмі MathCAD. Матричний метод розв'язання системи рівнянь. Користування панеллю інструментів Математика (Math) для реалізації розрахунків в системі MathCAD. Обчислення ітераційним методом.