Название: Векторы

Вид работы: доклад

Рубрика: Математика

Размер файла: 19.84 Kb

Скачать файл: referat.me-214548.docx

Краткое описание работы: Упорядоченную совокупность ( x1, x2, ... , xn ) n вещественных чисел называют n-мерным вектором.

Векторы

Упорядоченную совокупность ( x₁ , x₂ , ... , x_n ) n вещественных чисел называют n-мерным вектором, а числа x_i ( i = ) - компонентами, или координатами, вектора.

Если, например, некоторый автомобильный завод должен выпустить в смену 50 легковых автомобилей, 100 грузовых, 10 автобусов, 50 комплектов запчастей для легковых автомобилей и 150 комплектов для грузовых автомобилей и автобусов, то производственную программу этого завода можно записать в виде вектора (50, 100, 10, 50, 150), имеющего пять компонент. Векторы обозначают жирными строчными буквами или буквами с чертой или стрелкой наверху. Два вектора называются равными, если они имеют одинаковое число компонент и их соответствующие компоненты равны.

Компоненты вектора нельзя менять местами, например, (3, 2, 5, 0, 1) ≠ (2, 3, 5, 0, 1).

Произведением вектора x = (x₁ , x₂ , ... ,x_n ) на действительное число λ называется вектор x = ( λx₁ , λx₂ , ... , λx_n ).

Суммой векторов x = (x₁ , x₂ , ... ,x_n ) и y = (y₁ , y₂ , ... ,y_n ) называется вектор
x + y = (x₁ + y₁ , x₂ + y₂ , ... , x_n + y_n ).

N-мерное векторное пространство Rⁿ определяется как множество всех n-мерных векторов, для которых определены операции умножения на действительные числа и сложение.

Экономическая иллюстрация n-мерного векторного пространства: пространство благ (товаров). Под товаром мы будем понимать некоторое благо или услугу, поступившие в продажу в определенное время в определенном месте. Предположим, что существует конечное число наличных товаров n; количества каждого из них, приобретенные потребителем, характеризуются набором товаров

x = (x₁ , x₂ , ..., x_n ),

где через x_i обозначается количество i-го блага, приобретенного потребителем. Будем считать, что все товары обладают свойством произвольной делимости, так что может быть куплено любое неотрицательное количество каждого из них. Тогда все возможные наборы товаров являются векторами пространства товаров
C = { x = (x₁ , x₂ , ... , x_n )| x_i ≥ 0, i = }.

Система e₁ , e₂ , ... , e_m n-мерных векторов называется линейно зависимой, если найдутся такие числа λ₁ , λ₂ , ... , λ_m , из которых хотя бы одно отлично от нуля, что выполняется равенство λ₁ e₁ + λ₂ e₂ + ... + λ_m e_m = 0;

в противном случае данная система векторов называется линейно независимой, то есть указанное равенство возможно лишь в случае, когда все λ₁ = λ₂ = ... = λ_m = 0. Геометрический смысл линейной зависимости векторов в R³ , интерпретируемых как направленные отрезки, поясняют следующие теоремы.

Теорема 1. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.

Теорема 2. Для того, чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны.

Теорема 3. Для того, чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны.

Тройка некомпланарных векторов a, b, c называется правой, если наблюдателю из их общего начала обход концов векторов a, b, c в указанном порядке кажется совершающимся по часовой стрелке. B противном случае a, b, c - левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными.

Тройка e₁ , e₂ , e₃ некомпланарных векторов в R³ называется базисом, а сами векторы e₁ , e₂ , e₃ - базисными. Любой вектор a может быть единственным образом разложен по базисным векторам, то есть представлен в виде

а = x₁ e₁ + x₂ e₂ + x₃ e₃ , (1.1)

числа x₁ , x₂ , x₃ в разложении (1.1) называются координатами вектора a в базисе e₁ , e₂ , e₃ и обозначаются a(x₁ , x₂ , x₃ ). Если векторы e₁ , e₂ , e₃ попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты x₁ , x₂ , x₃ - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать i, j, k.

Будем предполагать, что в пространстве R³ выбрана правая система декартовых прямоугольных координат {0, i, j, k}.

Векторным произведением вектора а на вектор b называется вектор c, который определяется следующими тремя условиями:

1. Длина вектора c численно равна площади параллелограмма, построенного на векторах a и b, т. е. |c| = |a||b| sin (a^b).

2. Вектор c перпендикулярен к каждому из векторов a и b.

3. Векторы a, b и c, взятые в указанном порядке, образуют правую тройку.

Для векторного произведения c вводится обозначение c = [ab] или c = a x b.

Если векторы a и b коллинеарны, то sin(a^b) = 0 и [ab] = 0, в частности, [aa] = 0. Векторные произведения ортов: [ij] = k, [jk] = i, [ki] = j.

Если векторы a и b заданы в базисе i, j, k координатами a(a₁ , a₂ , a₃ ), b(b₁ , b₂ , b₃ ), то

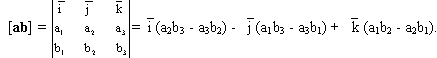
Если векторное произведение двух векторов а и b скалярно умножается на третий вектор c, то такое произведение трех векторов называется смешанным произведением и обозначается символом a b c.

Если векторы a, b и c в базисе i, j, k заданы своими координатами a(a₁ , a₂ , a₃ ),
b(b₁ , b₂ , b₃ ), c(c₁ , c₂ , c₃ ), то

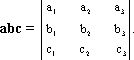
Смешанное произведение имеет простое геометрическое толкование - это скаляр, по абсолютной величине равный объему параллелепипеда, построенного на трех данных векторах.

Если векторы образуют правую тройку, то их смешанное произведение есть число положительное, равное указанному объему; если же тройка

a, b, c - левая, то abc < 0 и V = - abc, следовательно V = |abc| .

Координаты векторов, встречающиеся в задачах первой главы, предполагаются заданными относительно правого ортонормированного базиса. Единичный вектор, сонаправленный вектору а, обозначается символом а⁰ . Символом r=ОМ обозначается радиус-вектор точки М, символами а, АВ или |а| , |АВ| обозначаются модули векторов а и АВ.