Название: Теория вероятности

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 35.04 Kb

Скачать файл: referat.me-217766.docx

Краткое описание работы: Дискретные случайные величины и их распределения. Формула полной вероятности и формула Байеса. Общие свойства математического ожидания. Дисперсия случайной величины. Функция распределения случайной величины. Классическое определение вероятностей.

Теория вероятности

Вариант 10

(для студентов, номера личных дел которых оканчиваются цифрой 0)

Контрольная работа №3

1. На первом станке обработано 20 деталей, из них семь с дефектами, на втором - 30, из них четыре с дефектами, на третьем - 50 деталей, из них 10 с дефектами. Все детали сложены вместе. Наудачу взятая деталь оказалась без дефектов.

Какова вероятность того, что она обработана на третьем станке?

Для решения этой задачи воспользуемся формулой Байеса:

Пусть Н₁ , Н₂ , … Н_n – полная группа попарно несовместных событий гипотезы, А – случайное событие, тогда:

Введем гипотезы: Н₁ – деталь обработана на первом станке, Н₂ – деталь обработана на втором станке, Н₃ – деталь обработана на третьем станке.

Введем событие А – купленная деталь оказалась без дефектов.

Тогда, по условию задачи:

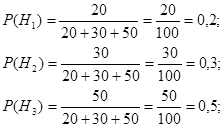
Так как на первом станке было изготовлено 20-7 = 13 деталей без дефектов, то

На втором станке было изготовлено 30-4 = 26 деталей без дефектов, то

А на третьем станке было изготовлено 50-10 = 40 деталей без дефектов, то

По формуле полной вероятности получаем:

По формуле Байеса:

Ответ:

2. Сколько семян следует взять, чтобы с вероятностью не менее чем 0,9545 быть уверенным, что частость взошедших семян будет отличаться от вероятности р - 0,9 не более чем на 2% (по абсолютной величине)?

Решение

По условию, р=0,9, тогда q=0,1. Необходимо найти n. Необходимо, чтобы условие

выполнялось с вероятностью, не меньшей, чем 0,9545. Раскроем модуль и найдем границы для m:

По теореме Муавра-Лапласа:

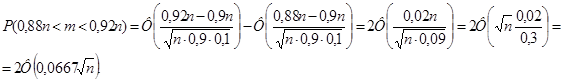
По условию, ≥0,9545.

По математико-статистическим таблицам находим приближенное значение функции Лапласса:

Ф(Х) = 0,9545, где Х=.

Имеем: Ф(Х) = 2,0 , отсюда

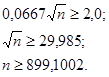
Итак, следует взять не менее 900 семян.

3. Завод «Пино» (г. Новороссийск) отправил в Москву 2000 бутылок вина « Каберне». Вероятность того, что в пути может разбиться бутылка, равна 0,002.

Какова вероятность того, что в пути будет разбито не более пяти бутылок?

Если проводится n независимых испытаний, в каждом из которых событие А может наступить с одной и той же вероятностью, тогда вероятность Р_n (m) того, что событие наступило m раз в этой серии испытаний можно найти:

Р(А) = ,

так как число n=2000 велико, а вероятность р=0,002 мала, то найдем:

то воспользуемся формулой Пуассона:

Искомая вероятность приближенно равна:

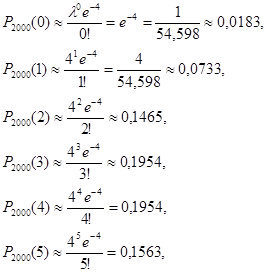
P = P₂₀₀₀ (0)+ P₂₀₀₀ (1)+ P₂₀₀₀ (2)+ P₂₀₀₀ (3)+ P₂₀₀₀ (4)+ P₂₀₀₀ (5)≈0,0183+0,0733+0,1465+0,1954+0,1954+0,1563 = 0,7852

Ответ: Р≈0,7852

4. Одна из случайных величин (X) задана законом распределения:

X	0	1	3
p	0,2	0,3	0,5

а другая (У) имеет биномиальное распределение с параметрами п=2,р=0,4.

Составить закон распределения их разности. Найти математическое ожидание и дисперсию этой случайной величины.

Найдем закон распределения для величины (Y):

y	0	1	2
p	p0 =0,36	p1 =0,48	p2 =0,16

Z₁₁ = X₁ - Y₁ = 0-0 = 0; p(Z₁₁ ) = 0,2·0,36=0,072;

Z₁₂ = X₁ - Y₂ = 0-1 = -1; p(Z₁₂ ) = 0,2·0,48=0,096;

Z₁₃ = X₁ - Y₃ = 0-2 = -2; p(Z₁₃ ) = 0,2·0,16=0,032;

Z₂₁ = X₂ - Y₁ = 1-0 = 1; p(Z₁₁ ) = 0,3·0,36=0,108;

Z₂₂ = X₂ - Y₂ = 1-1 = 0; p(Z₁₁ ) = 0,3·0,48=0,144;

Z₂₃ = X₂ - Y₃ = 1-2 = -1; p(Z₁₁ ) = 0,3·0,16=0,048;

Z₃₁ = X₃ - Y₁ = 3-0 = 3; p(Z₁₁ ) = 0,5·0,36=0,018;

Z₃₂ = X₃ - Y₂ = 3-1 = 2; p(Z₁₁ ) = 0,5·0,48=0,024;

Z₃₃ = X₃ - Y₃ = 3-2 = 1; p(Z₁₁ ) = 0,5·0,16=0,08.

Итак, закон распределения разности имеет вид:

Z	-2	-1	0	1	2	3
P	0,032	0,096+0,048=0,144	0,072+0,144=0,216	0,108+0,08=0,188	0,24	0,18

Мат. ожидание:

М(Z) = -2·0,032-1·0,144+0·0,216+1·0,188+2·0,24+3·0,18= -0,02+0,48+0,54 = 1

Проверка:

М(Х) = 0,3+1,5 = 1,8

М(Y) = np = 0,8

M(X-Y) = M(X) – M(Y) = 1,8-0,8 = 1.

Дисперсия:

D(Z) = M(Z² )-[M(Z)]²

M(Z² )=0,128+0,144+0+0,188+0,96+1,62 = 3,04

D(Z) = 3,04-1 = 2,04.

5. Полагая, что длина изготавливаемой детали есть нормально распределенная случайная величина с математическим ожиданием М{Х) = 10 и средним квадратическим отклонением δ = 2, найти вероятность того, что длина наугад взятой детали заключена в интервале (5; 6).

В каких границах (симметричных относительно М(Х)) будет заключена длина наугад взятой детали с вероятностью 0,95?

1.
2

Используя таблицу значений нормированной функции Лапласса, имеем:

Список использованной литературы

1. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. — 2-е изд., перераб. и доп.— М.: ЮНИТИ-ДАНА, 2004. - 573 с.