Название: Краткие сведения и задачи по курсу векторной и линейной алгебры
Вид работы: контрольная работа
Рубрика: Математика
Размер файла: 103.58 Kb
Скачать файл: referat.me-214618.docx
Краткое описание работы: Определение типа кривой по виду уравнения, уравнение с угловым коэффициентом, в отрезках и общее уравнение. Определение медианы, уравнения средней линии в треугольнике. Вопросы по линейной алгебре. Решение системы уравнения при помощи обратной матрицы.
Краткие сведения и задачи по курсу векторной и линейной алгебры
Контрольная работа
Краткие сведенияи задачи по курсу векторной и линейной алгебры
Векторная алгебра
Вариант №21
1. Найти скалярное произведение ![]() .
.
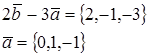
![]()
2. При каком значении α векторы ![]() и
и ![]() ортогональны?
ортогональны?
![]() ;
;![]() ;
;![]() ;
;
![]() ;
;![]() ;
;![]() ;
;
Два вектора ортогональны, когда их скалярное произведение равно нулю.
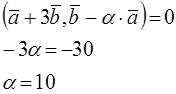
3. Для прямой М1 М2 написать уравнение с угловым коэффициентом, в отрезках и общее уравнение. Начертить график прямой. М1 (0,-3) М2 (2,1).
Общий вид уравнения прямой с угловым коэффициентом записывается в виде:
y-y1 =k(x-x1 ),
значит для прямой М1 М2
у+3=kx
Общий вид уравнения прямой, проходящей через две точки записывается в виде:
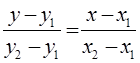 ,
,
значит для прямой М1 М2
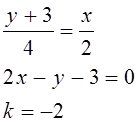
Общий вид уравнения прямой в отрезках записывается в виде:
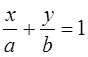 ,
,
Здесь
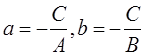
Уравнения прямой в отрезках для прямой М1 М2
![]() ;
;![]()
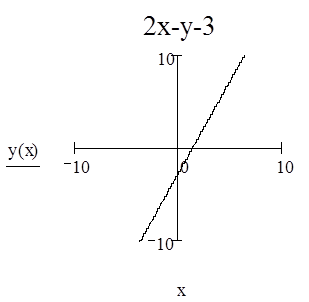
4. В треугольнике М0 М1 М2 найти уравнение медианы, высоты, проведенных их вершины М0 , а также уравнение средней линии EF, параллельной основанию М1 М2 .(М0 (-1,-2); М1 (0,-3); М2 (2,1)).
Найдём координаты точки М3 , координаты середины стороны М1 М2 :
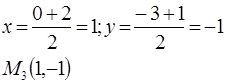
уравнения прямой, проходящей через две точки записывается в виде:
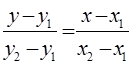 ,
,
уравнение для высоты М0 М3 :
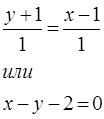
Найдём уравнение прямой М1 М2 :
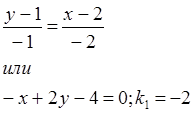
Из условия перпендикулярности (k2 =-1/k1 ) следует, что k2 =1/2.
Уравнения прямой с угловым коэффициентом записывается в виде:
y-y1 =k(x-x1 ),
тогда уравнение для высоты примет вид:
y+1= (x+2)/2
или
x+2y=0.
Расстояние от точки М(x0 ,y0 ) до прямой Ax+By+c=0 находится по формуле:
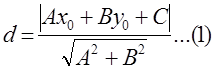
Чтобы найти длину высоту, найдём расстояние от точки М0 (-3,-5) до прямойМ1 М2 , уравнение которой имеет вид -x+2y-4=0. Подставим данные в формулу(1):
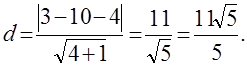
Найдём координаты точек Е иF.
Для точки Е: x=-1/2; y=-5/2; E(-1/2;-5/2).
Для точки F: x=1/2; y=-1/2; F(1/2;-1/2).
Уравнение прямой EF:
y+5/2=-2x-1 или 2x+y+3,5=0.
5. По каноническому уравнению кривой второго порядка определить тип кривой, начертить её график. Найти координаты фокусов, вершин и центра (для центральной кривой).
![]()
![]()
![]()
![]()
![]() (1)
(1)
Воспользуемся параллельным переносом (O’(-3,-1))
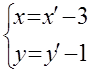 (2)
(2)
Подставим (2) в (1), получим
![]()
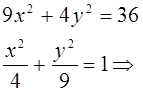
кривая второго порядка является эллипсом.
F1 (c;0); F2 (-c;0).
![]()
т.к.![]()
![]()
Координаты центра: O’(-3,-1).
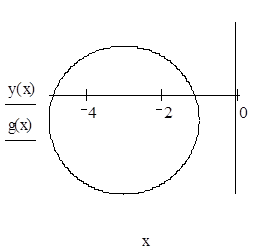
6. Преобразовать к полярным координатам уравнения линии.![]()
![]()
![]()
![]()
![]()
1)![]()
2) ![]()
Первое уравнение представляет собой (при любых значениях φ) полюс О. Второе – дает все точки линии, в том числе полюс. Поэтому первое уравнение можно отбросить. Следовательно, получаем:
![]()
Линейная алгебра
Матрицы
Ответы на вопросы
1. Дайте определение обратной матрицы. Какие вы знаете способы вычисления обратной матрицы?
Матрица В называется обратной для матрицы А, если выполняется условие АВ=ВА=Е, где Е – единичная матрица. Способы вычисления обратной матрицы: 1) использование алгебраических дополнений; 2) привести исходную матрицу к ступенчатому виду методом Гаусса, после чего необходимо преобразовать её в единичную ![]() .
.
2. Как записывается система уравнений в матрично-векторной форме? Как найти решение системы уравнений при помощи обратной матрицы?
Система уравнений в матрично-векторной форме записывается в виде: ![]() .
.
Решение системы уравнения при помощи обратной матрицы:
![]()
3. Сформулируйте, в чем состоит процедура Гаусса и для решения каких линейных задач применяется?
Процедура Гаусса используется для решения систем линейных уравнений и состоит в следующем:
Выполняются элементарные преобразования, вследствие чего можно получить два исхода:
1. получается строчка, в которой до черты стоят нули, а после – ненулевое число, тогда решения нет;
2. система приводится к лестничному виду.
Если в системе лестничного вида число уравнений совпадает с числом неизвестных, то решение единственное.
Если число уравнений меньше чем число неизвестных, то решений бесконечное множество. В этом случае неизвестные разделяются на зависимые и свободные. Число зависимых неизвестных совпадает с числом уравнений.
Задача1.
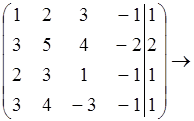
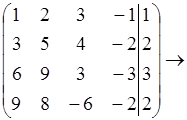
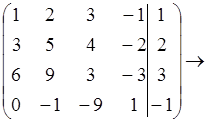
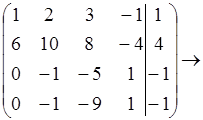
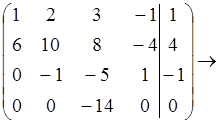
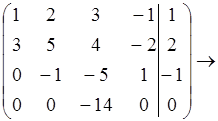
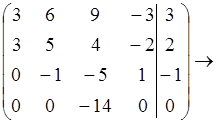
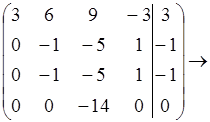
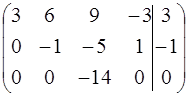
X4-свободная переменная
r = 3
система совместима.
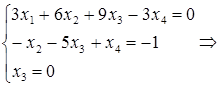
![]()
Задача2
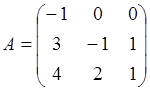
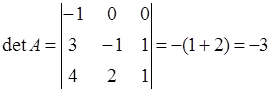
т.к. detA![]() 0, то матрица является невырожденной.
0, то матрица является невырожденной.
А11 =3;А12 = -1;А13 = -10;А21 =0;А22 =0;А23 = -1;А31 =0;А32 = -1;А33 = -1.
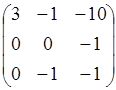 ;
;
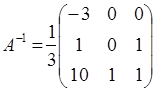 .
.
![]()
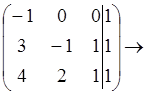
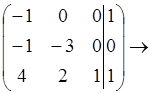
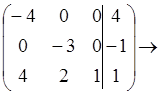
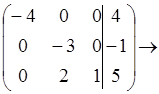
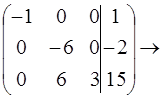
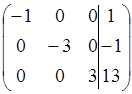 .
.
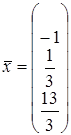 .
.
5. Найти скалярное произведение ![]() .
.
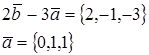
![]()
6. При каком значении α векторы ![]() и
и ![]() ортогональны?
ортогональны?
![]() ;
;![]() ;
;![]() ;
;
![]() ;
;![]() ;
;![]() ;
;
Два вектора ортогональны, когда их скалярное произведение равно нулю.
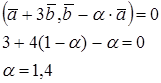
7. Для прямой М1 М2 написать уравнение с угловым коэффициентом, в отрезках и общее уравнение. Начертить график прямой. М1 (2,-2) М2 (1,0).
Общий вид уравнения прямой с угловым коэффициентом записывается в виде:
y-y1 =k(x-x1 ),
значит для прямой М1 М2
у+2=k(x-2)
Общий вид уравнения прямой, проходящей через две точки записывается в виде:
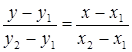 ,
,
значит для прямой М1 М2
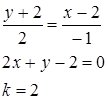
Общий вид уравнения прямой в отрезках записывается в виде:
![]() ,
,
здесь ![]()
Уравнения прямой в отрезках для прямой М1 М2
![]() ;
;![]()
y=-2x+2
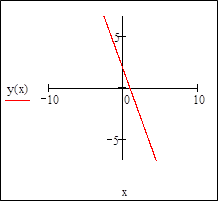
8. В треугольнике М0 М1 М2 найти уравнение медианы, высоты, проведенных их вершины М0 , а также уравнение средней линии EF, параллельной основанию М1 М2 .(М0 (-3,-5); М1 (2,-2); М2 (1,0)).
Найдём координаты точки М3 , координаты середины стороны М1 М2 :
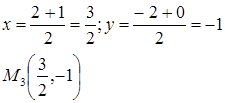
уравнения прямой, проходящей через две точки записывается в виде:
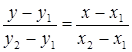 ,
,
уравнение для высоты М0 М3 :
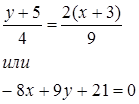
Найдём уравнение прямой М1 М2 :
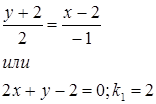
Из условия перпендикулярности (k2 =-1/k1 ) следует, что k2 =-1/2.
Уравнения прямой с угловым коэффициентом записывается в виде:
y-y1 =k(x-x1 ),
тогда уравнение для высоты примет вид:
y+5= -(x+3)/2
или
x+2y+13=0.
Расстояние от точки М(x0 ,y0 ) до прямой Ax+By+c=0 находится по формуле:
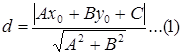
Чтобы найти длину высоту, найдём расстояние от точки М0 (-3,-5) до прямойМ1 М2 , уравнение которой имеет вид 2x+y-2=0. Подставим данные в формулу(1):
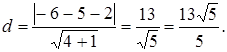
Найдём координаты точек Е иF.
Для точки Е: x=-1/2; y=-7/2; E(-1/2;-7/2).
Для точки F: x=-1; y=-5/2; F(-1;-5/2).
Уравнение прямой EF:
y+7/2=-2x-1 или 2x+y+4,5=0.
9. По каноническому уравнению кривой второго порядка определить тип кривой, начертить её график. Найти координаты фокусов, вершин и центра (для центральной кривой).
![]()
![]()
![]()
![]()
![]() (1)
(1)
Воспользуемся параллельным переносом (O’(-2,2))
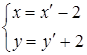 (2)
(2)
Подставим (2) в (1), получим
![]()
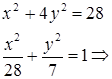
кривая второго порядка является эллипсом.
F1 (c;0); F2 (-c;0).
![]()
т.к.![]()
![]()
Координаты центра: O’(-2,2).
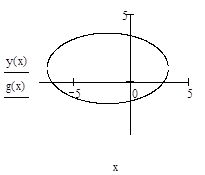
10. Преобразовать к полярным координатам уравнения линии.![]()
![]()
![]()
![]()
![]()
1) ![]()
2) ![]()
Первое уравнение представляет собой (при любых значениях φ) полюс О. Второе – дает все точки линии, в том числе полюс,. Поэтому первое уравнение можно отбросить. Следовательно получаем:
![]()
Ответы на вопросы
4. Дайте определение обратной матрицы. Какие вы знаете способы вычисления обратной матрицы?
Матрица В называется обратной для матрицы А, если выполняется условие АВ=ВА=Е, где Е – единичная матрица. Способы вычисления обратной матрицы: 1) использование алгебраических дополнений; 2) привести исходную матрицу к ступенчатому виду методом Гаусса, после чего необходимо преобразовать её в единичную ![]() .
.
5. Как записывается система уравнений в матрично-векторной форме? Как найти решение системы уравнений при помощи обратной матрицы?
Система уравнений в матрично-векторной форме записывается в виде:
![]() .
.
Решения системы уравнения при помощи обратной матрицы:
![]()
6. Сформулируйте, в чем состоит процедура Гаусса и для решения каких линейных задач применяется?
Процедура Гаусса используется для решения систем линейных уравнений и состоит в следующем:
Выполняются элементарные преобразования, вследствие чего можно получить два исхода:
3. получается строчка, в которой до черты стоят нули, а после – ненулевое число, тогда решения нет;
4. система приводится к лестничному виду.
Если в системе лестничного вида число уравнений совпадает с числом неизвестных, то решение единственное.
Если число уравнений меньше чем число неизвестных, то решений бесконечное множество. В этом случае неизвестные разделяются на зависимые и свободные. Число зависимых неизвестных совпадает с числом уравнений.
Задача1.
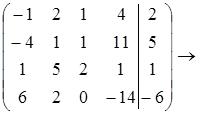
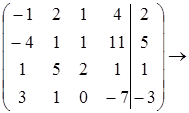
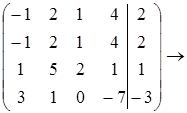
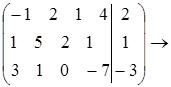
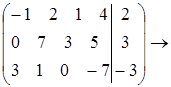
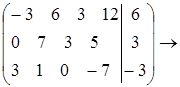
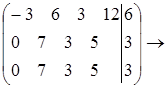
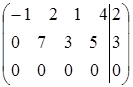 r=2; система совместима.
r=2; система совместима.
х 3,x4 – свободные переменные
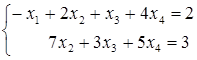
![]() ;
;![]() .
.
Задача2.
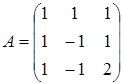
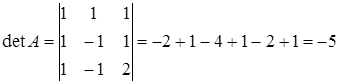
т.к. detA![]() 0, то матрица невырождена.
0, то матрица невырождена.
А11 =-1; А12 =-3; А13 =-1;А21 =-3;А22 =1;А23 =2;А31 =2;А32 =-1;А33 = -3.
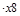
![]()
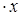
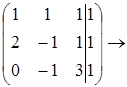
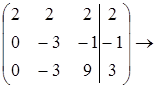
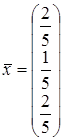 .
.
Похожие работы
-
Исследование кривых и поверхностей второго порядка
Кафедра высшей математики Курсовая работа по линейной алгебре и аналитической геометрии на тему: Исследование кривых и поверхностей второго порядка
-
Лекции по математике
Раздел 1. Элементы линейной алгебры. 1.1 Матрицы, определители. Вопросы: 1.1.1. Определение матриц, виды матриц; 1.1.2. Операции над матрицами; 1.1.3. Определители;
-
Решение линейной системы уравнений с тремя неизвестными
Решение системы линейных уравнений двумя способами: по формулам Крамера и методом Гаусса. Решение задачи на нахождение производных, пользуясь правилами и формулами дифференцирования. Исследование заданных функций методами дифференциального исчисления.
-
Алгебра матриц. Системы линейных уравнений
Выполнение действий над матрицами. Определение обратной матрицы. Решение матричных уравнений и системы уравнений матричным способом, используя алгебраические дополнения. Исследование и решение системы линейных уравнений методом Крамера и Гаусса.
-
Дифференциальные уравнения
Основные понятия и определения.
-
Площадь треугольника
Задача Дано: треугольник с вершинами в точках А [4; 0] B [3; 20] [5; 0]. Найти: a) Уравнение прямой b) Уравнение высоты , проведенной к стороне c) Уравнение прямой
-
Линейные функции
Общее уравнение прямой, переходящей через определенную точку. Условия перпендикулярности прямых. Условие перпендикулярности плоскостей. Свойства медианы треугольника. Нахождение направляющих векторов прямых. Условие параллельности прямой и плоскости.
-
Дифференциальные уравнения линейных систем автоматического регулирования
Определение динамических свойств объектов с помощью дифференциальных уравнений для сравнительно простых объектов. Выражение входной и выходной величины элемента в долях, введение безразмерных координат. График кривой разгона, коэффициент усиления.
-
Понятие и сущность науки высшая математика
Содержание Введение 2 1 Прямая на плоскости 4 1.1Определение прямой линии 4 1.2 Прямая на плоскости 4 1.2.1 Общее уравнение прямой 4 1.2.2 Уравнение прямой в отрезках 6
-
Задачи по Математике
ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ Задачи № 1-10. Решить систему линейных алгебраических уравнений тремя способами: 1) методом Крамера, 2) с помощью обратной матрицы, 3) методом Гаусса.