Referat.me
/ / Алгебра матриц. Системы линейных уравнений

Название: Алгебра матриц. Системы линейных уравнений

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 67.5 Kb

Скачать файл: referat.me-217546.docx

Краткое описание работы: Выполнение действий над матрицами. Определение обратной матрицы. Решение матричных уравнений и системы уравнений матричным способом, используя алгебраические дополнения. Исследование и решение системы линейных уравнений методом Крамера и Гаусса.

Алгебра матриц. Системы линейных уравнений

Вариант 6

Тема: Алгебра матриц

Задание: Выполнить действия над матрицами.

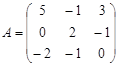
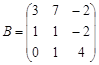
1) С=3A-(A+2B)B

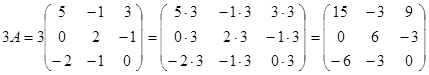
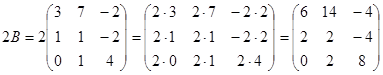
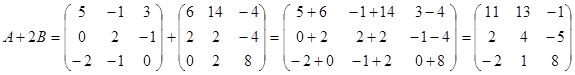
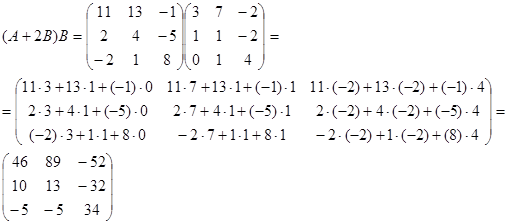
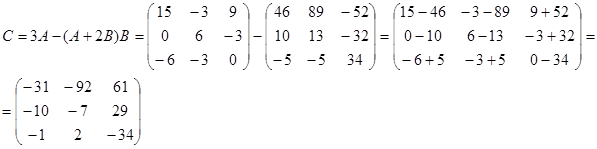
2) D=A2 +B2 +4E2

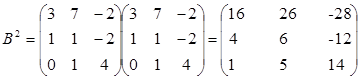
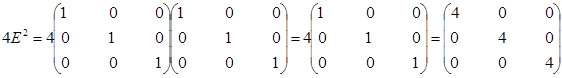
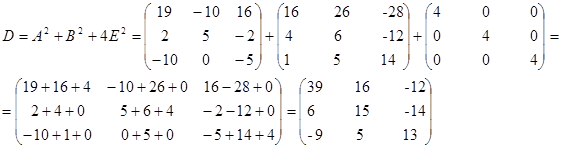
Тема: Обращение матриц

Обратить матрицу по определению:

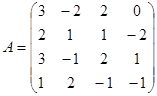
Определитель матрицы:

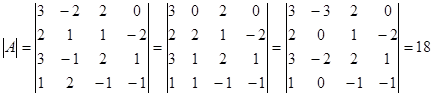
Далее находим матрицу алгебраических дополнений (союзную матрицу):

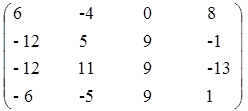
Обратную матрицу находим:

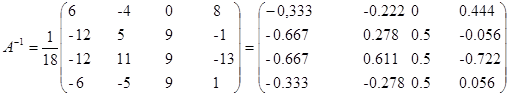
По определению обратной матрицы:

Действительно:

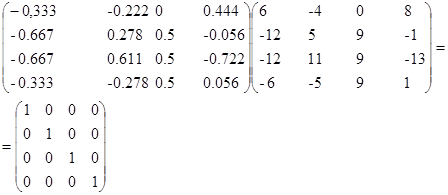
Тема: решение матричных уравнений

Задание 1: Решить матричное уравнение:

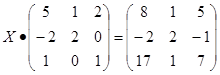
Решение.

Нахождение столбца Х сводится к умножению матрицы на обратную:

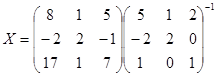
Матрица коэффициентов А:


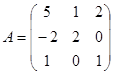
Найдем обратную матрицу A-1 :

Определитель матрицы A:

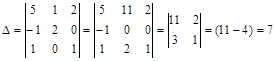
Алгебраические дополнения:

Транспонированная матрица алгебраических дополнений:

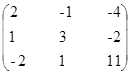
Запишем выражение для обратной матрицы:

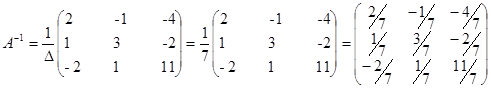
Итак, выполняем умножение матриц и находим матрицу X:


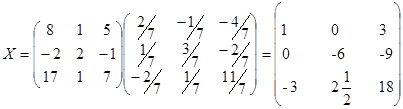
Ответ:

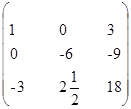
Задание 2: Решить систему уравнений матричным способом

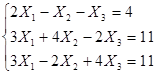
Решение

Матричная запись уравнения:

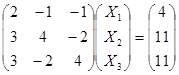
Матрица коэффициентов А:


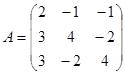
Найдем обратную матрицу A-1 :

Определитель матрицы A:

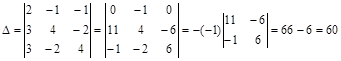
Алгебраические дополнения:

Транспонированная матрица алгебраических дополнений (союзная матрица):

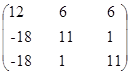
Запишем выражение для обратной матрицы:

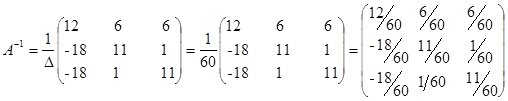
Вычислим столбец неизвестных:


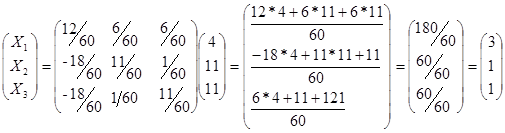
Тема: Решение систем линейных уравнений методом Крамера и Гаусса

Задание 1: Исследовать и решить систему по формулам Крамера:

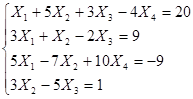
Найти решение системы уравнений по методу Крамера.

Согласно методу Крамера, если определитель матрицы системы ненулевой, то система из 4-х уравнении имеет одно решение, при этом значение корней:

,,,,

Где:

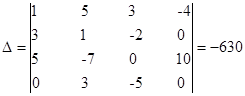- определитель матрицы коэффициентов – ненулевой.


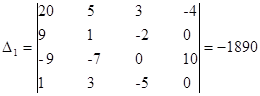- определитель матрицы полученной путем замены первого столбца матрицы коэффициентов на столбец свободных членов.

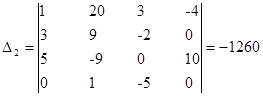- определитель матрицы полученной заменой второго столбца матрицы коэффициентов на столбец свободных членов.

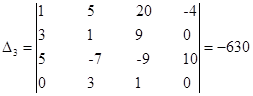- определитель матрицы полученной заменой третьего столбца матрицы коэффициентов на столбец свободных членов.

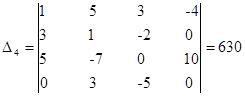- определитель матрицы полученной заменой четвертого столбца матрицы коэффициентов на столбец свободных членов.

Итак:


,

,

.

Задание 2: Решить эту систему по методу Гаусса.

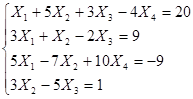
Метод Гаусса заключается в сведении системы к треугольному виду.

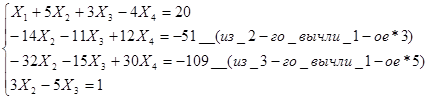
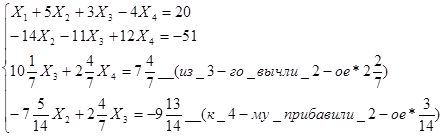
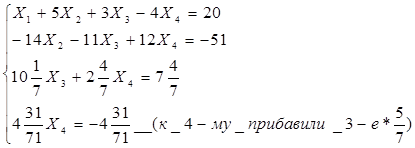
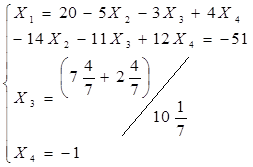
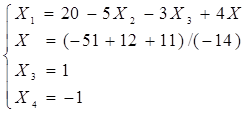
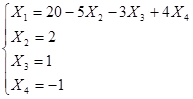
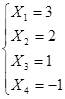
Видим, что решение системы по методу Гаусса совпадает с решением по методу Крамера.

Похожие работы

  • Системы линейных уравнений и неравенств

    Основные понятия теории систем уравнений. Метод Гаусса — метод последовательного исключения переменных. Формулы Крамера. Решение систем линейных уравнений методом обратной матрицы. Теорема Кронекер–Капелли. Совместность систем однородных уравнений.

  • Система уравнений по формулам Крамера

    Задание № 1 Решить систему уравнений: 1) по формулам Крамера 2) с помощью обратной матрицы 3) методом Гаусса Решение найдем определитель матрицы 1) методом Крамера

  • Элементы аналитической геометрии

    ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» ИНСТИТУТ ЭКОНОМИКИ И ВНЕШНЕЭКОНОМИЧЕСКИХ СВЯЗЕЙ

  • Определитель матрицы 2

    Оглавление Задача 2 3 Задача 3 5 Задача 4 7 Задача 1 Вычислить определитель 4-го порядка. Решение: Определитель 4-го порядка находится по формуле: aij – элемент матрицы;

  • Матрицы

    Общие определения, связанные с понятием матрицы. Действия над матрицами. Определители 2-го и 3-го порядков, порядка n, порядок их вычисления и характерные свойства. Обратные матрицы и их ранг. Понятие и этапы элементарного преобразования матрицы.

  • Метод Крамера

    Министерство рыбного хозяйства Владивостокский морской колледж ТЕМА: “ Системы 2-х , 3-х линейных уравнений. Правило Крамера. ” г. Владивосток

  • Матричная форма формулы Крамера

    С.К. Соболев Матричный способ решения СЛАУ, формулы Крамера, свойство присоединенной матрицы и основное свойство линейной зависимости. Рассмотрим

  • Основы высшей матиматики

    Вычисление определителя 4-го порядка, математическое решение системы методами матрицы, Крамера и Гаусса. Характеристика понятий невырожденной и обратной, транспонированной и присоединенной матрицы, нахождение алгебраических дополнений элементов таблицы.

  • Задачи по Математике

    ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ Задачи № 1-10. Решить систему линейных алгебраических уравнений тремя способами: 1) методом Крамера, 2) с помощью обратной матрицы, 3) методом Гаусса.

  • Системы линейных уравнений

    Критерий совместности. Метод Гаусса. Формулы Крамера. Матричный метод.