Название: Существование решения дифференциального уравнения и последовательные приближения
Вид работы: реферат
Рубрика: Математика
Размер файла: 93.8 Kb
Скачать файл: referat.me-214764.docx
Краткое описание работы: Теорема существования и единственности решения уравнения.
Существование решения дифференциального уравнения и последовательные приближения
Курсовая работа
Выполнил студент 2 курса 1222 группы Труфанов Александр Николаевич
Государственное образовательное учреждение высшего профессионального образования «Самарский государственный университет»
Механико-математический факультет
Кафедра дифференциальных уравнений и теории управления
Самара 2004
Теорема существования и единственности решения уравнения
Пусть дано уравнение
![]()
с начальным условием
![]()
Пусть в замкнутой области R![]() функции
функции ![]() и
и ![]() непрерывны). Тогда на некотором отрезке
непрерывны). Тогда на некотором отрезке ![]() существует единственное решение, удовлетворяющее начальному условию
существует единственное решение, удовлетворяющее начальному условию ![]() .
.
Последовательные приближения определяются формулами:
![]()
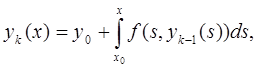 k = 1,2....
k = 1,2....
Задание №9
Перейти от уравнения
![]()
к системе нормального вида и при начальных условиях
![]() ,
, ![]() ,
, ![]()
построить два последовательных приближения к решению.
Произведем замену переменных
![]() ;
; ![]()
и перейдем к системе нормального вида:
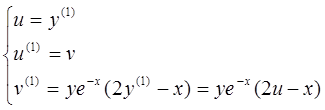
Построим последовательные приближения
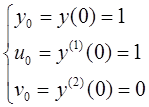
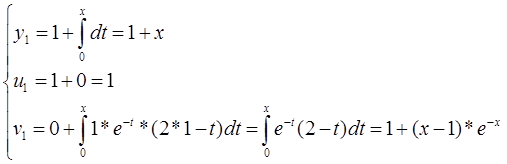
Задание №10
Построить три последовательных приближения ![]() к решению задачи
к решению задачи
![]() ,
, ![]()
Построим последовательные приближения
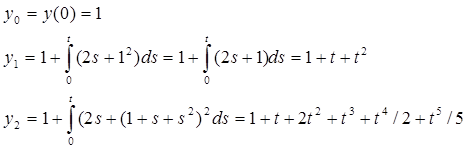
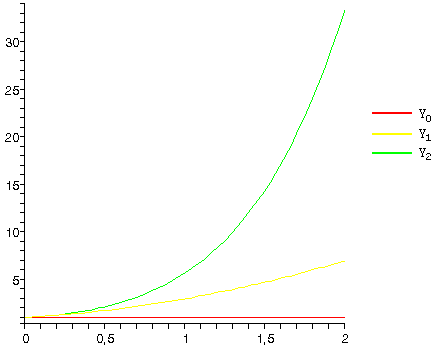
Задание №11
а) Задачу
![]() ,
, ![]()
свести к интегральному уравнению и построить последовательные приближения ![]()
б) Указать какой-либо отрезок, на котором сходятся последовательные приближения, и доказать их равномерную сходимость.
Сведем данное уравнение к интегральному :
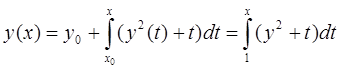
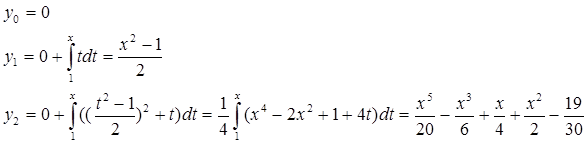
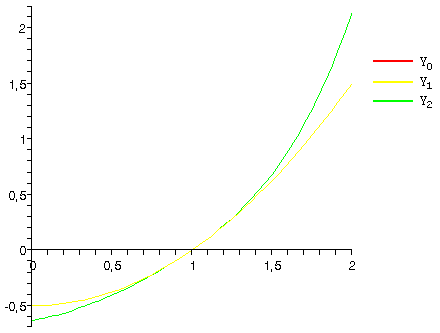
Докажем равномерную сходимость последовательных приближений
С помощью метода последовательных приближений мы можем построить последовательность
![]()
непрерывных функций, определенных на некотором отрезке ![]() , который содержит внутри себя точку
, который содержит внутри себя точку ![]() . Каждая функция последовательности определяется через предыдущую при помощи равенства
. Каждая функция последовательности определяется через предыдущую при помощи равенства
![]()
![]() i = 0, 1, 2 …
i = 0, 1, 2 …
Если график функции ![]() проходит в области Г, то функция
проходит в области Г, то функция ![]() определена этим равенством, но для того, чтобы могла быть определена следующая функция
определена этим равенством, но для того, чтобы могла быть определена следующая функция ![]() , нужно, чтобы и график функции
, нужно, чтобы и график функции ![]() проходил в области Г. Этого удается достичь, выбрав отрезок
проходил в области Г. Этого удается достичь, выбрав отрезок ![]() достаточно коротким. Далее, за счет уменьшения длины отрезка
достаточно коротким. Далее, за счет уменьшения длины отрезка ![]() , можно достичь того, чтобы для последовательности
, можно достичь того, чтобы для последовательности ![]() выполнялись неравенства:
выполнялись неравенства:
![]() , i = 1, 2, …,
, i = 1, 2, …,
где 0 < k < 1. Из этих неравенств вытекает следующее:
![]() , i = 1, 2, …,
, i = 1, 2, …,
Рассмотрим нашу функцию на достаточно малом отрезке, содержащим ![]() , например, на
, например, на ![]() . На этом промежутке все последовательные приближения являются непрерывными функциями. Очевидно, что т.к. каждое приближение представляет из себя функцию от бесконечно малого более высокого порядка, чем предыдущее приближение, то выполняются и описанные выше неравенства. Из этих неравенств следует:
. На этом промежутке все последовательные приближения являются непрерывными функциями. Очевидно, что т.к. каждое приближение представляет из себя функцию от бесконечно малого более высокого порядка, чем предыдущее приближение, то выполняются и описанные выше неравенства. Из этих неравенств следует:
![]()
что и является условием равномерной сходимости последовательных приближений.
С другой стороны, на нашем отрезке выполняется 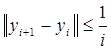 , что также совершенно очевидно. А так как последовательность
, что также совершенно очевидно. А так как последовательность ![]() сходится, то последовательность приближений является равномерно сходящийся на этом отрезке.
сходится, то последовательность приближений является равномерно сходящийся на этом отрезке.
Список литературы
Л.С. Понтрягин. «Обыкновенные дифференциальные уравнения», М.: Государственное издательство физико-математической литературы, 1961
А.Ф. Филиппов «Сборник задач по дифференциальным уравнениям», М.: Интеграл-Пресс, 1998
О.П. Филатов «Лекции по обыкновенным дифференциальным уравнениям»,Самара: Издательство «Самарский университет», 1999
А.Н. Тихонов, А.Б. Васильева «Дифференциальные уравнения», М.: Наука. Физматлит, 1998
Похожие работы
-
Решение нелинейных уравнений
Задание №1 Отделить корни уравнения графически и уточнить один из них: · методом половинного деления; · методом хорд; · методом касательных; · методом секущих;
-
Особое решение дифференциальных уравнений первого порядка
Введение Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
-
Контрольная работа
385. Вычислить несобственные интегралы или установить их расходимость. По определению несобственного интеграла имеем: Интеграл сходится. 301. Найти неопределенный интеграл.
-
Об одном аналоге задачи Бицадзе-Самарского для смешанно-составного уравнения
Бабаев Х. Об одном аналоге задачи Бицадзе-Самарского для смешанно-составного уравнения. РЕФЕРАТ В данной работе для смешанно-составного уравнения ставится и исследуется одна нелокальная краевая задача, которая является некоторым аналогом задачи Бицадзе-Самарского. Единственность решения изучаемой задачи доказывается принципом максимума, а существование решения доказывается сведением изучаемой задачи к эквивалентному ей интегральному уравнению.
-
Решение нелинейных уравнений методом простых итераций
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ВОСТОЧНО-СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ Реферат на тему: «Решение нелинейных уравнений
-
Доказательство великой теоремы Ферма
Доказательство теоремы Ферма методами теоремы арифметики, элементарной алгебры с использованием методов решения параметрических уравнений для четных и нечетных показателей степени. Теорема о разложении на простые множители целых составных чисел.
-
Интеграл дифференциального уравнения
Проверка непрерывности заданных функций. Интегрирование заданного уравнения и выполние преобразования с ним. Интегрирование однородного дифференциального уравнения. Решение линейного дифференциального уравнения. Общее решение неоднородного уравнения.
-
Анализ дифференциальных уравнений
Порядок и процедура поиска решения дифференциального уравнения. Теорема существования и единственности решения задачи Коши. Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка, с разделяющими переменными.
-
Решение систем нелинейных уравнений методом Ньютона
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ КАМСКАЯ ГОСУДАРСТВЕННАЯ ИНЖЕНЕРНО-ЭКОНОМИЧЕСКАЯ АКАДЕМИЯ
-
Краткое доказательство великой теоремы Ферма
Теорема Ферма, ее формулировка и доказательство в случаях, если показатель степени n - нечетное число и если n - четное число. Теорема о единственности факторизации. Дополнительные обоснования теоремы. Состав наибольшего составного числового множителя.