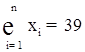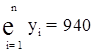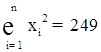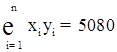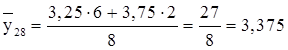Название: Теорія ймовірностей та математична статистика

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 411.3 Kb

Скачать файл: referat.me-217983.docx

Краткое описание работы: Міністерство освіти і науки України Донбаський державний технічний університет Кафедра Вищої Математики КОНТРОЛЬНА РОБОТА По дисципліні “Теорія ймовірностей та математична статистика”

Теорія ймовірностей та математична статистика

Міністерство освіти і науки України

Донбаський державний технічний університет

Кафедра Вищої Математики

КОНТРОЛЬНА РОБОТА

По дисципліні “Теорія ймовірностей та математична статистика”

Варіант №26

(завдання №14, 2, 4, 12, 11, 15, 2, 14, 3, 6)

Виконала : студентка групи

Перевірила: доцент кафедри вищ. мат.

Алчевськ 2009

РОЗДІЛ I “ТЕОРІЯ ЙМОВІРНОСТЕЙ”

ЗАВДАННЯ №1

14) В урні 2 білі і 3 чорні кульки. Двоє по черзі беруть навмання по одній кульці. Яка імовірність того, що з них перша біла, а друга чорна?

РОЗВ’ЯЗАННЯ

Для білої:

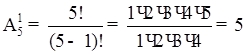
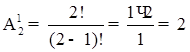
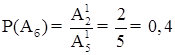
Для чорної:

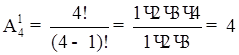
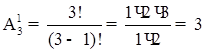
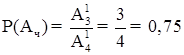
Загальна вірогідність:

або

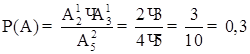
ЗАВДАННЯ №2

2) В першій урні 3 білих і 2 чорних кульки, а в другій 4 білих і 4 чорних кульки. З першої урни в другу навмання перекладають одну кульку, потім з другої урни взяли одну кульку. Яка імовірність, що вона біла?

РОЗВ’ЯЗАННЯ

Вірогідність того, що з першої урни переклали білу кульку:

Вірогідність того, що з другої урни узяли білу кульку:

ЗАВДАННЯ №3

4) 4.1 Обчислити ймовірність того, що деяка подія не відбудеться, якщо відомо, що при випробуваннях вона в середньому відбувається в випадках.

РОЗВ’ЯЗАННЯ

4.2 З 60 питань, що входять до екзаменаційних білетів, студент підготував 50. Яка ймовірність того, що взятий навмання студентом білет, який містить два питання, буде складатися з підготовлених ним питань?

РОЗВ’ЯЗАННЯ

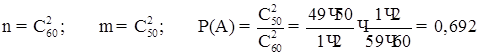
4.3 Яка ймовірність того, що серед вийнятих навмання 4 карт з повної колоди (52 карти), дві виявляться пікової масті?

РОЗВ’ЯЗАННЯ

ЗАВДАННЯ №4

12) Проведено незалежних випробувань, в кожному з яких може відбутися подія з імовірністю .

I) за локальною теоремою Муавра-Лапласа знайти імовірність того, що подія відбудеться рівно разів;

II) за інтегральною теоремою Муавра-Лапласа знайти імовірність того, що подія відбудеться від 700 разів до разів.

РОЗВ’ЯЗАННЯ

I)

1) Скористуємось формулою Муавра-Лапласа:

2) Знайдемо :

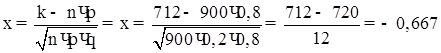
3) Знайдемо :

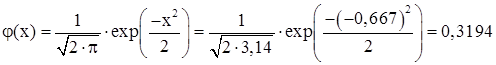
4) Шукана ймовірність:

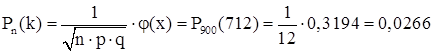
II)

За інтегральною теоремою Лапласа:

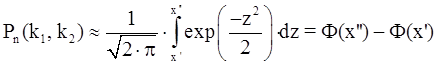
1) Знайдемо межі інтеграла і :

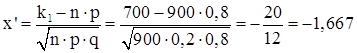
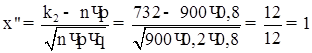
2) Знайдемо функції Лапласа і :

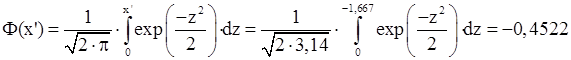
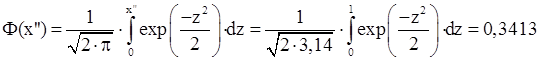
3) Шукана ймовірність:

ЗАВДАННЯ №5

11) Дискретна випадкова величина задана рядом розподілу. Знайти функцію розподілу і побудувати її графік. Знайти математичне сподівання і дисперсію випадкової величини.

Х	2	4	5
Р	0,2	0,6	0,2

РОЗВ’ЯЗАННЯ

1) Математичне сподівання знайдемо за формулою:

2) Складемо закон розподілу для :

Х	4	16	25
Р	0,2	0,6	0,2

3) Дисперсію знайдемо за формулою:

4) Середнє квадратичне відхилення знайдемо за формулою:

5) Знайдемо функцію розподілу:

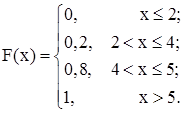
6) Графік цієї функції має вигляд:

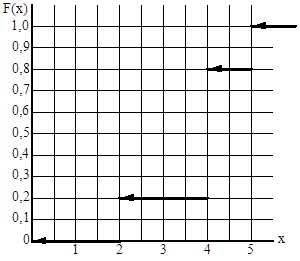
ЗАВДАННЯ №6

15) Випадкова величина задана функцією розподілу:

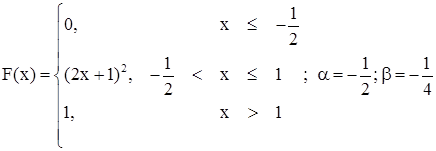
Знайти:

I) щільність розподілу ймовірності;

II) математичне сподівання;

III) дисперсію випадкової величини;

IV) імовірність попадання випадкової величини в інтервал ;

V) Накреслити графіки функцій і .

РОЗВ’ЯЗАННЯ

I) щільність розподілу ймовірностей:

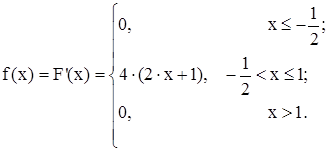
II) математичне сподівання:

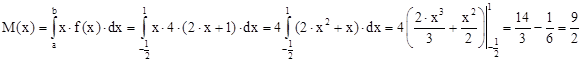
III) дисперсія:

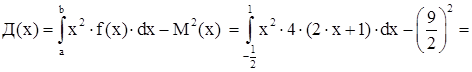
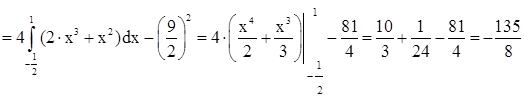
IV) імовірність того, що випадкова величина прийме значення з інтервалу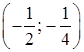

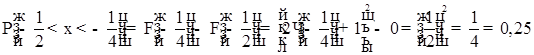
V) Графіки функцій і :

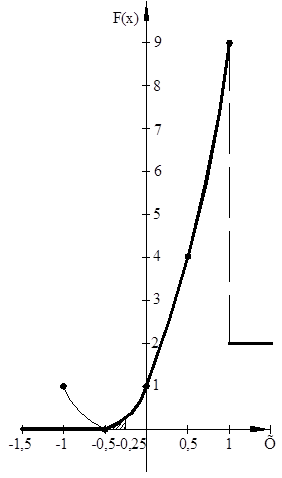
ЗАВДАННЯ №7

2) Відоме математичне сподівання і дисперсія випадкової величини .

Знайти:

I) імовірність попадання цієї величини в заданий інтервал ;

II) імовірність того, що абсолютна величина відхилення випадкової величини від свого математичного сподівання менша за число .

РОЗВ’ЯЗАННЯ

I) Імовірність влучення випадкової величини у інтервал :

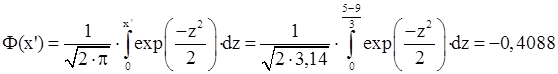
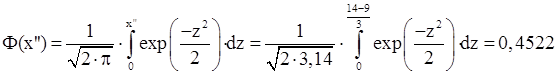
II) Імовірність того, що абсолютна величина відхилення випадкової величини від свого математичного сподівання буде менше 2, можна обчислити за формулою:

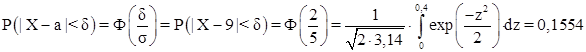
РОЗДІЛ II

14) РОЗРАХУНКОВА РОБОТА №1 “СТАТИСТИЧНИЙ РОЗПОДІЛ ВИБІРКИ”

23	26	31	35	38	43	48	39	36	27
43	39	37	34	31	27	21	33	32	44
24	28	30	35	33	39	40	41	46	36
42	39	35	32	27	29	33	35	38	41
25	30	30	31	32	34	36	37	38	40

перший інтервал 21-25

Представити кожну вибірку у вигляді таблиці частот згрупованої вибірки, побудувати гістограму і полігон частот, записати емпіричну функцію розподілу і побудувати їх графік.

РОЗВ’ЯЗАННЯ

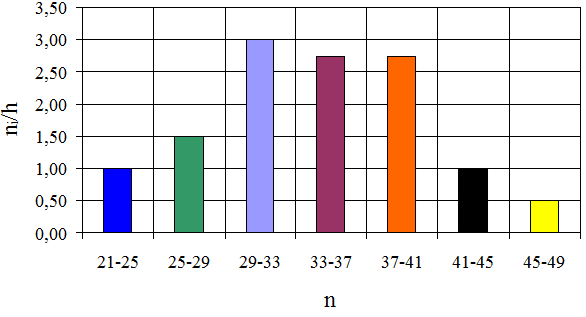
1) Складемо таблицю частот згрупованої вибірки:

Межі інтервалу xi xi+1	Середина інтервалу xi 0	Частота ni	Накопичувальна частота Σni	Відносна частота ni /n	Накопичувальна відносна частота Σni /n
						21 25	23	4	4	0,08	0,08
25 29	27	6	10	0,12	0,20
29 33	31	12	22	0,24	0,44
33 37	35	11	33	0,22	0,66
37 41	39	11	44	0,22	0,88
41 45	43	4	48	0,08	0,96
45 49	47	2	50	0,04	1

2) Побудуємо гістограму частот:

3) Побудуємо полігон частот:

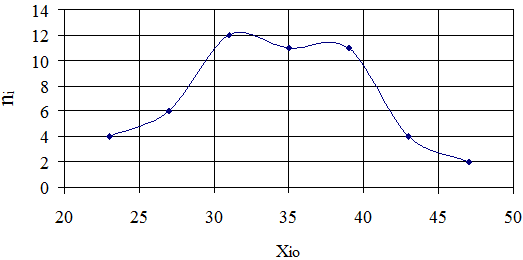
4) Емпірична функція розподілу визначається значеннями накопичувальних відносних частот:

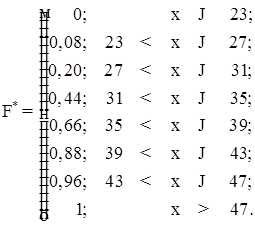
5) Графік розподілу емпіричної функції:

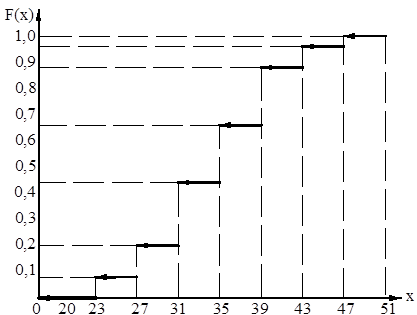
6) Знайдемо методом творів вибіркову середню і вибіркову дисперсію по заданому розподілу вибірки об'єму n=50:

Середина інтервалу xi 0	23	27	31	35	39	43	47
Частота ni	4	6	12	11	11	4	2

6.1) Складемо заповнимо таблицю:

хi 0	ni	Ui	ni ×Ui	ni ×Ui 2	ni ×(Ui +1)2
23	4	-2	-8	16	4
27	6	-1	-6	6	0
31	12	0	0	0	12
35	11	1	11	11	44
39	11	2	22	44	99
43	4	3	12	36	64
47	2	4	8	32	50
39	145	273

6.2) Обчислимо умовні моменти 1-го і 2-го порядку:

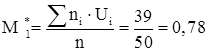
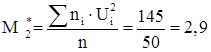
6.3) Знайдемо крок h (різниця між сусідніми інтервалами): .

6.4) Обчислимо шукані, вибіркові, середню дисперсію, враховуючи що помилковий нуль :

3) РОЗРАХУНКОВА РОБОТА №2

“МЕТОД НАЙМЕНЬШИХ КВАДРАТІВ”

За наданими статистичними даними підібрати емпіричну функцію, якщо вона не задана, та:

1. Побудувати діаграму розсіювання.

2. Записати емпіричну функцію.

3. Записати систему нормальних рівнянь.

4. Скласти розрахункову таблицю.

5. Вирішити отриману систему й записати емпіричну функцію зі знайденими параметрами.

Уважаючи, що залежність між змінними й має вигляд , знайти оцінки параметрів по наступних вибірках:

	1	3	4	2	5	7	8	9
	80	90	120	100	110	150	160	130

РОЗВ’ЯЗАННЯ

По вибірці спостережень побудуємо в системі координат и діаграму розсіювання, тобто побудуємо крапки:

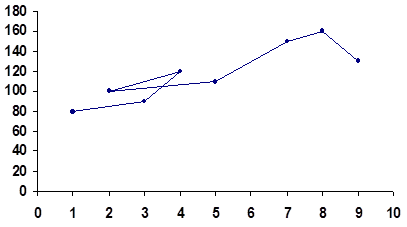
Аналіз дослідницьких даних показує, що в якості емпіричної (підібраної) функції можна використати функцію . Необхідно знайти параметри а й b, для чого застосуємо МНК. Тоді для визначення параметрів а й b будемо мати систему нормальних рівнянь:

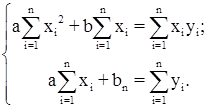
Для зручності обчислень складемо наступну розрахункову таблицю ():

1	1	80	1	80
2	3	90	9	270
3	4	120	16	480
4	2	100	4	200
5	5	110	25	550
6	7	150	49	1050
7	8	160	64	1280
8	9	130	81	1170

Підставимо дані останнього рядка таблиці в нормальну систему рівнянь:

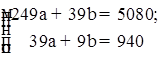
Вирішуючи систему, одержимо .

5) Підставляючи ці значення параметрів, одержимо емпіричну функцію:

6) РОЗРАХУНКОВА РОБОТА №3

“ЗНАХОДЖЕННЯ ВИБІРКОВОГО КОЕФІЦІЕНТА КОРЕЛЯЦІЇ ТА ПРЯМИХ ЛІНІЙ РЕГРЕСІЇ”

Розподіл 40 заводів кольорової металургії за середньодобовим виробленням металу (тис.т) та затратами електроенергії на 1т. 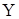(тис. кВт×год) дано у таблиці:

	10-15	15-20	20-25	25-30	30-35
2,0-2,5	6	6
2,5-3,0	6	6	12
3,0-3,5	6	4	10
3,5-4,0	2	4	2	8
4,0-4,5	4	4
	6	4	8	10	12	40

За відповідним рівнянням регресії оцінити середні затрати електроенергії на 1 тн. металу тих заводів, у яких середньодобове вироблення металу складає 22,5 тис.т., та порівняти їх з відповідним груповим середнім.

Надано таблицю, яка визначає деякий неперервний розподіл. За цим розподілом треба утворити дискретний розподіл, взявши значеннями і середини відповідних інтервалів і припускаючи, що між і існує лінійна кореляційна залежність, виконати таку роботу:

1. Обчислити коефіцієнт кореляції та проаналізувати тісноту та напрям зв'язку між і .

2. Скласти рівняння прямих регресії на та на .

3. Обчислити для даного значення однієї змінної відповідне значення іншої, використавши для цього одне з одержаних рівнянь регресії (підхоже) та порівняти це значення з відповідним груповим середнім (це останнє завдання подано разом з кореляційною таблицею).

РОЗВ’ЯЗАННЯ

1) Перейдемо до дискретних розподілів, тобто значення змінних Х и Y приймемо середини відповідних інтервалів:

	12,5	17,5	22,5	27,5	32,5
2,25	6	6
2,75	6	6	12
3,25	6	4	10
3,75	2	4	2	8
4,25	4	4
	6	4	8	10	12	40

2) Для обчислення вибіркового коефіцієнта кореляції потрібно обчислити вираження , для чого скласти кореляційну таблицю в умовних варіантах.

За хибний нуль узята варіанта , а за хибний нуль узята варіанта , які розташовані приблизно в серединах відповідних варіаційних рядів.

3) У кожній клітці, у якій частота , записуємо в правому верхньому куті добуток частоти на .

4) Знаходимо суму всіх чисел, що коштують у правих кутах кліток одного рядка й записуємо її в клітку стовпця .

5) Множимо варіанту на й отриманий добуток записуємо в останню клітку того ж рядка.

6) З метою контролю аналогічні обчислення робимо по стовпцях, причому добуток записуємо в лівому нижньому куті кожної клітки із частотами , після чого їх складаємо й отриману суму записуємо в рядок .

Потім множимо варіанту и на й результат записуємо в останньому рядку.

	-2			-1			0			1			2
-2	-12	6	12	6	12	-24
-1	-6	6	6	-6	6	12	12	18	-18
0	0	6	0	0	4	4	10	4	0
1	2	2	-4	4	4	-4	2	2	0	8	-8	-8
2	8	4	-8	4	-8	-16
	6	4	8	10	12	40
	10			4			2			-6			-18
	-20			-4			0			-6			-36			-66

7) Обчислюємо й :

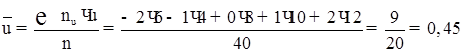
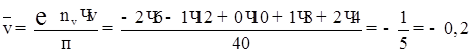
8) Обчислюємо допоміжні величини й :

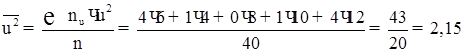
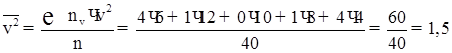
9) Обчислимо й :

10) Шуканий вибірковий коефіцієнт кореляції:

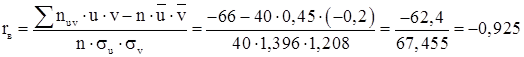
Тому що , цей зв'язок зворотній.

11) Вибіркове рівняння прямої лінії регресії Y на Х має вигляд:

.

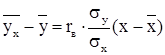Обчислимо , , , :

12) Рівняння прямої лінії регресії Y на Х:

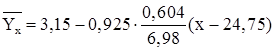
13) Рівняння прямої лінії регресії Х на Y:

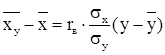
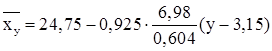
14) За відповідним рівнянням регресії середнє значення затрат електроенергії на 1 тн. металу тих заводів, у яких середньодобове вироблення металу складає 22,5 тис.т., складає:

Якщо скористатися безпосередньо таблицею, то

Як видно, узгодження розрахункового і спостережуваного умовних середніх – задовільне.