Название: Задачи и примеры их решения по теории вероятности

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 77.38 Kb

Скачать файл: referat.me-218182.docx

Краткое описание работы: Вариант 3. 1. Решите уравнение Решение По определению Тогда и уравнение принимает вид откуда получаем Так как m может быть только натуральным числом, то значение

Задачи и примеры их решения по теории вероятности

Вариант 3.

1. Решите уравнение

Решение

По определению

.

Тогда и уравнение принимает вид или откуда получаем и

Так как m может быть только натуральным числом, то значение отбрасываем.

Ответ: .

2. В урне находится 12 белых и 8 черных шаров. Найти вероятность того, что два одновременно изъятых наудачу шара будут черными

Решение

При выборе двух шаров из 20 существует различных вариантов, где , тогда

Определим благоприятных исходов, т.е. извлечены два черных шара. Два черных шара из 8 можно выбрать способами следовательно, число благоприятных исходов

.

Искомая вероятность, согласно классическому определению вероятности, равна отношению числа благоприятных исходов к числу всех исходов:

.

Ответ: .

3. Найдите вероятность того, что наудачу взятое двузначное число окажется кратным либо 4, либо 5, либо тому и другому

Решение

Воспользуемся классическим определением вероятности. Двузначные числа начинаются с 10 и заканчиваются 99 и всего их 90, т.е. N= 90. Теперь посчитаем, сколько у нас чисел кратных либо 4, либо 5, либо тому и другому.

Число кратное 4-м имеет вид , кратное 5 , кратное 4 и 5 .

В интервале от 10 до 99 всего числа кратных четырем (2 кратных до десяти), чисел кратных пяти (1 кратное до 10) и числа кратных и четырем и пяти.

Так как множество чисел кратных 4 и множество чисел кратных 5 не пересекаются, то всего получается 22 + 18 = 40 чисел удовлетворяющих необходимому нам условию, причем числа кратные и четырем и пяти уже входят в эти 40 чисел. В итоге получаем, что вероятность того, что наудачу взятое двузначное число окажется кратным либо 4, либо 5, либо тому и другому равна .

Ответ: .

4. В партии 10 деталей, из которых 8 стандартные. Из этой коробки наудачу извлекается 2 детали. Х – число стандартных деталей. Найти закон распределения, функцию распределения дискретной случайной величины Х, а также основные числовые характеристики

Решение

Среди 2-х извлеченных деталей может быть 0, 1 или 2 стандартные.

Найдем вероятность каждого исхода.

0 стандартных:

1 стандартная:

2 стандартных:

Закон распределения принимает вид:

Х	0	1	2
р

Запишем функцию распределения полученной случайной величины Х:

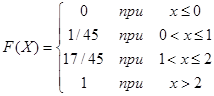
Математическое ожидание М(Х) дискретной случайной величины находится по формуле:

, и подставляя данные, получим:

Дисперсию дискретной случайной величины можно вычислить по формуле:

, и, подставляя данные, получим:

Среднеквадратичное отклонение:

s(Х)=

Ответ: ; ; .

5. По данной выборке постройте полигон. Найти эмпирическую функцию.

Хi	2	5	7	8
Ni	1	3	2	4

Решение

Построим полигон частот – ломаную, соединяющую точки с координатами (Х_i ; N_i ).

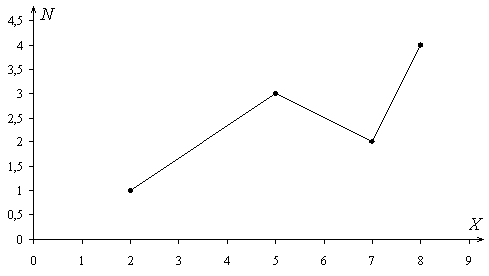
Объем выборки равен N = 1 + 3 + 2 + 4 = 10.

Найдем относительные частоты и составим эмпирическую функцию распределения:

Хi	2	5	7	8
wi	0,1	0,3	0,2	0,4

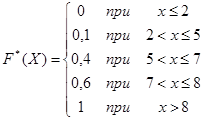
Ответ: решение выше.