Название: Основы математического анализа
Вид работы: контрольная работа
Рубрика: Математика
Размер файла: 154.76 Kb
Скачать файл: referat.me-215219.docx
Краткое описание работы: Основные обозначения и понятия, относящиеся к множествам, операции над ними. Объединение, пересечение и разность двух множеств и непринадлежность к нему элемента. Первая и вторая теорема Вейерштрасса, Ферма и Ролля. Вычисление интеграла вероятности.
Основы математического анализа
1. Множества и операции над множествами
Напомним основные обозначения, понятия, относящиеся к множествам, которых будем придерживаться дальше.
Начнем с основного понятия, которое встречается практически в каждом разделе математики - это понятие множества.
Множество - это совокупность, набор элементов, объединенных общими свойствами.
Множества обозначаются заглавными латинскими буквами ![]() , а элементы множества строчными латинскими буквами
, а элементы множества строчными латинскими буквами ![]() .
.
Запись ![]() означает, что есть множество
означает, что есть множество ![]() с элементами
с элементами ![]() , которые связаны между собой какой-то функцией
, которые связаны между собой какой-то функцией ![]() .
.
Замечание. Элементы в множество входят по одному разу, т.е. без повторений.
Основные операции:
1. Принадлежность элемента множеству:
![]()
где ![]() -- элемент и
-- элемент и ![]() -- множество (элемент
-- множество (элемент ![]() принадлежит множеству
принадлежит множеству ![]() ).
).
2. Непринадлежность элемента множеству:
![]()
где ![]() -- элемент и
-- элемент и ![]() -- множество (элемент
-- множество (элемент ![]() не принадлежит множеству
не принадлежит множеству ![]() ).
).
3. Объединение множеств: ![]() .
.
Объединением двух множеств![]() и
и ![]() называется множество
называется множество ![]() , которое состоит из элементов множеств
, которое состоит из элементов множеств ![]() и
и ![]() , т.е.
, т.е.
![]() или
или![]()
4. Пересечение множеств: ![]() .
.
Пересечением двух множеств![]() и
и ![]() называется множество
называется множество ![]() , которое состоит из общих элементов множеств
, которое состоит из общих элементов множеств ![]() и
и ![]() , т.е.
, т.е.
![]() и
и![]()
5. Разность множеств: ![]() .
.
Разностью двух множеств![]() и
и ![]() , например, множество
, например, множество ![]() минус множество
минус множество ![]() , называется множество
, называется множество ![]() , которое состоит из элементов множества
, которое состоит из элементов множества ![]() , которых нет в множестве
, которых нет в множестве ![]() , т.е.
, т.е.
![]() и
и![]()
6. Симметрическая разность множеств:
![]() .
.
Симметрической разностью двух множеств![]() и
и ![]() называется множество
называется множество ![]() , которое состоит из не общих элементов множеств
, которое состоит из не общих элементов множеств ![]() и
и ![]() , т.е.
, т.е.
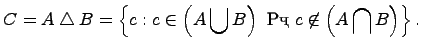
7. Дополнение множества: ![]() .
.
Если предположим, что множество ![]() является подмножеством некоторого универсального множества
является подмножеством некоторого универсального множества ![]() , тогда определяется операция дополнения:
, тогда определяется операция дополнения:
![]() и
и![]()
8. Вхождение одного множества в другое множество: ![]() .
.
Если любой элемент множества ![]() является элементом множества
является элементом множества ![]() , то говорят, что множество
, то говорят, что множество ![]() есть подмножество множества
есть подмножество множества ![]() (множество
(множество ![]() входит в множество
входит в множество ![]() ).
).
9. Не вхождение одного множества в другое множество: ![]() .
.
Если существует элемент множества ![]() , который не является элементом множества
, который не является элементом множества ![]() , то говорят, что множество
, то говорят, что множество ![]() не подмножество множества
не подмножество множества ![]() (множество
(множество ![]() не входит в множество
не входит в множество ![]() ).
).
2. Первая и вторая теорема Вейерштрасса
Теорема (первая теорема Вейерштрасса)Если функция непрерывна на сегменте, то она ограничена на нем.Доказательство: методом от противного, воспользуемся свойством замкнутости сегмента [a;b]. Из любой последовательности (xn) этого сегмента можем выделить подпоследовательность xnk, сходящуюся к x0∈[a;b] .Пусть f не ограничена на сегменте [a;b], например, сверху, тогда для всякого натуральногоn∈Nнайдется точка xn∈[a;b] , что f(xn)>n. Придавая n значения 1,2,3,{ldots}, мы получим последовательность (xn) точек сегмента [a;b], для которых выполнено свойство f(x1)>1,f(x2)>2,f(x3)>3,...,f(xn)>n... Последовательность (xn) ограничена и поэтому из нее по теореме можно выделить подпоследовательность(xnk) , которая сходится к точке x0∈[a;b] : limk→∞xnk=x0 (1)Рассмотрим соответствующую последовательность (f(xnk)) . С одной стороны f(xnk)>nkи поэтому limk→∞f(xnk)=+∞(2),С другой стороны, учитывая определение непрерывной функции по Гейне из (1) будем иметь limk→∞f(xnk)=f(x0) (3)Получаем равенства (2) и (3) противоречат теореме (о единственности предела). Это противоречие и доказывает справедливость теоремы. Аналогично доказывается ограниченность функции снизу. Ч.Т.Д.
Замечание 1Таким образом, если f непрерывна на [a;b], то ее множество значений ограничено и поэтому существует конечные верхняя и нижняя грань функции.c=infx∈[a;b]f(x),d=supx∈[a;b]f(x), но открыт вопрос о достижении функции своих граней.Замечание 2Если слово сегмент в условии теоремы заменить словом интервал или полуинтервал, то теорема может и нарушиться. Пример, y=tgx,tgx∈C((−2π;2π)) , но функция не ограничена на этом интервале.
Теорема (вторая теорема Вейерштрасса)Если функция непрерывна на сегменте, то она достигает на нем своих граней (т.е. непрерывная на сегменте функция принимает свое наибольшее и наименьшее значения).Доказательство: Пусть f(x)∈C([a;b]) , c=infx∈[a;b]f(x), d=supx∈[a;b]f(x). По первой теореме Вейерштрасса c,d∈R. Докажем, что f достигает на [a;b] своих граней, т.е. найдутся такие точки x1,x2∈[a;b] , чтоf(x1)=c,f(x2)=d.Докажем, например, существование точки x2.
По определению верхней грани имеем (∀x∈[a;b])(f(x)=d) . Предположим противное, т.е. точки x2, в которой f(x2)=dна [a;b], тогда на [a;b] выполняется условиеf(x)<d или d−f(x)>0 . Далее введем вспомогательную функцию ϕ(x)=1d−f(x). ϕ(x)на [a;b] положительна и непрерывна (как отношение двух непрерывных на [a;b] функций и d−f(x)/=0) , поэтому по первой Т. Вейерштрасса ϕ(x)на [a;b] ограничена. Это означает, что при некотором М>0 (∀x∈[a;b])(0<1d−f(x)≤M) , отсюда имеем f(x)≤d−1M<d. Полученное неравенство противоречит тому, что d является верхней гранью функции f(x) на [a;b], т.е. наименьшим из верхних границ. Полученное противоречие и означает существование точки x2 такой, что f(x2)=d.
Аналогично доказывается существование точки x1∈[a;b] , такой что f(x1)=c.
СледствиеЕсли f непрерывна и непостоянна на [a;b], то образ этого отрезка [a;b] при отображении f будет так же отрезок, т.е. непрерывный непостоянный образ отрезка есть отрезок.Доказательство: В самом деле образом отрезка [a;b] при отображении f будет отрезок [с;d], где c=inf[a;b]f(x)=min[a;b]f(x), а d=sup[a;b]f(x)=max[a;b]f(x), что следует из второй теоремы Больцано-Коши и второй теоремы Вейерштрасса Ч.Т.Д.
3. Теорема Ферма и Ролля
Пусть функция f(x) имеет на множестве E точку экстремума x₀?E, причём множество E содержит некоторую β- окрестность, что E=(x- β;x+ β) точки x. Тогда либо f(x) имеет в точке x производную, равную 0, то есть f´(x)=0 , либо производная в точке x не существует. Теорема Ролля Если функция f(x) непрерывна на отрезке (a;b), дифференцируема во всех внутренних точках этого отрезка и на концах x=a и x=b обращается в нуль, [f(a)=f(b)=0], то внутри отрезка (a;b) существует п окрпйней мере одна тоска x=c, a<c<b, в которой производная f´(x) обращается в нуль, т.е. f´(c)=0
Метод математической индукции
Метод математической индукции является важным способом доказательства предложений (утверждений), зависящих от натурального аргумента.
Метод математической индукции состоит в следующем:
Предложение (утверждение) P(n), зависящее от натурального числа n, справедливо для любого натурального n если:
1. P(1) является истинным предложением (утверждением);
2. P(n) остается истинным предложением (утверждением), если n увеличить на единицу, то есть P(n + 1) - истинное предложение (утверждение).
Таким образом метод математической индукции предполагает два этапа:
1. Этап проверки: проверяется, истинно ли предложение (утверждение) P(1).
2. Этап доказательства: предполагается, что предложение P(n) истинно, и доказывается истинность предложения P(n + 1) (n увеличено на единицу).
Замечание 1. В некоторых случаях метод математической индукции используется в следующей форме:
Пусть m - натуральное число, m > 1 и P(n) - предложение, зависящее от n, n ≥ m.
Если
1. P(m) справедливо;
2. P(n) будучи истинным предложением, влечет истинность предложения P(n + 1) для любого натурального n, n ≥ m, тогда P(n) - истинное предложение для любого натурального n, n ≥ m.
В дальнейшем рассмотрим примеры применения метода математической индукции.
Пример 1. Доказать следующие равенства
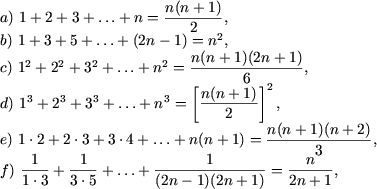
g) формула бинома Ньютона:
![]()
где n Î N.
Решение. a) При n = 1 равенство примет вид ![]() 1=1, следовательно, P(1) истинно. Предположим, что данное равенство справедливо, то есть, имеет место
1=1, следовательно, P(1) истинно. Предположим, что данное равенство справедливо, то есть, имеет место
![]() .
.
Следует проверить (доказать), что P(n + 1), то есть
![]()
истинно. Поскольку (используется предположение индукции)
![]()
получим
![]()
то есть, P(n + 1) - истинное утверждение.
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
Замечание 2. Этот пример можно было решить и иначе. Действительно, сумма 1 + 2 + 3 + ... + n есть сумма первых n членов арифметической прогрессии с первым членом a1
= 1 и разностью d = 1. В силу известной формулы ![]() , получим
, получим
![]()
b) При n = 1 равенство примет вид: 2·1 - 1 = 12 или 1=1, то есть, P(1) истинно. Допустим, что имеет место равенство
1 + 3 + 5 + ... + (2n - 1) = n2
и докажем, что имеет место P(n + 1):
1 + 3 + 5 + ... + (2n - 1) + (2(n + 1) - 1) = (n + 1)2
или
1 + 3 + 5 + ... + (2n - 1) + (2n + 1) = (n + 1)2 .
Используя предположение индукции, получим
1 + 3 + 5 + ... + (2n - 1) + (2n + 1) = n2 + (2n + 1) = (n + 1)2 .
Таким образом, P(n + 1) истинно и, следовательно, требуемое равенство доказано.
Замечание 3. Этот пример можно решить (аналогично предыдущему) без использования метода математической индукции.
c) При n = 1 равенство истинно: ![]() 1=1. Допустим, что истинно равенство
1=1. Допустим, что истинно равенство
![]()
и покажем, что
![]()
то есть истинность P(n) влечет истинность P(n + 1). Действительно,
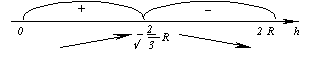
и, так как 2n2 + 7n + 6 = (2n + 3)(n + 2), получим
![]()
и, следовательно, исходное равенство справедливо для любого натурального n.
d) При n = 1 равенство справедливо: ![]() 1=1. Допустим, что имеет место
1=1. Допустим, что имеет место
![]()
и докажем, что
![]()
Действительно,
e) Утверждение P(1) справедливо: ![]() 2=2. Допустим, что равенство
2=2. Допустим, что равенство
![]()
справедливо, и докажем, что оно влечет равенство
![]()
Действительно,
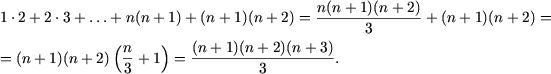
Следовательно, исходное равенство имеет место для любого натурального n.
f) P(1) справедливо: ![]() 1
/3
= 1
/3
. Пусть имеет место равенство P(n):
1
/3
= 1
/3
. Пусть имеет место равенство P(n):
![]() .
.
Покажем, что последнее равенство влечет следующее:
![]()
Действительно, учитывая, что P(n) имеет место, получим
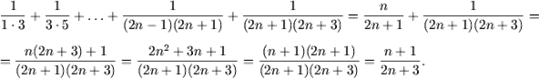
Таким образом, равенство доказано.
g) При n = 1 имеем a + b = b + a и, следовательно, равенство справедливо.
Пусть формула бинома Ньютона справедлива при n = k, то есть,
![]()
Тогда
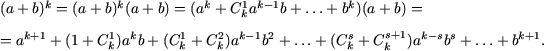
Используя равенство ![]() получим
получим
![]()
Пример 2. Доказать неравенства
a) неравенство Бернулли: (1 + )n ≥ 1 + n, > -1, n N.
b) x1
+ x2
+ ... + xn
≥ n, если x1
x2
· ... ·xn
= 1 и xi
> 0, ![]() .
.
c) неравенство Коши относительно среднего арифемтического и среднего геометрического
![]() где xi
> 0,
где xi
> 0, ![]() , n ≥ 2.
, n ≥ 2.
d) sin2n a + cos2n a ≤ 1, n ÎN.
e) ![]()
f) 2n > n3 , n Î N, n ≥ 10.
Решение. a) При n = 1 получаем истинное неравенство
1 + a ≥ 1 + a.
Предположим, что имеет место неравенство
(1 + a)n ≥ 1 + na (1)
и покажем, что тогда имеет место и
(1 + a)n + 1 ≥ 1 + (n + 1)a.
, a > -1 a + 1 > 0, (1) (a + 1),
(1 + a)n (1 + a) ≥ (1 + na)(1 + a)
(1 + a)n + 1 ≥ 1 + (n + 1)a + na2
na2 ≥ 0, ,
(1 + a)n + 1 ≥ 1 + (n + 1)a + na2 ≥ 1 + (n + 1)a.
Таким образом, если P(n) истинно, то и P(n + 1) истинно, следовательно, согласно принципу математической индукции, неравенство Бернулли справедливо.
b) При n = 1 получим x1 = 1 и, следовательно, x1 ≥ 1 то есть P(1) - справедливое утверждение. Предположим, что P(n) истинно, то есть, если adica, x1 ,x2 ,...,xn - n положительных чисел, произведение которых равно единице, x1 x2 ·...·xn = 1, и x1 + x2 + ... + xn ≥ n.
Покажем, что это предложение влечет истинность следующего: если x1 ,x2 ,...,xn ,xn +1 - (n + 1) положительных чисел, таких, что x1 x2 ·...·xn ·xn +1 = 1, тогда x1 + x2 + ... + xn + xn + 1 ≥ n + 1.
Рассмотрим следующие два случая:
1) x1 = x2 = ... = xn = xn +1 = 1. Тогда сумма этих чисел равна (n + 1), и требуемое неравество выполняется;
2) хотя бы одно число отлично от единицы, пусть, например, больше единицы. Тогда, поскольку x1 x2 · ... ·xn ·xn + 1 = 1, существует еще хотя бы одно число, отличное от единицы (точнее, меньше единицы). Пусть xn + 1 > 1 и xn < 1. Рассмотрим n положительных чисел
x1 ,x2 ,...,xn -1 ,(xn ·xn +1 ).
Произведение этих чисел равно единице, и, согласно гипотезе,
x1 + x2 + ... + xn -1 + xn xn + 1 ≥ n.
Последнее неравенство переписывается следующим образом:
x1 + x2 + ... + xn -1 + xn xn +1 + xn + xn +1 ≥ n + xn + xn +1
или
x1 + x2 + ... + xn -1 + xn + xn +1 ≥ n + xn + xn +1 - xn xn +1 .
Поскольку
(1 - xn )(xn +1 - 1) > 0,
n + xn + xn +1 - xn xn +1 = n + 1 + xn +1 (1 - xn ) - 1 + xn = = n + 1 + xn +1 (1 - xn ) - (1 - xn ) = n + 1 + (1 - xn )(xn +1 - 1) ≥ n + 1.
Следовательно,
x1 + x2 + ... + xn + xn +1 ≥ n+1,
то есть, если P(n) справедливо, то и P(n + 1) справедливо. Неравенство доказано.
Замечание 4. Знак равенства имеет место тогда и только тогда, когда x1 = x2 = ... = xn = 1.
c) Пусть x1 ,x2 ,...,xn - произвольные положительные числа. Рассмотрим следующие n положительных чисел:
![]()
Поскольку их произведение равно единице:
![]()
согласно ранее доказанному неравенству b), следует, что
![]()
откуда
![]()
Замечание 5. Равенство выполняется если и только если x1 = x2 = ... = xn .
d) P(1) - : sin2 a + cos2 a = 1. , P(n) - :
sin2n a + cos2n a ≤ 1
, P(n + 1). ,
sin2(n + 1) a + cos2(n + 1) a = sin2n asin2 a + cos2n acos2 a < sin2n a + cos2n a ≤ 1
( sin2 a ≤ 1, cos2 a < 1, : cos2 a ≤ 1, sin2 a < 1). , n Î N sin2n a + cos2n ≤ 1 n = 1.
e) При n = 1 утверждение справедливо: ![]() 1 < 3
/2
.
1 < 3
/2
.
Допустим, что ![]() и докажем, что
и докажем, что
![]()
Поскольку
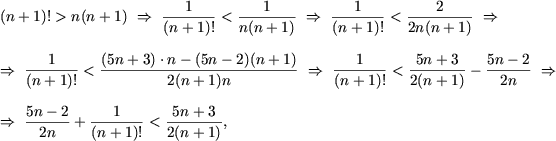
учитывая P(n), получим
![]()
f) Учитывая замечание 1, проверим P(10): 210 > 103 , 1024 > 1000, следовательно, для n = 10 утверждение справедливо. Предположим, что 2n > n3 (n > 10) и докажем P(n + 1), то есть 2n+1 > (n + 1)3 .
Поскольку при n > 10 имеем ![]() или
или ![]() , следует, что
, следует, что
2n3 > n3 + 3n2 + 3n + 1 илиn3 > 3n2 + 3n + 1.
Учитывая неравенство (2n > n3 ), получим
2n+1 = 2n ·2 = 2n + 2n > n3 + n3 > n3 + 3n2 + 3n + 1 = (n + 1)3 .
Таким образом, согласно методу математической индукции, для любого n Î N, n ≥ 10 2n > n3 .
3., n Î N
a) n(2n2 - 3n + 1) делится на 6,
b) 62n-2 + 3n+1 + 3n-1 делится на 11.
Решение. a) P(1) - истинное утверждение (0 делится на 6). Пусть P(n) справедливо, то есть n(2n2 - 3n + 1) = n(n - 1)(2n - 1) делится на 6. Покажем, что тогда имеет место P(n + 1), то есть, (n + 1)n(2n + 1) делится на 6. Действительно, поскольку
n(n + 1)(2n + 1) = n(n - 1 + 2)(2n - 1 + 2) = (n(n - 1) + 2n)(2n - 1 + 2) =
= n(n - 1)(2n - 1) + 2n(n - 1) + 2n(2n + 1) = n(n - 1)(2n - 1) + 2n·3n =
= n(n - 1)(2n - 1) + 6n2
и, как n(n - 1)(2n - 1), так и 6n2 делятся на 6, тогда и их сумма n(n + 1)(2n + 1) делится 6.
Таким образом, P(n + 1) - справедливое утверждение, и, следовательно, n(2n2 - 3n + 1) делится на 6 для любого n N.
b) Проверим P(1): 60 + 32 + 30 = 11, следовательно, P(1) - справедливое утверждение. Следует доказать, что если 62n-2 + 3n+1 + 3n-1 делится на 11 (P(n)), тогда и 62n + 3n+2 + 3n также делится на 11 (P(n + 1)). Действительно, поскольку
62n + 3n+2 + 3n = 62n-2+2 + 3n+1+1 + 3n-1+1 =
= 62 ·62n-2 + 3·3n+1 + 3·3n-1 = 3·(62n-2 + 3n+1 + 3n-1 ) + 33·62n-2
и, как 62n-2 + 3n+1 + 3n-1 , так и 33·62n-2 делятся на 11, тогда и их сумма 62n + 3n+2 + 3n делится на 11. Утверждение доказано.
Несобственные интегралы
Пусть функция f(x) определена на полуинтервале (a, b] и ![]() ,
, ![]() ; кроме того
; кроме того
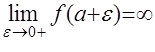
Определение: Несобственным интегралом 1рода от f(x) на (a, b] называется предел:
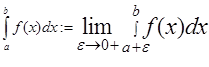
если этот предел существует. В этом случае говорят, что несобственный интеграл сходится.
Пример:
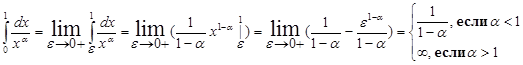
Если a = 1, то
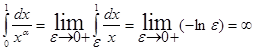
Следовательно, при a < 1 интеграл
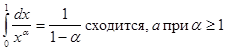
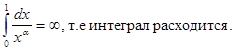
Аналогично определяется несобственный интеграл, если
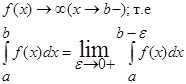
Определение несобственного интеграла 2 рода:
Пусть ![]() :
: ![]() и существует предел:
и существует предел:
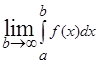
Тогда этот предел называется несобственным интегралом 2 рода, т.е.
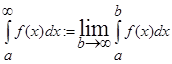
Пример:
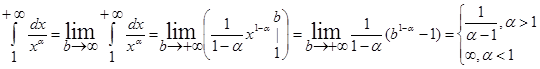
Если a = 1, то
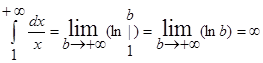
Следовательно, несобственный интеграл
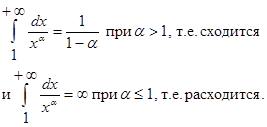
Для исследования сходимости и расходимости несобственных интегралов применяется признак сравнения:
Пусть функция f(x) и g(x) удовлетворяют неравенству: ![]() и несобственный интеграл
и несобственный интеграл 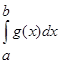 сходится. Тогда сходится и несобственный интеграл
сходится. Тогда сходится и несобственный интеграл 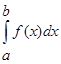 .
.
Доказательство: В силу сходимости 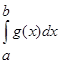 по критерию Коши для функции
по критерию Коши для функции ![]() , выполняется неравенство
, выполняется неравенство 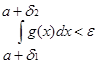 . Но тогда, ввиду неравенств:
. Но тогда, ввиду неравенств: ![]() аналогично неравенство будет справедливо и для функции f(x), т.е.
аналогично неравенство будет справедливо и для функции f(x), т.е.
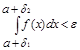
Следовательно, по критерию Коши существует предел:
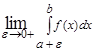 ,
,
т.е. этот интеграл сходится.
Замечание1: Аналогичный признак сравнения справедлив и для несобственных интегралов 2 рода.
Замечание2: Отрицанием признака сравнения будет следующее утверждение: если несобственный интеграл 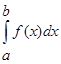 расходится, то расходится и несобственный интеграл
расходится, то расходится и несобственный интеграл
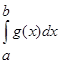 .
.
Эйлеровы интегралы G(a) и B(a, b).
Определим функцию G(a) равенством:
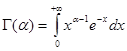 .
.
Покажем, что интеграл сходится при a > 0. Представим этот интеграл в виде суммы двух интегралов:
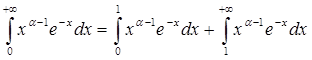
и докажем сходимость каждого из этих интегралов при a > 0.
Обозначим
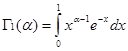 и
и ![]() .
.
Если xÎ(0, 1], то: ![]() . Так как интеграл
. Так как интеграл 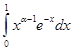 , как это было доказано выше сходится при 1 - a< 1, т.е. при a>0, то по признаку сравнения интеграл
, как это было доказано выше сходится при 1 - a< 1, т.е. при a>0, то по признаку сравнения интеграл ![]() сходится при a>0. Если xÎ[1, +
сходится при a>0. Если xÎ[1, + ![]() ) , то для некоторой константы c>0 выполняется неравенство:
) , то для некоторой константы c>0 выполняется неравенство: ![]() .
.
Заметим, что
![]() ,
,
т.е. этот интеграл сходится при любых aÎR. Следовательно, функция Эйлера G(a) = G1 (a) + G2 (a) определена для всех a>0.
Далее, определим функцию
B(a, b) = 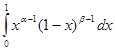
и докажем, что эта функция определена для любых a>0 и b>0.
Обозначим:
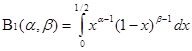 и
и 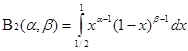 .
.
Если xÎ(0, 1/2], то ![]() . Интеграл
. Интеграл 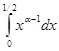 сходится по признаку сравнения 1 - a<1, т.е. при a>0 и при любых значениях b. Заметим, что, если в интеграле B2
(a, b) сделать замену t = 1 – x, то мы B1
(b, a), который, как мы выяснили, сходится при b>0 и при любых a.
сходится по признаку сравнения 1 - a<1, т.е. при a>0 и при любых значениях b. Заметим, что, если в интеграле B2
(a, b) сделать замену t = 1 – x, то мы B1
(b, a), который, как мы выяснили, сходится при b>0 и при любых a.
Следовательно, функция Эйлера B(a, b) = B1 (a, b) + B2 (a, b) определена для любых a>0 и b>0. Отметим (без доказательства) следующие свойства интегралов Эйлера:
1) G(1) = 1
2) G(a + 1) = aG(a), a>0
3) G(n + 1) = n!, nÎN
4) G(a)G(1 - a) =![]() , 0<a<1
, 0<a<1
5) G(1/2) = ![]()
6) B(a, b) = ![]()
Пример:
Вычислить интеграл вероятности
![]() .
.
В силу чётности функции ![]() интеграл вероятности можно представить в виде:
интеграл вероятности можно представить в виде:
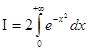 .
.
Сделав в этом интеграле замену t = x2 , получим следующий интеграл:
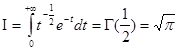
Похожие работы
-
Алгебра и алгебраические системы
Рассматриваются бинарные и n-местные операции, виды бинарных операций, вводятся понятия алгебры, подалгебры, алгебраической системы, приводятся примеры.
-
Множества Операции над множествами
РЕФЕРАТ Множества. Операции над множествами СОДЕРЖАНИЕ Способы задания множества Включение и равенство множеств Диаграммы Эйлера-Венна Операции над множествами
-
Простое доказательство великой теоремы Ферма
Представление великой теоремы Ферма как диофантового уравнения. Использование для ее доказательства метода замены переменных. Невозможность решения теоремы в целых положительных числах. Необходимые условия и значения чисел для решения, анализ уравнений.
-
Конспект по дискретной математики
Дискретная математика Введение Общество 21в. – общество информационное. Центр тяжести в решении задач переместился от задач вычислительной математики к задачам на дискретных структурах. Математика нужна не как метод расчета, а как метод мышлению средство формирования и организации…
-
Задачи по Высшей математике
Вариант № 2 Задача 1 Найти объединение и пересечение множеств А и В, если А ={1;3;5} и B={0;1;2;-3;4;-5}. Решение: Объединение множеств А и В А В= {0;1;2;3;5;-3;4;-5},
-
Доказательство Великой теоремы Ферма для степени n 3
Файл: FERMA-n3-algo © Н. М. Козий, 2009 Украина, АС № 28607 ДОКАЗАТЕЛЬСТВО ВЕЛИКОЙ ТЕОРЕМЫ ФЕРМА ДЛЯ ПОКАЗАТЕЛЯ СТЕПЕНИ n=3 Великая теорема Ферма для показателя степени n=3 формулируется следующим образом: диофантово уравнение:
-
Исследование функций
Основные теоремы дифференциального исчисления: Ферма, Ролля, Коши, Лагранжа и их доказательство. Локальные экстремумы функции, исследование ее на выпуклость и вогнутость, понятие точки перегиба. Асимптоты и общая схема построения графика функции.
-
Множества и операции над ними
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ ТАВРИЧЕСКОЕ ПРДСТАВИТЕЛЬСТВО ОТКРЫТОГО МЕЖДУНАРОДНОГО УНИВЕРСИТЕТА РАЗВИТИЯ ЧЕЛОВЕКА (УКРАИНА) Реферат
-
Элементы комбинаторного анализа
Глава 1 Элементы комбинаторного анализа 1.1. Начальные понятия теории множеств Под множеством понимают объединение в единое целое определенных вполне различаемых объектов. Объекты при этом называют элементами образуемого ими множества.
-
Логика формальная и графическая модель описания изготовления винных изделий
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ Государственный университет информатики и искусственного интеллекта Кафедра системного анализа и моделирования