Название: Рівняння регресії і побудова економетричних моделей
Вид работы: контрольная работа
Рубрика: Математика
Размер файла: 253.75 Kb
Скачать файл: referat.me-215388.docx
Краткое описание работы: ЗМІСТ Завдання 1. Побудова економетричної моделі парної регресії 2 Завдання 2. Побудова економетричної моделі множинної регресії 2 Розв’язання завдання 1. 3
Рівняння регресії і побудова економетричних моделей
ЗМІСТ
Завдання 1. Побудова економетричної моделі парної регресії 2
Завдання 2. Побудова економетричної моделі множинної регресії 2
Розв’язання завдання 1. 3
Розв’язання завдання 2. 8
3. Регресійний аналіз. 8
Завдання 1. Побудова економетричної моделі парної регресії
На основі даних про витрати обігу (залежна змінна) і вантажообігу (незалежна змінна) побудувати економетричну модель:
· оцінити параметри моделі за методом найменших квадратів;
· визначити коефіцієнти кореляції та детермінації;
· оцінити значимість регресійної моделі за критерієм Фішера;
· оцінити значимість параметрів моделі регресії;
· виконати точкове прогнозування yn+1 для ![]() , де р = 0,95;
, де р = 0,95;
· обчислити інтервали довіри для залежної змінної при α = 0,05;
· зробити висновок.
Таблиця 1. Вихідні дані для розрахунку (варіант 9)
| Х (незалежна змінна) |
У (залежна змінна) |
| 0,15 |
1,35 |
| 0,34 |
1,39 |
| 0,09 |
1,27 |
| 0,05 |
1,10 |
| 0,48 |
1,23 |
| 0,41 |
1,39 |
| 0,62 |
1,38 |
| 0,50 |
1,35 |
| 1,2 |
1,24 |
| 0,21 |
1,40 |
Завдання 2. Побудова економетричної моделі множинної регресії
На основі даних таблиці (таблиця 2) спостережень побудувати найкраще рівняння регресії:
· побудувати кореляційну матрицю, використовуючи процедуру Кореляція;
· визначити наявність мультиколінеарності;
· провести регресійний аналіз, використовуючи процедуру Регресія;
· побудувати рівняння регресії і оцінити статистичні характеристики;
· визначити найкраще рівняння регресії.
Таблиця 2
Вихідні дані для розрахунку (варіант 9)
| У |
Х1 |
Х2 |
Х3 |
| 9,4 |
0,23 |
1,35 |
173,9 |
| 9,9 |
0,43 |
1,39 |
162,3 |
| 9,1 |
0,26 |
1,27 |
101,2 |
| 5,5 |
0,43 |
1,10 |
177,8 |
| 6,6 |
0,38 |
1,23 |
93,2 |
| 4,3 |
0,42 |
1,39 |
126,7 |
| 7,4 |
0,30 |
1,38 |
91,8 |
| 6,6 |
0,37 |
1,35 |
70,6 |
| 5,5 |
0,34 |
1,24 |
97,2 |
| 9,4 |
0,23 |
1,40 |
80,3 |
Розв’язання завдання 1 .
Рівняння регресії має наступний вигляд: ŷ![]() . Розрахуємо необхідні для оцінки методом найменших квадратів коефіцієнти b0 і b1. Проміжні розрахунки наведено в Додатку 1.
. Розрахуємо необхідні для оцінки методом найменших квадратів коефіцієнти b0 і b1. Проміжні розрахунки наведено в Додатку 1.
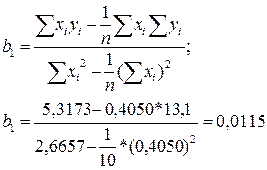
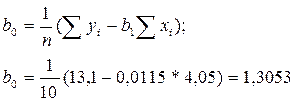
Отже, відповідно до методу найменших квадратів, рівняння регресії має вигляд: ŷ ![]()
Визначимо коефіцієнти кореляції та детермінації.
Коефіцієнт парної детермінації
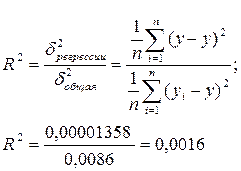
Висновок: коефіцієнт парної детермінації R2 складає 0,0016. Це означає, що тільки 0,16% змін змінної у визначається лінійною залежністю від змінної х. Такий зв’язок дуже малий для подальшого аналізу і не здатний надати точних результатів для подальшого прогнозування.
Для перевірки коефіцієнту детермінації висуваємо гіпотези:
Н0: R2 = 0 (лінійної залежності немає).
Н1: R2 ≠ 0 (лінійна залежність є).
Обираємо рівень значущості α – за умовами він дорівнює 0,05.
α = 0,05.
Визначаємо ступінь свободи k:
k1 = m = 1
k2 = n – 2 = 10 – 2 = 8
n – кількість спостережень; m – кількість пояснювальних змінних.
Скориставшись таблицею Фішера, визначимо, що F0,05 = 5,32.
Определим F-статистику:
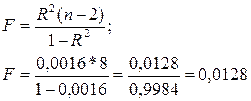
F < F0,05. Отже, гіпотезу R2 ≠ 0 відкидаємо з п’ятивідсотковим ризиком помилитись і приймаємо гіпотезу Н0: R2 = 0. Таким чином, з імовірністю більше 95% можна стверджувати, що між змінними х та у не існує лінійної залежності.
Коефіцієнт кореляції rxy:
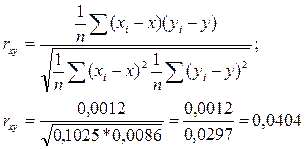
Повинна виконуватись умова ![]() .
.
У нашому випадку (0,0404) 2 ≈ 0,0016 ≈ R2. Приблизна рівність означає, що розрахунки проведено вірно.
Висновок: коефіцієнт кореляції rxy складає 0,0404. Це означає, що між змінними х та у існує дуже слабка лінійна залежність.
Для перевірки надійності коефіцієнту кореляції визначимо t-статистику:
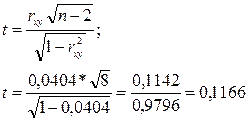
Повинна виконуватись умова ![]() .
.
В нашому випадку (0,1166) 2 ≈ 0,0136 ≈ F. Приблизна рівність (F = 0,0128) означає, що в розрахунках були погрішності, але через їхню незначущість ними можна зневажати.
3. Оцінка значущості параметрів моделі. Побудування інтервалів довіри.
I. Оцінімо параметр b0. Для цього розрахуємо коефіцієнт статистику t0.
b0 = 1,3053
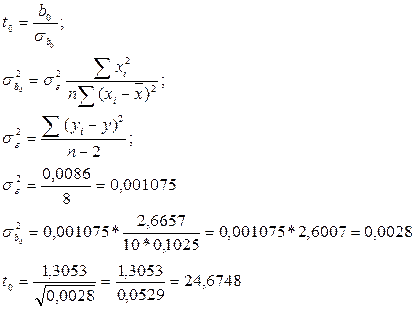 |
Висуваємо гіпотези:
H0: β0 = 0
H1: β0 ≠ 0
Рівень значущості α = 0,05
Кількість ступенів свободи k = n – 2; k = 10 – 2 = 8.
За допомогою таблиці теста Стьюдента визначимо, що t0,05 = 2,31.
![]()
Висновок: за п’ятивідсоткового рівня значущості можна стверджувати, що з імовірністю, більшою за95% оцінка b0 є статистично значущою, що потребує розрахунку інтервалу довіри.
β0 = b0 ± t0,05*σb0 = 1,3053 ± 2,31*0,0529 = 1,3053 ± 0,122199
Р(1,183101< β0 < 1,427499) = (1 – α) *100% = 95%
Таким чином, в генеральній сукупності β0 з імовірністю 95% знаходиться в інтервалі (1,183101; 1,427499).
II. Оцінімо параметр b1.
b1 = 0,0115
Визначимо t-статистику для b1:
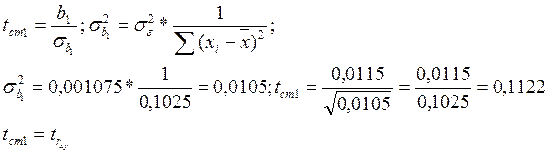
В нашому випадку tст1 ≈ trxy. Приблизна рівність допустима (trxy = 0,1166) і означає, що в розрахунках були погрішності, якими можна зневажати.
Висуваємо гіпотези:
H0: β0 = 0
H1: β0 ≠ 0
tст1 = 0,1122
Рівень значущості α = 0,05.
Кількість ступенів свободи k = n – 2; k = 10 – 2 = 8.
За допомогою таблиці теста Стьюдента визначимо, що t0,05 = 2,31.
tст1< t0,05.
Висновок: за п’ятивідсоткового рівня значущості можна стверджувати, що з імовірністю, більшою за 95%, оцінка параметра b1 не є статистично значущою, звідки робимо висновок, що інтервал довіри не розраховується.
4. Точкове прогнозування yn+1 для ![]() , де р = 0,95.
, де р = 0,95.
ŷn+1 = b0 + b1*xn+1
ŷn+1 = 1,3053 + 0,0115*11 = 1,4318.
Висновок: отже, за прогнозними даними в 11-му періоді значення залежної змінної дорівнюватиме 1,4318. Але, як було вказано раніше, ці прогнозні значення навряд чи можна вважати достовірними, тому що коефіцієнти детермінації та кореляції відповідають дуже слабкому рівню зв’язку між змінними.
Розв’язання завдання 2
1. Кореляційна матриця.
За допомогою Пакету аналізу Excel побудуємо кореляційну матрицю, використовуючи операцію Кореляція (рис.1).
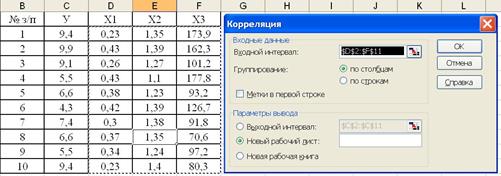
Рис.1. Процес побудови кореляційної матриці.
Таблиця 1. Кореляційна матриця Excel
| Стовпчик 1 |
Стовпчик 2 |
Стовпчик 3 |
|
| Стовпчик 1 |
1 |
||
| Стовпчик 2 |
-0,30202801 |
1 |
|
| Стовпчик 3 |
0,279578475 |
-0,25820294 |
1 |
3. Регресійний аналіз
За допомогою команди Регресія Аналізу даних Excel (рис.2) проведемо регресійний аналіз.
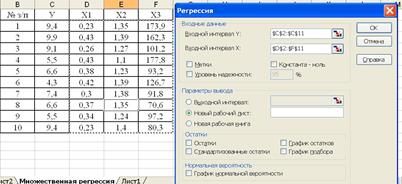
Рис.2. Процес проведення регресійного аналізу.
Виходячи з даних таблиці 2, маємо наступні висновки:
1. Коефіцієнт множинної детермінації показує, що приблизно 50% зміни змінної У залежить від змін змінних Х. Це свідчить про доволі щільний зв’язок, враховуючи як мінімум три фактори впливу (три змінні).
2. Рівень спостережень (10) дозволяє судити про достатній рівень для оцінки множинної регресії.
3. F більша за значимість F. Це означає, що з 5% -м ризиком помилки можна стверджувати, що з імовірністю, більшою за 95%, можна стверджувати, що між змінними Х1, Х2 та Х3 існує лінійна залежність.
4. Мультиколлінеарність – це становище, за якого одна чи більше незалежних змінних, що входять до рівняння регресії, є точними лінійними функціями від однієї чи більше інших незалежних змінних того самого рівняння. Наявність мультиколлінеарності визначає коефіцієнт детермінації. Його значення, що свідчить про залежність незалежних змінних одна від одної. Отже, спостерігаємо наявність мультиколлінеарності.
Виходячи з результатів даного аналізу маємо наступне рівняння регресії (найкраще):
![]()
Таблиця 2
Результати регресійного аналізу Excel
| ВЫВОД ИТОГОВ |
||||||||
| Регрессионная статистика |
||||||||
| Множественный R |
0,711739446 |
|||||||
| R-квадрат |
0,506573039 |
|||||||
| Нормированный R-квадрат |
0,259859559 |
|||||||
| Стандартная ошибка |
1,70239339 |
|||||||
| Наблюдения |
10 |
|||||||
| Дисперсионный анализ |
||||||||
| df |
SS |
MS |
F |
Значимость F |
||||
| Регрессия |
3 |
17,85214 |
5,950713 |
2,053285 |
0, 208003285 |
|||
| Остаток |
6 |
17,38886 |
2,898143 |
|||||
| Итого |
9 |
35,241 |
||||||
| Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
|
| Y-пересечение |
1,705455824 |
9,48843 |
0,179741 |
0,863273 |
-21,51189547 |
24,92280712 |
-21,51189547 |
24,92280712 |
| Переменная X 1 |
-14,451294 |
7,646333 |
-1,88996 |
0,107657 |
-33,16119756 |
4,258609463 |
-33,16119756 |
4,258609463 |
| Переменная X 2 |
6,506205971 |
6, 202293 |
1,049 |
0,334583 |
-8,670259371 |
21,68267131 |
-8,670259371 |
21,68267131 |
| Переменная X 3 |
0,017365132 |
0,015039 |
1,154705 |
0,292119 |
-0,019432971 |
0,054163235 |
-0,019432971 |
0,054163235 |
Додаток 1
Таблиця проміжних розрахунків до Завдання 1.
| i |
x |
y |
х2 |
х*y |
ŷ |
у-уср |
(у-уср) 2 |
(ŷ - уср) 2 |
(у - ŷ) 2 |
х-х |
(х-х) 2 |
(х-х) (у-у) |
| 1 |
0,15 |
1,35 |
0,0225 |
0, 2025 |
1,3071 |
0,0400 |
0,0016 |
0,00000861 |
0,0018 |
-0,2550 |
0,0650 |
-0,0102 |
| 2 |
0,34 |
1,39 |
0,1156 |
0,4726 |
1,3093 |
0,0800 |
0,0064 |
0,00000056 |
0,0065 |
-0,0650 |
0,0042 |
-0,0052 |
| 3 |
0,09 |
1,27 |
0,0081 |
0,1143 |
1,3064 |
-0,0400 |
0,0016 |
0,00001314 |
0,0013 |
-0,3150 |
0,0992 |
0,0126 |
| 4 |
0,05 |
1,1 |
0,0025 |
0,055 |
1,3059 |
-0,2100 |
0,0441 |
0,00001669 |
0,0424 |
-0,3550 |
0,1260 |
0,0746 |
| 5 |
0,48 |
1,23 |
0,2304 |
0,5904 |
1,3109 |
-0,0800 |
0,0064 |
0,00000074 |
0,0065 |
0,0750 |
0,0056 |
-0,0060 |
| 6 |
0,41 |
1,39 |
0,1681 |
0,5699 |
1,3101 |
0,0800 |
0,0064 |
0,00000000 |
0,0064 |
0,0050 |
0,0000 |
0,0004 |
| 7 |
0,62 |
1,38 |
0,3844 |
0,8556 |
1,3125 |
0,0700 |
0,0049 |
0,00000612 |
0,0046 |
0,2150 |
0,0462 |
0,0151 |
| 8 |
0,5 |
1,35 |
0,25 |
0,675 |
1,3111 |
0,0400 |
0,0016 |
0,00000120 |
0,0015 |
0,0950 |
0,0090 |
0,0038 |
| 9 |
1,2 |
1,24 |
1,44 |
1,488 |
1,3191 |
-0,0700 |
0,0049 |
0,00008369 |
0,0063 |
0,7950 |
0,6320 |
-0,0557 |
| 10 |
0,21 |
1,4 |
0,0441 |
0,294 |
1,3078 |
0,0900 |
0,0081 |
0,00000504 |
0,0085 |
-0, 1950 |
0,0380 |
-0,0176 |
| Σ |
4,05 |
13,1 |
2,6657 |
5,3173 |
0,0860 |
0,00013578 |
0,0859 |
1,0255 |
0,0118 |
|||
| Σ/і |
0,4050 |
1,3100 |
0,2666 |
0,5317 |
0,0086 |
0,00001358 |
0,0086 |
0,1025 |
0,0012 |
Похожие работы
-
Класична лінійна регресія
ЛАБОРАТОРНА РОБОТА №1 ТЕМА: КЛАСИЧНА ЛІНІЙНА РЕГРЕСІЯ Мета: Дослідити метод побудови загальної лінійної регресії та провести аналіз її основних характеристик
-
Економіко-математичні методи і алгоритми
Завдання 1 У наведеній далі задачі виконати такі дії: 1.1. записати математичні моделі прямої та двоїстої задач; 1.2. симплекс-методом визначити оптимальні плани прямої та двоїстої задач, подати їх економічний аналіз;
-
Теорія ймовірностей та математична статистика
Міністерство освіти і науки України Донбаський державний технічний університет Кафедра Вищої Математики КОНТРОЛЬНА РОБОТА По дисципліні “Теорія ймовірностей та математична статистика”
-
Двокроковий метод найменших квадратів
Двокроковий метод найменших квадратів Нехай маємо таку модель: функція доходу: функція пропозиції грошей: – доход; – запас грошей; – інвестиційні витрати;
-
Розвязування економетричних задач
Лабораторна робота № 1 Тема. Застосування електронних таблиць EXCEL та пакетів прикладних програм для розв’язування економетричних задач Мета роботи: ознайомитися з порядком застосування електоронних таблиць та пакетів прикладних програм у сатистичних та економетричних розрахунках.
-
Побудова споживчої функції. Оцінка параметрів системи економетричних рівнянь
Курсова робота з дисципліни “Економетрія ” Тема „Побудова споживчої функції дослідження мультиколінеарності між пояснюючими змінними. Оцінка параметрів системи економетричних рівнянь. Оцінка параметрів регресійної моделі з автокорельованими „
-
Обчислення матричних задач
МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ Бердичівський політехнічний коледж Контрольна робота з дисципліни “Числові методи” Виконав: студент групи Пзс-503 Лифар Сергій Олександрович
-
Розв'язання рівнянь методом оберненої матриці та методом Гауса
Запис системи рівнянь та їх розв'язання за допомогою методів оберненої матриці та Гауса. Поняття вектора-стовпця з невідомих та вільних членів. Пошук оберненої матриці до даної. Послідовне виключення невідомих за допомогою елементарних перетворень.
-
Методи та прийоми економічного аналізу
Лабораторна робота №1 Тема: «Методи та прийоми економічного аналізу» Мета роботи: Навчитися знаходити ступінь зв’язку між факторами за допомогою кореляційно-регресивного аналізу.
-
Елементи інформаційних технологій в математичному програмуванні
Завдання 1 Розв'язати графічним способом при умовах: Розв'язування Зобразимо розв’язок системи нерівностей та вектор F (1;2): Максимум функції досягається в точці А: