Referat.me / Математика / Методика регрессионного анализа

Название: Методика регрессионного анализа

Вид работы: контрольная работа

Размер файла: 414.37 Kb

Скачать файл: referat.me-215424.docx

Краткое описание работы: Министерство науки и образования Украины Национальный технический университет Украины "Киевский политехнический институт" Радиотехнический факультет

Методика регрессионного анализа

Министерство науки и образования Украины

Национальный технический университет Украины

"Киевский политехнический институт"

Радиотехнический факультет

Контрольная работа

По курсу: "Основы научных исследований"

Тема: "Методика регрессионного анализа"

Киев 2007

Нахождение коэффициентов регрессии модели полнофакторного эксперимента типа 2³

Факторный эксперимент связан с варьированием одновременно всех факторов и проверкой достоверности результатов математико-статистическими методами. Факторы в эксперименте можно варьировать на бесконечном множестве уровней. При планировании эксперимента, чтобы получить результаты эксперимента в виде удобных для анализа полиномов, достаточно изменять факторы на двух, трех или пяти уровнях. Проведение экспериментов с многоуровневыми факторами затруднительно, поэтому они находят ограниченное применение в практике инженерного эксперимента.

Таблица 1

Номер комбинации	Факторы				Произведения факторов				Параметры оптимизации (экспертная оценка)			Параметр оптимизации
	_	Ф	И	С	Произведения факторов				Параметры оптимизации (экспертная оценка)			Параметр оптимизации
	x0	x1	x2	x3	x1x2	x1x3	x2x3	x1x2x3	y1	y2	y3
1	1	-1	-1	-1	1	1	1	-1	0	0	0	0
2	1	1	-1	-1	-1	-1	1	1	31	28	47	35,3
3	1	-1	1	-1	-1	1	-1	1	12	9	10	10,3
4	1	1	1	-1	1	-1	-1	-1	60	52	64	58,7
5	1	-1	-1	1	1	-1	-1	1	1	3	2	2
6	1	1	-1	1	-1	1	-1	-1	54	59	50	54,3
7	1	-1	1	1	-1	-1	1	-1	41	41	40	40,7
8	1	1	1	1	1	1	1	1	91	92	90	91
Среднее значение								24,8

Модель для ПФЭ типа выглядит следующим образом:

Коэффициенты уравнения регрессии по методу наименьших квадратов в матричной форме определяем следующим образом [1, с. 53-55]:

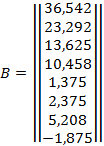
Выражение - квадратная симметричная матрица – называется матрицей системы нормальных уравнений, или информационной матрицей (матрицей Фишера); – ковариационная матрица, или матрица дисперсий ковариаций.

Ковариация показывает величину статистической взаимосвязи между эффектами модели x_i и x_j :

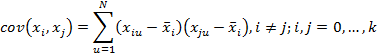
Также коэффициенты ковариаций можно определить из ковариационной матрицы:

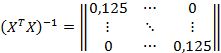
Из матрицы видно, что коэффициенты ковариаций каждого эффекта с каждым равны нулю, отсюда делаем вывод, что коэффициенты уравнения регрессии не коррелированны между собой.

Проверка многофакторных статистических моделей по основными критериям качества

Проверка на статистическую значимость получаемой математической модели [1, с. 93-94]

Проводиться проверка статистической гипотезы о силе влияния факторов плана эксперимента на фоне случайной изменчивости повторных опытов:

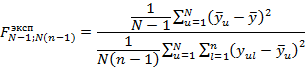
Где – среднее значения результатов опытов в u -той строке матрицы результатов; – среднее значение по всем результатам опытов; - результат в u -той строке l -го повторного опыта; (n – количество повторных опытов (2))

По таблице (приложение 3) определяем 3,73

Поскольку (53,935>3,73), то делаем положительный вывод о целесообразности получения математической модели.

Проверки предпосылок о свойствах случайных ошибок входящие в результаты экспериментов [1, с. 93]

При равномерном дублировании опытов n_u = n = const (в нашем случае n = 2). Проверка однородностиряда дисперсий производиться с использованием G -критерия Кохрена:

- вычисляется по формуле:

Число степеней свободы, которыми обладает каждая из дисперсий: n – 1 = 1;

Количество независимых оценок дисперсий: N = 8

По указанным индексам находим значение из таблицы "Критерий Кохрена" (приложение 1)

Так как то делаем вывод, что дисперсии однородны и могут быть усреднены:

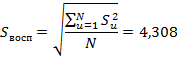
Проверка на адекватность полученной модели произвольным результатам экспериментов в пределах принятых изменений факторов [1, с. 94-95]

Проверка коэффициентов уравнения регрессии на статистическую значимость проводиться с помощью t -критерия:

Для значения α = 0,05, получим α/2 = 0,025 и значение t-критерия Стьюдента равно . Поскольку в матрице дисперсий-ковариаций не нулевые только диагональные элементы и равны между собой (), то все доверительные интервалы равны между собой:

Теперь проверим все коэффициенты на статистическую значимость исходя из условия: если – то коэффициент статистически значим, если – то коэффициент статистически не значим.

коэффициент	b₀	b₁	b₂	b₃	b₄	b₅	b₆	b₇
	36,542	23,292	13,625	10,458	1,375	2,375	5,208	1,875
Статистически значим	+	+	+	+	-	+	+	-

Таким образом мы получили, что коэффициенты b ₄ и b ₇ – статически не значимы, поэтому мы не будем вносить их в нашу модель. И окончательный вид модели будет таким:

Число = 6 – количество эффектов, которые вошли в структуру модели, то есть статистически значимые.

Значения откликов, полученных с помощью последней модели:

Отклик	y₁	y₂	y₃	y₄	y₅	y₆	y₇	y₈
	-3.25	38.584	13.584	55.418	2.5	53.834	40.166	91.5
	3.25	3.251	3.251	3.249	0.5	0.499	0.501	0.5

Проверка модели на адекватность производиться с использованием F -критерия Фишера:

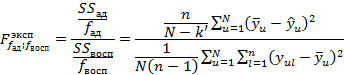
Где – числа степеней свободы для и :

Просчитаем экспериментальное значение:

По таблицам значения критерия Фишера (приложения 3) для q = 0,05 находим:

Так как выполняется условие значит модель адекватна.

Так как у нас , то нет необходимости определять значимость обратного отношения дисперсий.

Проверка на информативность [1, с. 97-99]

Коэффициент множественной корреляции R определяется по формуле:

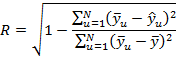
Посчитанное значение R = 0,997 которое очень близко к единице.

Гипотезу о значимости множественного коэффициента корреляции проверяют по F -критерию:

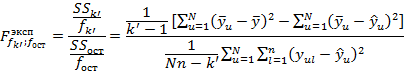
Где – суммы квадратов отклонений – связанная с коэффициентом модели и остаточная; – числа степеней свободы для и .

В нашем случае:

По таблицам значения критерия Фишера для q = 0,05 находим:

Поскольку , то гипотеза о статистической незначимости R не принимается – это значит, что коэффициент множественной корреляции R является статистически значимым.

Проверка на устойчивость коэффициентов математической модели к случайным составляющим в исходной информации [1, с. 99-101]

Коэффициенты математической модели должны быть устойчивы к малым случайным изменениям в исходных данных, полученных в процессе эксперимента. Для количественно показателя устойчивости коэффициентов математической модели будем использовать меру обусловленности матрицы по Нейману-Голдстейну.

Для определения меры обусловленности по Нейману-Голдстейну P необходимо найти собственные числа для матрицы Фишера , решая уравнение:

Где – собственные числа для информационной матрицы Фишера

Поскольку коэффициенты b ₄ и b ₇ статистически незначимы, тога соответствующие столбцы матрицы X отбрасываются и размер матрицы становится , размер обратной матрицы - , а размер матрицы Фишера - :

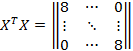
Так как все эффекты в матрице Фишера ортогональны друг другу и нормированы, то:

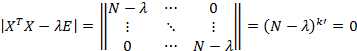
Находят – максимальное и минимальное собственное число для информационной матрицы Фишера :

Мера обусловленности по Нейману-Голдстейну:

Другая мера обусловленности матрицы обозначается латинским сокращением cond :

- обозначение нормы матрицы. При этом предполагается, что матрица невырождена.

Известны несколько видов норм для матрицы А . Каждой из векторных норм соответствует своя подчиненная норма матрицы. Будем использовать следующую форму:

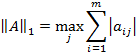
что означает выбор по всем столбцам j максимальной суммы абсолютных значений элементов по строкам i (m – число строк матрицы А ).

Так как все эффекты в расширенной матрице X ортогональны друг другу, то:

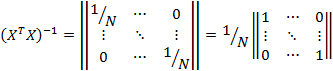
Для матрицы каждая по столбцам . Для матрицы каждая по столбцам .

Число обусловленности в этом случае будет:

Что подтверждает результат, полученный предыдущим методом.

Проверка фактической эффективности извлечения полезной информации из исходных данных [1, с. 101-102]

Косвенным показателем эффективности может быть число обусловленности cond для полученной модели. Так как значит эффективность можно считать хорошей.

Проверка правильности описания полученной математической модели по всей области моделирования [1, с. 102]

Полученную математическую модель желательно проверить по контрольной выборке. С использованием ПС ПРИАМ можно построить трехмерное изображение поверхности отклика, и проанализировать полученную поверхность, сравнивая минимальные и максимальные расчетные значения с допустимыми физическими значениями отклика. Возможен также поиск минимума и максимума по модели с использованием ЛПτ равномерно распределенных последовательностей и сравнения с физически возможными значениями отклика.

Оценка семантичности по полученным коэффициентам математической модели [1, с. 102-103]

Семантичность достигается, если эффекты статистической модели ортогональны друг другу, нормированы и план эксперимента равномерный. Выбор структуры модели должен быть проведен с использованием алгоритма RASTA3 и ПС ПРИАМ.

В нашем случае все эффекты полученной модели ортогональны друг другу и нормированы, план эксперимента мы выбрали равномерный, следовательно семантичность достигается.

Проверка свойств остатков [1, с. 103, 364-366]

Анализ основных графиков остатков

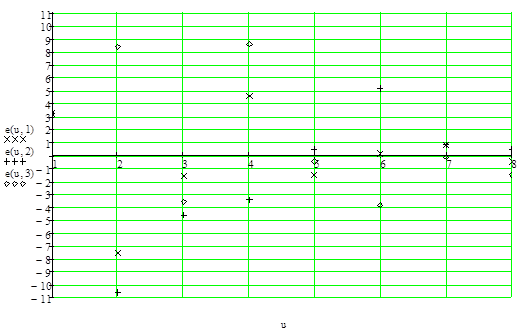
Общая оценка свойств полученной математической модели и возможностей ее использования для достижения поставленной цени

Из вышеприведенных расчетов и проверок можно сделать вывод, что данная математическая модель является адекватной для ее использования в поставленных задачах.

Литература

1. Рядченко С.Г. Устойчивые методы оценивания статистических моделей. Монография. – К.: ПП "Санспарель", 2005. – 504 с.

2. Большов Л.Н., Смирнов Н.В. Таблицы математической статистики

Приложения

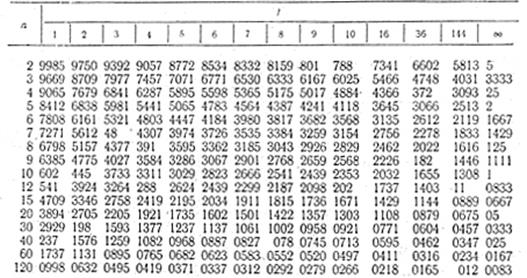
1. Значение критерия Кохрена G_1- _q для q = 0,05. Все значения G_1- _q меньше единицы, поэтому в таблице приведены лишь знаки, следующие после запятой.

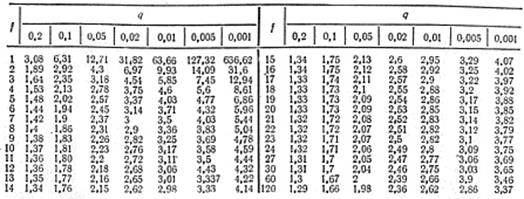
2. Значения критерия Стьюдента (t - критерия)

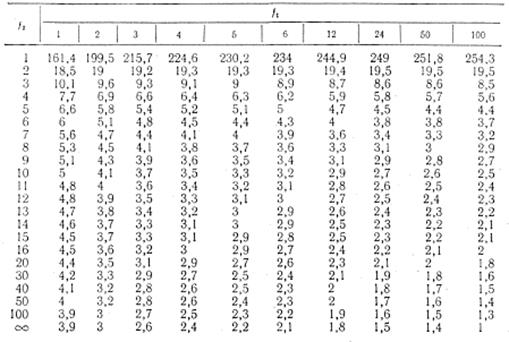
3. Значения критерия Фишера F_1- _q для q = 0,05