Название: Математика
Вид работы: контрольная работа
Рубрика: Математика
Размер файла: 20.85 Kb
Скачать файл: referat.me-215678.docx
Краткое описание работы: Определить объемы выпуска каждого вида продукции, обеспечивающие предприятию получение наибольшей прибыли при реализации продукции. Оптимальный план перевозки грузов от поставщиков к потребителям, обеспечивающий минимальные затраты. Система неравенств.
Математика
ЗАДАЧА №1
Предприятие выпускает четыре вида продукции П1, П2, П3, П4, при ограниченных запасах сырья С1, С2, С3, используемых для производства продукции. Известна прибыль, получаемая от реализации каждого вида продукции. Требуется определить объемы выпуска каждого вида продукции, которые обеспечат предприятию получение наибольшей прибыли при реализации продукции.
Расход сырья на производство единицы продукции, запасы сырья и прибыль, получаемая от реализации единицы продукции, приведены в таблице.
| Виды сырья | Расход сырья | Запасы сырья | |||
| П1 | П2 | П3 | П4 | ||
| С1 | 2 | 0 | 1 | 2 | 800 |
| С2 | 1 | 2 | 0 | 3 | 900 |
| С3 | 2 | 1 | 2 | 3 | 1500 |
| Прибыль | 8 | 6 | 7 | 9 | --- |
Решение
Пусть Х1, Х2, Х3, Х4 – количество единиц выпускаемой продукции П1, П2, П3, П4 соответственно.
Тогда функция прибыли примет вид:
F(х)=8Х1+6Х2+7Х3+9Х4→max
![]() Запишем ограничения по расходу сырья в виде системы неравенств:
Запишем ограничения по расходу сырья в виде системы неравенств:
2Х1+Х3+2Х4≤800
Х1+2Х2+3Х4≤900
2Х1+Х2+2Х3+3Х4≤1500
Х1,2,3≥0
Перейдем от неравенств к равенствам:
![]() 2Х1+Х3+2Х4+Х5=800
2Х1+Х3+2Х4+Х5=800
Х1+2Х2+3Х4+Х6=900
2Х1+Х2+2Х3+3Х4+Х7=1500
Решение будем вести в форме симплекс-таблиц.
| № п/п | Х баз | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Вi | Вi/ аiк |
| 1 | Х5 | 2 | 0 | 1 | 2 | 1 | 0 | 0 | 800 | 800 |
| 2 | Х6 | 1 | 2 | 0 | 3 | 0 | 1 | 0 | 900 | - |
| 3 | Х7 | 2 | 1 | 2 | 3 | 0 | 0 | 1 | 1500 | 750 |
| «0» | F(х) | -8 | -6 | -7 | -9 | 0 | 0 | 0 | 0 | |
| 1 | Х5 | 1 | -0,5 | 0 | 0,5 | 1 | 0 | -0,5 | 50 | -100 |
| 2 | Х6 | 1 | 2 | 0 | 3 | 0 | 1 | 0 | 900 | 450 |
| 3 | Х3 | 1 | 0,5 | 1 | 1,5 | 0 | 0 | 0,5 | 750 | 1500 |
| «0» | F(х) | -1 | -2,5 | 0 | 1,5 | 0 | 0 | 3,5 | 5250 | |
| 1 | Х5 | 1,25 | 0 | 0 | 1,25 | 1 | 0,25 | -0,5 | 275 | |
| 2 | Х2 | 0,5 | 1 | 0 | 1,5 | 0 | 0,5 | 0 | 450 | |
| 3 | Х3 | 0,75 | 0 | 1 | 0,75 | 0 | -0,25 | 0,5 | 525 | |
| «0» | F(х) | 0,25 | 0 | 0 | 5,25 | 0 | 1,25 | 3,5 | 6375 |
Как видим, в последней строке все числа положительны, следовательно полученный план является оптимальным.
Для получения максимальной прибыли необходимо выпускать 450 ед. продукции П2 и 525 ед. продукции П3. Максимальная прибыль в этом случае составит 6375 ден. ед.
ЗАДАЧА № 2
Имеется 4 поставщика и 4 потребителя. Известны тарифы на перевозку единицы груза от каждого поставщика к каждому потребителю. Найти оптимальный план перевозки грузов от поставщиков к потребителям, обеспечивающий минимальные затраты.
1130 1220 |
Потребители | ||||
| 320 | 280 | 210 | 320 | ||
| Поставщики | 420 | 5 | 8 | 1 | 5 |
| 180 | 2 | 6 | 5 | 7 | |
| 350 | 7 | 4 | 9 | 8 | |
| 270 | 6 | 2 | 7 | 9 | |
Так как количество груза у поставщиков (1220) превышает требуемое потребителями количество груза (1130) на 1220 – 1130=90 ед., то введем фиктивного потребителя с количеством груза 90 ед. и нулевыми тарифами на перевозку. Первоначальный опорный план составим методом двойного предпочтения, далее будем его улучшать методом потенциалов.В правом верхнем углу указаны тарифы на перевозку, в левом верхнем углу – сумма потенциалов, внизу по центру – количество перевозимого груза.
| 320 | 280 | 210 | 320 | 90 | Ui | |
| 420 | 4 5 |
1 8 |
1 1 210 |
5 5 210 |
-3 0 |
0 |
| 180 | 2 2 180 |
-1 6 |
-1 5 |
3 7 |
-5 0 |
-2 |
| 350 | 7 7 140 |
4 4 10 |
4 9 |
8 8 110 |
0 0 90 |
3 |
| 270 | 5 6 |
2 2 270 |
2 7 |
6 9 |
-2 0 |
1 |
| Vj | 4 | 1 | 1 | 5 | -3 |
В полученном плане перевозок для всех ячеек сумма потенциалов (Ui+ Vj) не превышает тарифы. Следовательно этот план перевозок является оптимальным и его нельзя улучшить.
Минимальные затраты на перевозку составят:
210*1+210*5+180*2+140*7+10*4+110*8+90*0+270*2=4 060 ден. ед.
ЗАДАЧА №3
Требуется расставить 5 рабочих по технологической цепочке так, чтобы время выполнения всего цикла операций было минимальным. Время, затрачиваемое каждым рабочим при выполнении любой операции приведено в таблице.
| 1-я | 2-я | 3-я | 4-я | 5-я | |
| 1-й | 7 | 8 | 6 | 9 | 7 |
| 2-й | 8 | 7 | 9 | 8 | 7 |
| 3-й | 9 | 8 | 6 | 7 | 5 |
| 4-й | 7 | 6 | 8 | 9 | 8 |
| 5-й | 8 | 9 | 5 | 4 | 9 |
Решение
| 1-я | 2-я | 3-я | 4-я | 5-я | |
| 1-й | 7 | 8 | 6 | 9 | 7 |
| 2-й | 8 | 7 | 9 | 8 | 7 |
| 3-й | 9 | 8 | 6 | 7 | 5 |
| 4-й | 7 | 6 | 8 | 9 | 8 |
| 5-й | 8 | 9 | 5 | 4 | 9 |
| qimin | 7 | 6 | 5 | 4 | 5 |
Zmin=4
| 1-я | 2-я | 3-я | 4-я | ||
| 1-й | 3 | 4 | 2 | 5 | 3 |
| 2-й | 4 | 3 | 5 | 4 | 3 |
| 3-й | 5 | 4 | 2 | 3 | 1 |
| 4-й | 3 | 2 | 4 | 5 | 4 |
| 5-й | 5 | 1 | 0 | 5 | |
| qimin | 3 | 2 | 2 | 1 |
![]() Zmin=1
Zmin=1
| 1-я | 2-я | 3-я | 4-я | 5-я | |
| 1-й | 2 | 3 | 1 | 5 | 2 |
| 2-й | 3 | 2 | 4 | 4 | 2 |
| 3-й | 3 | 1 | 3 | 0 | |
| 4-й | 2 | 1 | 3 | 5 | 3 |
| 5-й | 5 | 1 | 0 | 5 | |
| qimin | 2 | 1 | 1 |
Zmin=1
| 1-я | |||||
| 1-й | 2 | 0 | 5 | 2 | |
| 2-й | 2 | 1 | 3 | 4 | 2 |
| 3-й | 3 | 1 | 3 | 0 | |
| 4-й | 0 | 2 | 5 | 3 | |
| 5-й | 5 | 1 | 0 | 5 | |
| qimin | 2 | 1 | 1 |
В конечном виде:
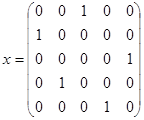
или:
| 1-я | 2-я | 3-я | 4-я | 5-я | |
| 1-й | 7 | 8 | 6 | 9 | 7 |
| 2-й | 8 | 7 | 9 | 8 | 7 |
| 3-й | 9 | 8 | 6 | 7 | 5 |
| 4-й | 7 | 6 | 8 | 9 | 8 |
| 5-й | 8 | 9 | 5 | 4 | 9 |
Время выполнения цикла: 6+8+5+6+4=29 ед. времени.
Похожие работы
-
Анализ экономических задач оптимизации
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТОГОВО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ
-
Решение задачи линейного программирования симплексным методом
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение Высшего профессионального образования «Волгоградский государственный технический университет»
-
Типовой расчет по ЭМММ
Типовой расчет Решение задач по дисциплине ЭМММ Вариант №23 Выполнил: Проверил: Екатеринбург 2009 Математическая модель ЗЛП Мат. модель ЗЛП называется стандартной, если система ограничений представлена в виде неравенств, а функция минимизируется или максимизируется
-
Математические программирование
ЛАБОРАТОРНАЯ РАБОТА №2 по мат.программированию «Графический и симплексный методы решения ОЗЛП» Для изготовления 2-х различных изделий А и В используется 3 вида сырья. На производство единицы изделия А требуется затратить сырья 1-го вида а1 кг, сырья 2-го вида – а2 кг, сырья 3-го вида – а3 кг. На производство единицы изделия В требуется затратить сырья 1-го вида в1 кг, сырья 2-го вида – в2 кг, сырья 3-го вида – в3 кг.
-
Математическое моделирование
Математическое моделирование экономических параметров: определение вида и параметров функций спроса, затрат и производственной функции выпуска.
-
Курсовая работа по прикладной математике
Министерство общего и профессионального образования Российской Федерации ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ ИНСТИТУТ ЗАОЧНОГО ОБУЧЕНИЯ Контрольная работа
-
Системы уравнений межотраслевого баланса
Выработать у студентов навыки построения математических моделей межотраслевого баланса в статистических случаях и оптимизации моделей в рамках межотраслевого баланса. Научиться делать выводы в рамках построения моделей.
-
Применение линейного программирования для решения задач оптимизации
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ Филиал в г. Брянске Контрольная РАБОТА по дисциплине ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И ПРИКЛАДНЫЕ МОДЕЛИ
-
Транспортная задача и задача об использовании сырья
1. Решить задачу об использовании сырья геометрическим способом и симплекс методом, дать экономическую интерпретацию. Геометрический способ. Пусть
-
Сетевые модели
Пути наиболее адекватной газификации села, разработка кратчайшего пути прокладывания газопровода. Оптимизация маршрута доставки груза. Определение минимального срока работ по новому направлению предприятия, срок окупаемости и возврата кредита в банк.