Название: Транспортная задача и задача об использовании сырья

Вид работы: реферат

Рубрика: Математика

Размер файла: 98.43 Kb

Скачать файл: referat.me-216174.docx

Краткое описание работы: 1. Решить задачу об использовании сырья геометрическим способом и симплекс методом, дать экономическую интерпретацию. Геометрический способ. Пусть

Транспортная задача и задача об использовании сырья

Транспортная задача и задача об использовании сырья

1. Решить задачу об использовании сырья геометрическим способом и симплекс методом, дать экономическую интерпретацию.

75	5	3
83	4	7
50	1	5
	4	5

Геометрический способ.

Пусть количество выпускаемой продукции первого вида, тогда количество выпускаемой продукции второго вида. Прибыль от реализации всей продукции составляет .

Цель задачи (максимализация прибыли) запишется в виде

Структура всех трёх ограничений одинакова

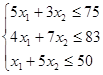
Перейдём из неравенств к уравнениям

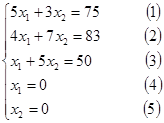
Построим прямые на плоскости

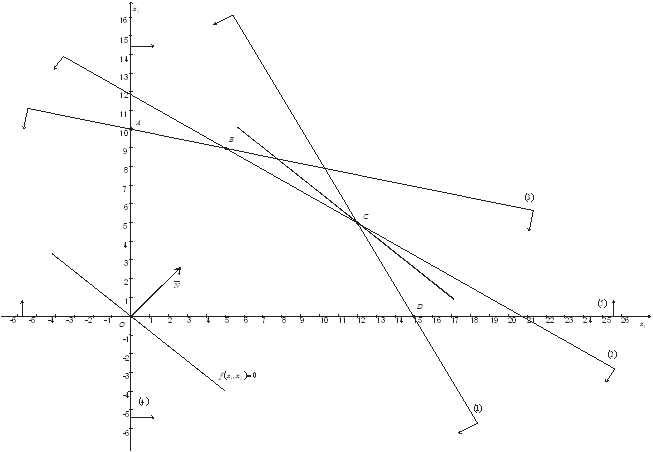
Многоугольник решений . Для нахождения максимума функции построим начальную прямую и вектор . Передвигая прямую вдоль вектора получим, что максимальное значение наша прямая принимает в точке точке пересечения прямых и .

.

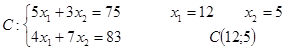
Симплекс метод.

Приведём систему неравенств к системе уравнений

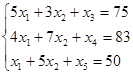
Целевая функция – функция прибыли

Составим симплекс таблицу:

- Первое ограничение запишем в первую строку

- Второе ограничение запишем во вторую строку

- Третье ограничение запишем в третью строку

Целевую функцию запишем в строку

Б	З
	75	5	3	1	0	0
	83	4	7	0	1	0
	50	1	5	0	0	1
	0			0	0	0

В строке есть отрицательные начальный план не оптимален. Найдём наименьший отрицательный элемент строки . Переменная будет включена в базис. Столбец переменной – ведущий. Подсчитаем симплексные отношения и найдём среди них минимальное третья строка ведущая, а элемент разрешающий. Следовательно переменная выйдет из базиса.

Проведём одну интеракцию метода замещения Жордано-Гаусса. Столбцы. Разрешающий элемент

равен поделим третью строку на 5, столбец сделаем единичным для этого третью строку умножим на и прибавим к первой строке, третью строку умножим на и сложим со второй строкой; третью строку сложим со строкой . Получим новую симплексную таблицу

Б	З
	45		0	1	0
	13		0	0	1
	10		1	0	0
	50		0	0	0	1

В строке есть отрицательные план не оптимальный. Рассчитаем симплексные отношения и найдём среди них минимальное вторая строка ведущая разрешающий

Следовательно, переменная выйдёт из базиса. Так как разрешающий элемент , поделим строку, соответствующую переменной на . Элементы столбца, соответствующего переменной отличны от элемента сделаем нулевыми, для этого вторую строку умножим на и прибавим к первой; вторую строку умножим на и прибавим к третьей; вторую строку умножим на и прибавим к строке . Получим новую симплексную таблицу

Б	З
	23	0	0	1
	5	1	0	0
	9	0	1	0
	65	0	0	0

В строке есть отрицательный элемент – пересчитываем таблицу. Рассчитываем симплексные отношения и найдём среди них минимальные первая строка ведущая разрешающий элемент переменная выйдет из базиса. Сделаем элемент единичным, для этого поделим первую строку на . Столбец, соответствующий переменной сделаем единичным для этого первую строку умножим на и прибавим ко второй строке. Первую строку умножим на и прибавим к третьей. Первую строку умножим на и прибавим к строке . Получим новую симплексную таблицу.

Б	З
	13	0	0			1
	12	1	0			0
	5	0	1			0
	73	0	0			0

Так как в строке все элементы неотрицательны, то найден оптимальный план

Оптимальный план найденный геометрическим способом и симплексным методом совпадают. Предприятию необходимо выпускать 12 единиц продукции первого вида и 5 единиц продукции второго вида. В этом случае предприятие получит прибыль денежных единиц.

2. Решить транспортную задачу распределительным методом, оценивая свободные клетки по методу потенциалов.

	60	50	85	75
65	8	10	6	5 65
80	4 30	3 50	5	9
35	11 25	4	4	8 10
90	5 5	5	3 85	6

Проверим необходимое и достаточное условие разрешимости задачи

Потребность в грузе равна запасам груза задача закрытая, следовательно, имеет единственное решение.

Используя метод наименьшей стоимости заполним таблицу.

Среди тарифов наилучшим является и . Направим например,

в клетку

в клетку

в клетку

в клетку

в клетку

в клетку

в клетку

Запасы поставщиков исчерпаны, запросы потребителей удовлетворены полностью. В результате получили первый опорный план. Подсчитаем число занятых клеток таблицы их 7, а должно быть опорный план не вырожденный.

Определим значение целевой функции первого опорного плана

Проверим оптимальность плана.

Найдём потенциалы и по занятым клеткам таблицы

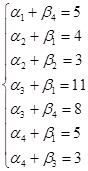
Пусть , тогда:

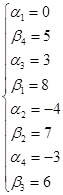
Подсчитаем оценки свободных клеток

Первый опорный план не является оптимальным так как .

Переходим к его улучшению. Для клетки строим цикл перераспределения

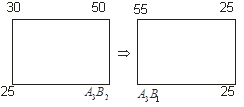
В результате получили новый опорный план

	60	50	85	75
65	8	10	6	5 65
80	4 55	3 25	5	9
35	11	4 25	4	8 10
90	5 5	5	3 85	6

Определим значение целевой функции

Проверим оптимальность плана

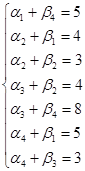
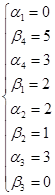
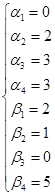
Подсчитаем оценки свободных клеток

План близок к оптимальному.

При дальнейшем перераспределении груза, задача входит в циклическую фазу, план не улучшается. Таким образом, полученное решение является наиболее оптимальным для нашей задачи