Название: Решение произвольных систем линейных уравнений

Вид работы: реферат

Рубрика: Математика

Размер файла: 75.38 Kb

Скачать файл: referat.me-215701.docx

Краткое описание работы: Рассмотрение систем линейных алгебраических уравнений общего вида. Сущность теорем и их доказательство. Особенность трапецеидальной матрицы. Решение однородных и неоднородных линейных алгебраических уравнений, их отличия и применение метода Гаусса.

Решение произвольных систем линейных уравнений

Дисциплина: Высшая математика

Тема: Решение произвольных систем линейных уравнений

1. Решение произвольных систем линейных алгебраических уравнений

Выше рассмотрены решения квадратных невырожденных систем линейных алгебраических уравнений матричным методом и методом Крамера. Однако они не пригодны в тех случаях, когда квадратная система уравнений вырождена или когда система вообще не является квадратной.

В связи с этим перейдем к рассмотрению систем линейных алгебраических уравнений общего вида, когда :

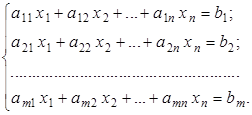
В данном случае матрица системы является прямоугольной, у нее нет определителя, и метод Крамера для решения системы не применим. Поэтому, прежде чем решать данную систему, рассмотрим две теоремы.

Теорема 1.1. Если ранг матрицы совместной системы линейных алгебраических уравнений равен числу неизвестных, то система имеет единственное решение .

Доказательство. Если ранг матрицы системы равен , то есть числу неизвестных, то строк у матрицы должно быть тоже . Следовательно, . Итак, по условию . Но тогда любая, не входящая в базисный минор, строка расширенной матрицы является линейной комбинацией базисных строк и может быть обращена в ноль. То же самое происходит и с уравнением, соответствующим этой строке. Значит, исходная система эквивалентна уравнениям с коэффициентами из базисного минора. Остальные уравнений из системы можно убрать, так как они является линейной комбинацией оставшихся. Получаем квадратную невырожденную систему линейных алгебраических уравнений с неизвестными, которая согласно правилу Крамера имеет единственное решение, что и требовалось доказать.

Теорема 1.2. Если ранг матрицы совместной системы линейных алгебраических уравнений меньше числа неизвестных, то система имеет бесконечное множество решений .

Доказательство. По условию система совместна и . Будем считать, что базисный минор расположен в левом верхнем углу расширенной матрицы системы . Если это не так, то, переставляя строки и столбцы матрицы, можно получить нужный результат.

Минор будет иметь вид:

.

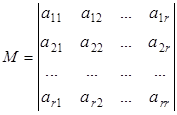Так как любая строка матрицы , не вошедшая в базисный минор, является линейной комбинацией базисных, то ее можно обратить в ноль. Тогда, по аналогии с теоремой 1.1, из исходной системы можно убрать те уравнения, коэффициенты которых не попали в базисный минор. Следовательно, в ней останется линейных алгебраических уравнений и исходную систему можно записать в виде:

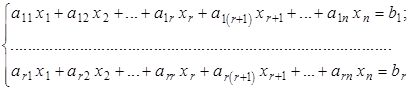
или

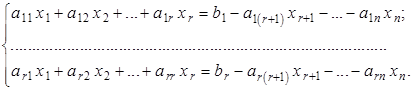
Придавая неизвестным произвольные значения , получаем систему из уравнений с неизвестными:

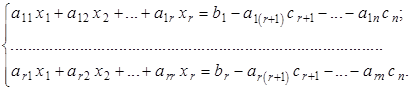
Данная система является квадратной, ее определитель , поэтому с помощью метода Крамера находим единственное решение . Очевидно, задавая другие значения для , получим другие значения неизвестных .

Так как числа могут быть заданы произвольно, то число решений системы бесконечно. Какое-то одно решение будет иметь вид:

.

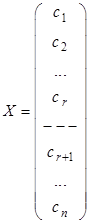Неизвестные, коэффициенты при которых входят в базисный минор, называются базисными. Остальные неизвестные называются свободными.

2. Система однородных линейных алгебраических уравнений

Важное место среди всех систем линейных алгебраических уравнений занимают однородные системы с произвольными и :

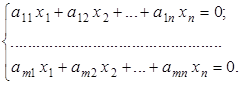
Данные системы всегда совместны, так как обязательно имеют решение вида , которое называется нулевым или тривиальным.

Если , то, согласно теореме 1.1, это решение будет единственным. В частности, в случае однородной невырожденной квадратной системы ее единственное решение будет тривиальным.

В случае, когда ранг матрицы системы меньше числа неизвестных, то решений, согласно теореме 1.2, будет бесконечное множество. Пусть в этом случае матрицы - столбцы , ,..., являются некоторыми решениями системы:

, ,..., .

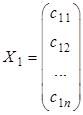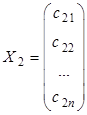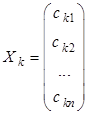Тогда выражение будет называться их линейной комбинацией. Очевидно, что можно ввести понятие линейно зависимой и линейно независимой системы этих решений. Необходимо иметь в виду, что линейная комбинация решений системы линейных алгебраических уравнений также будет ее решением. Действительно,

.

Теорема. Если ранг матрицы однородной системы линейных алгебраических уравнений меньше числа неизвестных, то есть , то существует линейно независимых решений системы , ,..., , а любые другие решения можно представить как их линейную комбинацию .

Доказательство. Пусть ранг основной матрицы системы . Тогда базисными неизвестными будут , а остальные неизвестных будут свободными. В этом случае произвольное решение системы можно записать в виде:

.

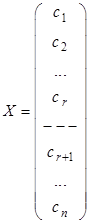Здесь – произвольные числа, а однозначно определяются из системы для выбранных .

Рассмотрим следующих решений системы:

, ,..., .

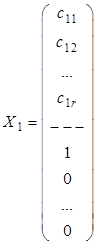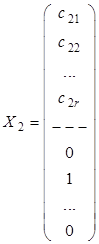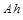По аналогии с результатом п. 6.3 все они линейно независимы, и произвольное решение системы можно представить в виде:

,

что и требовалось доказать.

Определение. Фундаментальной системой решений однородной системы линейных алгебраических уравнений называется совокупность всех ее линейно независимых решений .

Если в фундаментальной системе решений свободные неизвестные по очереди выражаются через единицу, в то время как остальные равны нулю, то такая фундаментальная система решений называется нормированной.

3. Метод Гаусса

Для решения произвольных однородных систем линейных алгебраических уравнений удобен метод Гаусса. Основан он на следующем.

При вычислении ранга расширенной матрицы системы линейных алгебраических уравнений с помощью элементарных преобразований ее приводят к трапецеидальному виду:

.

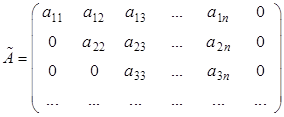Но если исходная матрица соответствует исходной системе уравнений, то трапецеидальная матрица будет соответствовать той же системе, но в измененном виде.

Особенность трапецеидальной матрицы заключается в том, что каждая ее последующая строка имеет на один ноль больше и, соответственно, на один коэффициент не равный нулю меньше. Строки, целиком состоящие из нулей, соответствуют исчезнувшим уравнениям. В последней строке будет один коэффициент не равный нулю и, значит, одна неизвестная в уравнении для определенной системы. В случае неопределенной системы в последнем уравнении будет одна базисная переменная и несколько свободных.

Находя эту базисную неизвестную из последнего уравнения, переходим затем к предпоследней строке и соответствующему ей уравнению и находим следующую базисную неизвестную. Эта операция повторяется до первой строки. После вычисления всех базисных неизвестных составляется нормированная фундаментальная система решений однородной системы линейных алгебраических уравнений.

4. Решение неоднородных систем линейных алгебраических уравнений

Выясним, чем отличается решение произвольной неоднородной системы алгебраических уравнений от решения однородной системы.

Определение. Однородная система линейных алгебраических уравнений называется соответствующей неоднородной системе, если коэффициенты при неизвестных у них одинаковые, а свободные члены неоднородной системы заменены нолями.

Рассмотрим произвольную совместную неоднородную систему линейных алгебраических уравнений:

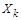
Пусть у нее в общем случае , то есть имеется бесконечное множество решений.

Теорема 4.1. Сумма любого решения неоднородной системы линейных алгебраических уравнений с любым решением соответствующей ей однородной системы является решением неоднородной системы .

Доказательство. Возьмем произвольное решение неоднородной системы

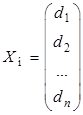
и произвольное решение соответствующей ей однородной системы

.

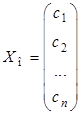Рассмотрим их сумму .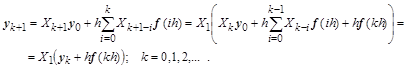

Если данная сумма является решением неоднородной системы, то она должна превратить в тождество любое ее уравнение:

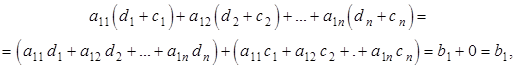
что и требовалось доказать.

Теорема 4.2. Разность любых двух решений неоднородной системы линейных алгебраических уравнений является решением соответствующей однородной системы .

Доказательство. Возьмем два произвольных решения неоднородной системы линейных алгебраических уравнени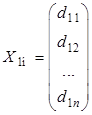й:

и .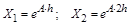

Составим их разность .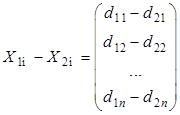

Подставим полученную разность в любое уравнение неоднородной системы:

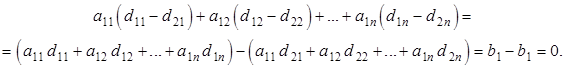
Так как левая часть уравнения обратилась в ноль, значит, является решением однородной системы, что и требовалось доказать.

Из теоремы 4.2 следует, что если , то . Иначе говоря, взяв какое-то одно решение неоднородной системы линейных алгебраических уравнений и прибавляя к нему разные решения соответствующей однородной системы , получим разные решения неоднородной системы, что подтверждается теоремой 4.1.

Следствие. Общее решение неоднородной системы линейных алгебраических уравнений равно сумме какого-то частного ее решения и общего решения соответствующей однородной системы .

Литература

1. Краснов М. Вся высшая математика т.1 изд.2. Едиториал УРСС, 2003. – 328с.

2. Мироненко Е. С. Высшая математика. М: Высшая школа, 2002. – 109с.

3. Черненко В. Д. Высшая математика в примерах и задачах. В трех томах. ПОЛИТЕХНИКА, 2003.

4. Шипачев В. С. Высшая математика изд.7 Изд-во: ВЫСШАЯ ШКОЛА, 2005. – 479с.