Referat.me
/ / Приложения определенного интеграла к решению некоторых задач механики и физики

Название: Приложения определенного интеграла к решению некоторых задач механики и физики

Вид работы: учебное пособие

Рубрика: Математика

Размер файла: 33.33 Kb

Скачать файл: referat.me-215805.docx

Краткое описание работы: Моменты и центры масс плоских кривых. Теорема Гульдена. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности.

Приложения определенного интеграла к решению некоторых задач механики и физики

Приложения определенного интеграла к решению некоторых задач механики и физики

1. Моменты и центры масс плоских кривых. Если дуга кривой задана уравнением y = f ( x ), a ≤ x ≤ b , и имеет плотность 1 ) = ( x ) , то статические моменты этой дуги Mx и My относительно коорди­натных осей Ox и O y равны

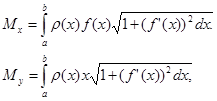
моменты инерции I Х и I у относительно тех же осей Ох и Оу вычис­ляются по формулам

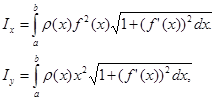
а координаты центра масс и — по формулам

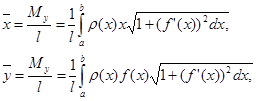
где l — масса дуги, т. е.

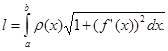
Пример 1. Найти статические моменты и моменты инерции относительно осей Ох

и Оу дуги цепной линии y = chx при 0≤ x ≤ 1.

1 ) Всюду в задачах, где плотность не указана, предполагается, что кривая однородна и =1.

◄ Имеем: Следовательно,

►

Пример 2. Найти координаты центра масс дуги окружности x=acost, y=asint, расположенной в первой четверти.

◄ Имеем:

Отсюда получаем:

►

В приложениях часто оказывается полезной следующая

Теорема Гульдена . Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости ду­ги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.

Пример 3. Найти координаты центра масс полуокружности

◄Вследствие симметрии . При вращении полуокружности вок­руг оси Ох получается сфера, площадь поверхности которой равна , а длина полуокружности равна па. По теореме Гульдена имеем

Отсюда , т.е. центр масс C имеет координаты C .

2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах 4—7.

Пример 4. Скорость прямолинейного движения тела выражает­ся формулой (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.

◄ Так как путь, пройденный телом со скоростью (t ) за отрезок времени [t1 ,t2 ], выражается интегралом

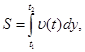
то имеем:

►

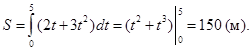Пример 5. Какую работу необходимо затратить для того, чтобы тело массы m поднять с поверхности Земли, радиус которой R, на высоту /i? Чему равна работа, если тело удаляется в беско­нечность?

<4| Работа переменной силы / (#), действующей вдоль оси Ох на от­резке [а, Ь], выражается интегралом

Похожие работы

  • Конус, и все что с ним связано

    КОНУС 1. Понятие конуса: тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Коническая поверхность называется боковой поверхностью конуса, а круг – основанием конуса

  • Вычисление интегралов

    Методика и основные этапы нахождения параметров: площади криволинейной трапеции и сектора, длины дуги кривой, объема тел, площади поверхности тел вращения, работы переменной силы. Порядок и механизм вычисления интегралов с помощью пакета MathCAD.

  • Формулы по математическому анализу

    Формулы дифференцирования Таблица основных интегралов Правила интегрирования Основные правила дифференцирования Пусть С—постоянная, u=u(x), v=v(x) – функции, имеющие

  • Кривые второго порядка эллипс, окружность, парабола, гипербола

    Федеральное агентство по образованию Российской Федерации Государственное образовательное учреждение высшего профессионального образования Южно-Уральский государственный университет.

  • Применение дифференциального и интегрального исчисления к решению физических и геометрических задач в MATLab

    История интегрального и дифференциального исчисления. Приложения определенного интеграла к решению некоторых задач механики и физики. Моменты и центры масс плоских кривых, теорема Гульдена. Дифференциальные уравнения. Примеры решения задач в MatLab.

  • Папп Александрийский. Теоремы Паппа-Гульдена

    В данной работе мы рассмотрим то немногое из биографии Паппа Алекасндрийского, что было нам приоткрыто из-за завесы веков и докажем одну из важнейших теорем интегрального исчисления – теорему Паппа-Гульдена.

  • Вычисление координат центра тяжести плоской фигуры

    Министерство общего и профессионального образования Российской федерации. Уральский Государственный Технический Университет - УПИ. Реферат ВЫЧИСЛЕНИЕ КООРДИНАТ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ.

  • Все о Конусе

    Муниципальное обще образовательное учреждение Средняя общеобразовательная школа №54 с углубленным изучение предметов социально-гуманитарного цикла центрального района города Новосибирска

  • Визначення та обчислення довжини дуги плоскої кривої в декартових та полярних координатах. Площа

    Пошукова робота на тему: Визначення та обчислення довжини дуги плоскої кривої в декартових та полярних координатах. Площа поверхні. План Довжина дуги кривої в декартових і полярних координатах

  • Техника интегрирования и приложения определенного интеграла

    Способы определения точного значения интеграла по формуле Ньютона-Лейбница и приближенного значения интеграла по формуле трапеций. Порядок нахождения координаты центра тяжести однородной плоской фигуры ограниченной кривой, особенности интегрирования.