Название: Техника интегрирования и приложения определенного интеграла
Вид работы: контрольная работа
Рубрика: Математика
Размер файла: 206.59 Kb
Скачать файл: referat.me-215242.docx
Краткое описание работы: Способы определения точного значения интеграла по формуле Ньютона-Лейбница и приближенного значения интеграла по формуле трапеций. Порядок нахождения координаты центра тяжести однородной плоской фигуры ограниченной кривой, особенности интегрирования.
Техника интегрирования и приложения определенного интеграла
Контрольная работа
по теме «Техника интегрирования и приложения определенного интеграла»
№ 314
Найти неопределенные интегралы:
![]()
![]()
![]()
№ 335
Найти определенный интеграл:
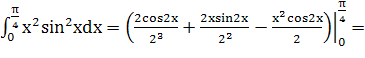
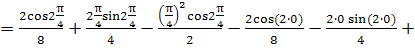
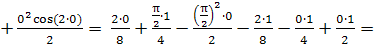
![]()
№ 356
Найти:
1. точное значение интеграла по формуле Ньютона-Лейбница;
2. приближенное значение интеграла по формуле трапеций, разбивая отрезок интегрирования на 8 равных частей и производя вычисления с округлением до 4 десятичных знаков;
3. относительную погрешность.
Решение:
1.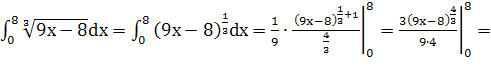
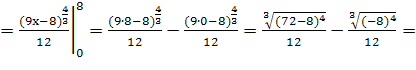
![]()
2.![]()
![]()
![]() , где
, где
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]()
№ 377
![]()
![]()
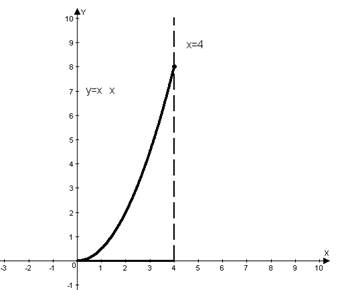
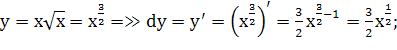
Пределы интегрирования по x от 0 до 4:
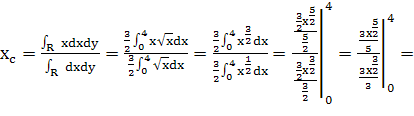
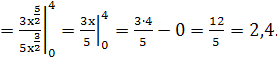
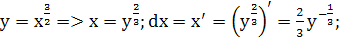
Пределы интегрирования по y от 0 до 8:
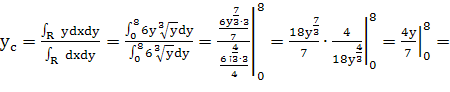
![]()
Координаты центра тяжести данной фигуры (2,4; 4,6).
№ 398
Вычислить несобственный интеграл или установить его расходимость:
![]()
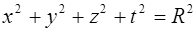
![]()
![]()

![]()
Несобственный интеграл вычислен и равен 1, следовательно он сходится.
№451
1. построить на плоскости хОу область интегрирования;
2. изменить порядок интегрирования и вычислить площадь области при заданном и измененном порядках интегрирования;
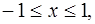
Решение:
1. Пределы внешнего интеграла по переменной х – числа 1 и 5 указывают на то, что область D ограничена слева прямой х = 1 и справа х = 5.
Пределы внутреннего интеграла по переменной у – указывают на то, что область D ограничена снизу параболой ![]() и сверху линией
и сверху линией ![]() .
.
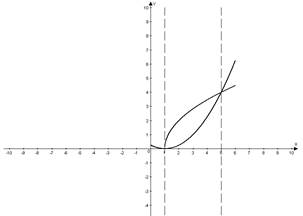
2. Чтобы изменить порядок интегрирования, установим пределы интегрирования для внешнего интеграла по переменной у. Как видно из рисунка, наименьшее значение которое принимает у в точке А(1;0) равно 0, а наибольшее значение в точке В(5; 4) равно 4. Т.О. новые пределы интегрирования: 0 – нижний, 4 – верхний.
Определим пределы для внутреннего интеграла по переменной х. Выразим х из уравнений:
![]()
![]()
![]()
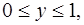
![]()
![]()
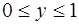
![]()
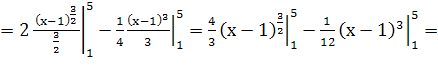
![]()
![]()
![]()
![]()
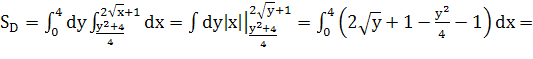
![]()
Похожие работы
-
Формулы по математическому анализу
Формулы дифференцирования Таблица основных интегралов Правила интегрирования Основные правила дифференцирования Пусть С—постоянная, u=u(x), v=v(x) – функции, имеющие
-
Вычисление определенного интеграла
Задача численного интегрирования функций. Вычисление приближенного значения определенного интеграла. Нахождение определенного интеграла методами прямоугольников, средних прямоугольников, трапеций. Погрешность формул и сравнение методов по точности.
-
Применение квадратурной формулы Чебышева для вычисления определенного интеграла
Данная задача заключается в решении определенного интеграла по квадратурной формуле Чебышева. Как известно, вычисление определенного интеграла сводится к вычислению площади криволинейной трапеции, ограниченной кривыми.
-
Приближенное вычисление определенных интегралов
Приближенное вычисление определенных интегралов; формула трапеций и формула парабол.
-
Приближенный метод решения интегралов. Метод прямоугольников (правых, средних, левых)
Лабораторная работа № 4. Приближенный метод решения интегралов. Метод прямоугольников (правых, средних, левых). Гребенникова Марина 12-А класс Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида
-
Вычисление координат центра тяжести плоской фигуры
Министерство общего и профессионального образования Российской федерации. Уральский Государственный Технический Университет - УПИ. Реферат ВЫЧИСЛЕНИЕ КООРДИНАТ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ.
-
Вычисление определенного интеграла методом трапеций и средних прямоугольников
БЕЛОРУССКИЙ АГРАРНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ КУРСОВАЯ РАБОТА на тему “вычисление определенного интеграла методами трапеций и средних прямоугольников”
-
Методы прямоугольников и трапеций
Методы прямоугольников и трапеций. Простейшим методом численного интегрирования является метод прямоугольников. Он непосредственно использует замену определенного интеграла интегральной суммой (3.20). В качестве точек
-
Численное интегрирование функций
Характеристика методов численного интегрирования, квадратурные формулы, автоматический выбор шага интегрирования. Сравнительный анализ численных методов интегрирования средствами MathCAD, а также с использованием алгоритмических языков программирования.
-
Приложения определенного интеграла к решению некоторых задач механики и физики
Моменты и центры масс плоских кривых. Теорема Гульдена. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности.