Название: Нахождение площади живого сечения траншеи

Вид работы: реферат

Рубрика: Математика

Размер файла: 34.24 Kb

Скачать файл: referat.me-216230.docx

Краткое описание работы: 1. Формулировка проблемы. Сечение траншеи имеет форму близкую к сегменту параболы, ширина траншеи на её поверхности l метров наибольшая глубина H метров . найти площадь «живого сечения» траншеи , если она полностью заполнена водой.

Нахождение площади живого сечения траншеи

1. Формулировка проблемы.

Сечение траншеи имеет форму близкую к сегменту параболы, ширина траншеи на её поверхности l метров наибольшая глубина H метров . найти площадь «живого сечения» траншеи , если она полностью заполнена водой.

Дано:

l=1,5 Найти: S живого сечения траншеи

Н=2,25

2. Пояснение к решению.

· Прибавляя постоянную к первообразной какой-либо функции, вновь получают первообразную той же функции. Следовательно, имея одну первообразную F(x) функции f (x), получают общее выражение всех первообразных этой функции в виде F(x) + С. (Постоянная C называется произвольной постоянной). Это общее выражение первообразных называют неопределённым интегралом.

· Приращение первообразных функций F(x)+C при переходе аргумента x от значения x=a к значению x=b , равное разности F(b)-F(a) , называется определенным интегралом . Определённый интеграл - это число, в отличие от неопределённого интеграла, который является группой функций. Крайние точки области интегрирования называются границами интегрирования .Когда интеграл используется для вычисления площади, принято обозначать границы на двух концах знака интеграла и записывать так: .

· Функцию называют первообразной функции .

· -дифференциал функции и определяется следующим образом:

· Формула Ньютона-Лейбница. Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции , то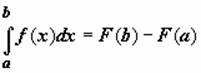

· Уравнение параболы имеет вид y=ax² +bx+c.

· Определенный интеграл численно равен площади под графиком функции от которой он берется, причем площади на интервале интегрирования.

· нахождение неопределенного интеграла это операция обратная нахождению производной(дифференциированию).

4. Расчетная часть.

l=1,5 м

H=2,25 м

1)y=x² +bx+c

2)y=ax² +c

y=ax² -2,25, т.к точка В с координатами (х=0,75;у=0) принадлежит параболе, то её координаты удовлетворяют уравнению параболы. =>

0=а◦0,75² -2,25; 0,75² ◦а=2,25; 0,5625◦а=2,25; а=2,25/0,5625; а=4

3)f(x)=4х² -2,25

4) Найдем площадь «живого сечения»

Т.к части графика 1 и 2 идентичны, можно их представить как 2-е одинаковые части.

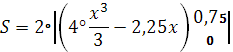
S=2◦2,4375=4,875 м²

Ответ: площадь «живого сечения» 4,875 м³

План:

1. Формулировка проблемы.

2. Пояснение к решению.

3. Графическая часть

4. Расчетная часть.

5. Выводы

6. Используемая литература.

Вывод

Выполнив работу я закрепила знания по теме определенный интеграл, его практическое применение и приложение в реальной жизни. С помощью исходных данных при заданных условиях научилась вычислять «живую площадь» траншеи.

6.Литература

Письменный Д.Т. - Конспект лекций по высшей математике.

Интернет-ресурсы.