Название: Решение практических заданий по дискретной математике

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 215.4 Kb

Скачать файл: referat.me-217807.docx

Краткое описание работы: Представление с помощью кругов Эйлера множественного выражения. Законы и свойства алгебры множеств, упрощение выражений. Система функций, ее возможные базисы. Минимизирование булевой функции. Метод Квайна – Мак-Класки. Определение хроматического числа.

Решение практических заданий по дискретной математике

Содержание

Введение

Задание 1

Представить с помощью кругов Эйлера множественное выражение

Используя законы и свойства алгебры множеств, упростить заданное выражение

Задание 2

Заданы множества кортежей

Показать, что эти множества представляют собой соответствия между множествами N₁ и N₂ , если N₁ = N₂ = . Дать полную характеристику этих соответствий

Задание 3

Частично упорядоченное множество М задано множеством упорядоченных пар

Построить диаграмму и определить, является ли данное множество решеткой. Если заданное множество является решеткой, то определить, является ли решетка дедекиндовой , дистрибутивной …

Задание 4

Является ли полной система булевых функций ? Если система функций полная ,то выписать все возможные базисы

Задание 5

Минимизировать булеву функцию по методу Квайна – Мак-Класки

Задание 6

Для неориентированного графа , у которого ,

а) вычислить числа ;

б) определить хроматическое число …

Задание 7

Для заданной сети :

а) найти величину минимального пути и сам путь от вершины до вершины по алгоритму Дейкстры ;

б) используя алгоритм Форда-Фалкерсона, определить максимальный поток ( v₁ – вход , v₆ – выход сети ) и указать минимальный разрез, отделяющий v₁ от v₆ , если задана матрица весов (длин, пропускных способностей) Р…

Литература

Введение

Проблемы, связанные с понятиями бесконечности, дискретности и непрерывности, рассматривались в математике, как и в философии, древнегреческими мыслителями, начиная с 6 века до нашей эры. Под влиянием сочинений Аристотеля они широко обсуждались средневековыми учеными и философами в странах Европы и Азии. Через всю историю математики проходит идея преодоления между актуальной и потенциальной бесконечностью, с одной стороны, между дискретным характером числа и непрерывной природой геометрических величин – с другой. Впервые проблема математической бесконечности и связанных с нею понятий была широко поставлена в наиболее общем виде в теории множеств, основы которой были разработаны в последней четверти 19 века Георгом Кантором.

Цель контрольной работы – ознакомится с основными понятиями и методами решения по дискретной математике, уметь применить полученные знания при решении практического задания.

Задание 1

Представить с помощью кругов Эйлера множественное выражение

.

Используя законы и свойства алгебры множеств, упростить заданное выражение.

Решение:

Используя круги Эйлера и, учитывая, что операция пересечения выполняется раньше операции объединения, получим следующие рисунки:

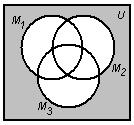
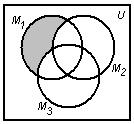
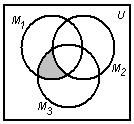
Объединяя заштрихованные области, получим искомое множество:

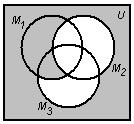
Упростим заданное выражение:

=

.

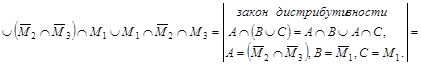
Задание 2

Заданы множества кортежей:

.

Показать, что эти множества представляют собой соответствия между множествами N₁ и N₂ , если N₁ = N₂ = . Дать полную характеристику этих соответствий

Решение:

Найдем декартово произведение:

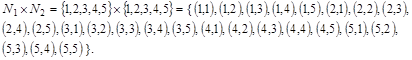
Видно, что заданные множества являются подмножествами этого пря-мого произведения. Следовательно, данные множества есть соответствия.

а) .

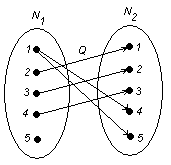
Область определения: . Следовательно, соответствие является частично определенным.

Область значений: . Следовательно, соответствие является сюръективным.

Образом элемента являются два элемента . Значит соответствие не является функциональным. Из этого следует, что соответствие не является функцией, отображением.

б) .

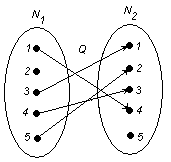
Область определения: . Следовательно, соответствие является частично определенным.

Область значений: . Следовательно, соответствие не является сюръективным.

Образом любого элемента из является единственный элемент из . Следовательно, соответствие является функциональным, функци-ей. Соответствие является частично определенным. Это означает, что функция является частично определенной и не является отображением.

в) .

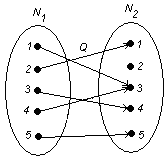
Область определения:.Следовательно, соответствие всюду определено.

Область значений: . Следовательно, соответствие не является сюръективным.

Образом любого элемента из является единственный элемент из . Следовательно, соответствие является функциональным, функцией. Так как соответствие всюду определено, то имеем полностью определенную функцию, т.е. имеем отображение N₁ в N₂ .

г) .

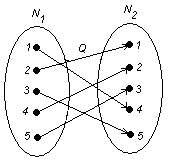
Область определения: . Значит, соответствие полностью определено.

Область значений: . Значит, соответствие сюръективно.

Образом любого элемента из N₁ является единственный элемент из N₂ . Следовательно, соответствие является функциональным, функцией.

Так как соответствие всюду определено, сюръективно, функционально и прообразом любого элемента из является единственный элемент из , то соответствие является взаимно однозначным.

Так как функция полностью определена и соответствие сюръективно, то имеем отображение N₁ на N₂ .

Так как для любых двух различных элементов из N₁ их образы из N₂ также различны, то отображение является инъективным.

Так как отображение является одновременно сюръективным и инъективным, то имеем биективное отображение (взаимно однозначное отображение).

Задание 3

Частично упорядоченное множество М задано множеством упорядоченных пар

.

Построить диаграмму и определить, является ли данное множество решеткой. Если заданное множество является решеткой, то определить, является ли решетка дедекиндовой , дистрибутивной.

Решение:

Построим диаграмму:

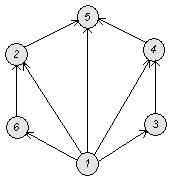
Построим таблицу:

Пары элементов	Н.Г.	В.Г.	Н.Н.Г.	Н.В.Г.
1,2	1	2,5	1	2
1,3	1	3,4,5	1	3
1,4	1	4,5	1	4
1,5	1	5	1	5
1,6	1	6,2,5	1	6
2,3	1	5	1	5
2,4	1	5	1	5
2,5	2,6,1	5	2	5
2,6	6,1	2,5	6	2
3,4	3,1	4,5	3	4
3,5	3,1	5	3	5
3,6	1	5	1	5
4,5	4,3,1	5	4	5
4,6	1	5	1	5
5,6	6,1	5	6	5

Так как любая пара элементов имеет единственную наибольшую нижнюю грань и единственную наименьшую верхнюю грань, то заданное частично упорядоченное множество М является решеткой.

Решетка М является дедекиндовой, когда выполняется равенство:

для таких , что .

Решетка М не является дедекиндовой, т.к. указанное равенство не вы-полняется, например, для элементов 2, 3, 4:

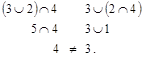
Одним из условий дистрибутивности решетки является ее дедекиндо-вость. Так как решетка М не является дедекиндовой, то она не является дистрибутивной решеткой.

Задание 4

Является ли полной система булевых функций ? Если система функций полная ,то выписать все возможные базисы.

Решение:

Рассмотрим функцию .

1. Принадлежность функции к классу :

.

Следовательно, .

2. Принадлежность функции к классу :

.

Следовательно, .

3. Принадлежность функции к классу .

Предположим, что функция линейная и, следовательно, представима в виде полинома Жегалкина первой степени:

.

Найдем коэффициенты .

Фиксируем набор 000:

,

,

Следовательно, .

Фиксируем набор 100:

,

,

Следовательно, .

Фиксируем набор 010:

,

,

.

Следовательно, .

Фиксируем набор 001:

,

,

, .

Следовательно, функция (по нашему предположению) может быть представлена полиномом вида:

.

Если функция линейная, то на всех остальных наборах ее значение должно равняться 1. Но на наборе 111 . Значит, функция не является линейной, т.е. .

4. Принадлежность функции к классу .

Функция самодвойственная, если на любой паре противоположных наборов (наборов, сумма десятичных эквивалентов которых равна , где п – количество переменных функции) функция принимает противоположные значения.

Вычисляем . Вычисляем значения функции на оставшихся наборах:

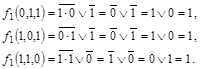
Строим таблицу:

(000) 0	(001) 1	(010) 2	(011) 3	(100) 4	(101) 5	(110) 6	(111) 7
1	1	1	1	1	1	1	0

На наборах 1 и 6, 2 и 5, 3 и 4 функция принимает одинаковые значения. Следовательно, .

5. Принадлежность функции к классу .

Из таблицы видно: 000 < 111 , но . Следовательно, .

Рассмотрим функцию .

1. Принадлежность функции к классу :

.

Следовательно, .

2. Принадлежность функции к классу :

.

Следовательно, .

3. Принадлежность функции к классу .

Предполагаем, что

.

Фиксируем набор 000:

,

.

Фиксируем набор 100:

,

.

Фиксируем набор 010:

,

.

Фиксируем набор 001:

,

.

Окончательно получаем

.

Это равенство не соблюдается на наборе 011:

,

.

Следовательно, .

4. Принадлежность функции к классу .

Вычислим значения функции на оставшихся наборах:

Строим таблицу :

(000) 0	(001) 1	(010) 2	(011) 3	(100) 4	(101) 5	(110) 6	(111) 7
1	1	1	0	0	0	0	0

Из таблицы видно, что на наборах 3 и 4 функция принимает одинаковые значения. Следовательно, .

5. Принадлежность функции к классу .

Из таблицы видно, что 111 > 000 , но . Следовательно, .

Строим критериальную таблицу:

К0	К1	КЛ	КС	КМ
f1	-	-	-	-	-
f2	-	-	-	-	-

В таблице в каждом столбце стоят минусы. Следовательно, система булевых функций

является полной .

Найдем все возможные базисы. По критериальной таблице составим КНФ :

.

Приведем КНФ к ДНФ :

.

По полученной ДНФ выписываем искомые базисы:

.

Задание 5

Минимизировать булеву функцию по методу Квайна – Мак-Класки.

Решение:

1 этап. Определение сокращенной ДНФ.

По десятичным эквивалентам запишем 0-кубы :

Выполним разбиение на подгруппы:

.

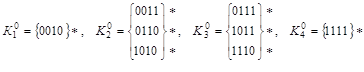Строим -кубы, сравнивая соседние группы (значок (*) указывает на участие данной импликанты в склеивании):

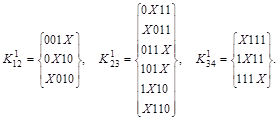
Выполняем разбиение всех -кубов в зависимости от расположения независимой переменной Х :

.

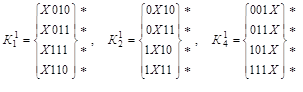Выполняем сравнение кубов внутри каждой подгруппы с целью построения -кубов (значок (*) указывает на участие данной импликанты в склеивании):

.

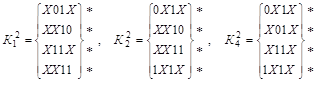Выполняем сравнение кубов внутри каждой подгруппы с целью построения -кубов (значок (*) указывает на участие данной импликанты в склеивании):

или

.

Так как они одинаковы, то .

Запишем сокращенную ДНФ, в которую должны быть включены им-пликанта из К ³ и импликанты, не участвовавшие в склеивании (в нашем случае таких импликант нет) :

.

2 этап. Определение тупиковой ДНФ.

Так как все импликанты участвовали в склеивании, и сокращенная ДНФ состоит из одной простой импликанты, то строить таблицу покрытий нет необходимости, т.е.

.

Задание 6

Для неориентированного графа , у которого ,

а) вычислить числа ;

б) определить хроматическое число .

Решение:

Построим граф:

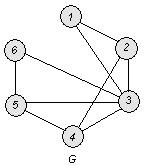
а) Вычислим числа .

1) :

Используя алгоритм выделения пустых подграфов, построим дерево:

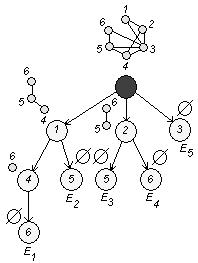
Согласно определению :

.

2) :

Используя алгоритм выделения полных подграфов, построим дерево:

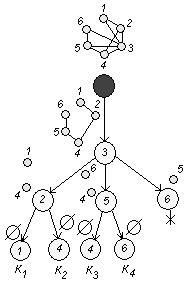
Здесь - полные подграфы. Видно, что мощность носителей всех подграфов равна трем, т.е.

.

3) :

Построим модифицированную матрицу смежности заданного графа G :

1 2 3 4 5 6

.

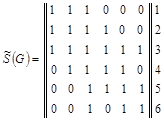
Находим минимальное число строк, покрывающих все столбцы модифи-цированной матрицы . Таких строк – одна. Следовательно,

.

б) Определим хроматическое число .

Согласно алгоритму минимальной раскраски вершин графа, выделим все пустые подграфы графа G , т.е. построим дерево (оно построено в пункте а) ):

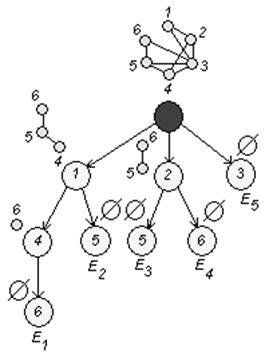
Построим таблицу:

1 2 3 4 5 6

1. {1,4,6} 1 1 1

2. {1,5} 1 1

3. {2,5} 1 1

4. {2,6} 1 1

5. {3} 1

Определяем минимальное число строк, покрывающих все столбцы таблицы. Такими строками могут быть строки 1, 3, 5. Значит,

.

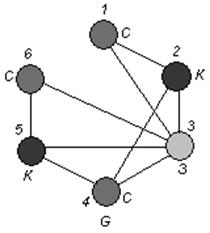
Зададимся красками: для множества вершин - краска синяя (С ), для множества вершин - краска красная ( К ), для множества вершин - краска зеленая ( З ).

Раскрасим вершины графа G :

Задание 7

Для заданной сети :

а) найти величину минимального пути и сам путь от вершины до вершины по алгоритму Дейкстры ;

б) используя алгоритм Форда-Фалкерсона, определить максимальный поток ( v₁ – вход , v₆ – выход сети ) и указать минимальный разрез, отделяющий v₁ от v₆ ,

если задана матрица весов (длин, пропускных способностей) Р :

v₁ v₂ v₃ v₄ v₅ v₆

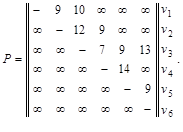
Решение:

Построим сеть:

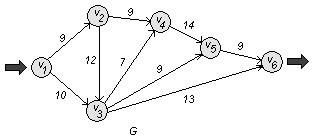
а) Найдем величину минимального пути и сам путь сети G . Используем для этого алгоритм Дейкстры.

Этап 1. Нахождение длины кратчайшего пути.

.

Шаг 1. Полагаем

1-я итерация.

Шаг 2. Составим множество вершин, непосредственно следующих за с временными метками: . Пересчитываем временные метки этих вершин: ,

.

Шаг 3. Одна из временных меток превращается в постоянную:

Шаг 4. Следовательно, возвращаемся на второй шаг.

2-я итерация.

Шаг 2.

Шаг 3.

Шаг 4. Переход на второй шаг.

3-я итерация.

Шаг 2.

Шаг 3.

Шаг 4.

Переход на второй шаг.

4-я итерация.

Шаг 2.

Шаг 3.

Шаг 4. Переход на второй шаг.

5-я итерация.

Шаг 2.

Шаг 3.

Шаг 4. Конец первого этапа.

Следовательно, длина кратчайшего пути равна .

Этап 2. Построение кратчайшего пути.

1-я итерация.

Шаг 5. Составим множество вершин, непосредственно предшествующих с постоянными метками : Проверим равенство

для этих вершин:

т.е.

т.е.

Включаем дугу в кратчайший путь,

Шаг 6. Возвращаемся на пятый шаг.

2-я итерация.

Шаг 5.

Включаем дугу в кратчайший путь, .

Шаг 6. . Завершение второго этапа.

Следовательно, кратчайший путь построен. Его образует последовательность дуг: .

Окончательно, кратчайший путь от вершины до вершины v₆ построен. Его длина (вес) равна . Сам путь образует последовательность дуг:

б) Определим максимальный поток через сеть G. Для этого используем алгоритм Форда-Фалкерсона.

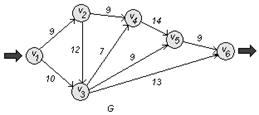
Выбираем произвольно путь из вершины v₁ в вершину v₆ . Пусть это будет путь . Минимальную пропускную способность на этом пути, равную 10, имеет дуга , т.е. Увеличим на этом пути поток до 10 единиц. Дуга становится насыщенной. Дуга имеет на данный момент пропускную способность, равную 10.

Путь Следовательно, поток на этом пути можно увеличить на 9 единиц. Дуги становятся насыщенными.

Других маршрутов нет (другие маршруты проходят через насыщенные дуги). Поток максимален. Делаем разрез вокруг вершины v₁ по насыщенным дугам

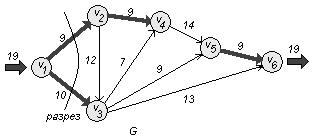
и получаем его величину единиц.

8. Используя алгоритм Краскала, построить остов с наименьшим весом для неориентированного взвешенного графа , у которого , если заданы веса (длины) ребер:

□ Построим граф G :

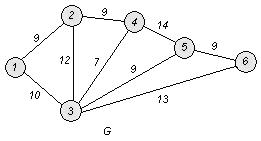
1. Упорядочим ребра в порядке неубывания веса (длины):

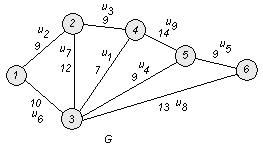
2. Возьмем ребро u₁ и поместим его в строящийся остов.

Возьмем ребро u₂ и поместим его в строящийся остов (т.к. оно не образует с предыдущим ребром цикла).

Берем ребро u₃ и помещаем его в строящийся остов (т.к. оно не образует с предыдущими ребрами цикла).

Берем ребро u₄ и помещаем его в строящийся остов (т.к. оно не образует с предыдущими ребрами цикла).

Берем ребро u₅ и помещаем его в строящийся остов (т.к. оно не образует цикла с предыдущими ребрами).

Ребра не рассматриваем, т.к. они образуют циклы с предыдущими ребрами.

Проверим окончание алгоритма. Число входящих в остов ребер равно 5. Заданный граф имеет п = 6 вершин и . Таким образом, остов содержит все вершины заданного графа G .

Вес (длина) построенного остова

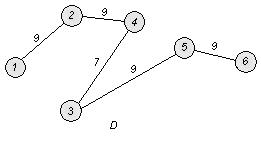
равен .

Литература

1. Горбатов В.А. Основы дискретной математики. – М.: Высшая школа, 1986. – 311 с.

2. Коршунов Ю.М. Математические основы кибернетики. – М.: Энерго атомиздат, 1987. – 496 с.

3. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988. – 480 с.

4. Шапорев С.Д. Дискретная математика. – СПб.: БХВ-Петербург, 2006. - 400 с.

5. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике. – М.: ФИЗМАТЛИТ, 2005. – 416 с.

6. Хаханов В.И., Чумаченко С.В. Дискретная математика ( конспект теоретического материала). – Харьков: ХНУРЭ, 2003. – 246 с.

7. Богданов А.Е. Курс лекций по дискретной математике.–Северодонецк: СТИ, 2006. – 190 с.