Referat.me / Математика / Решение задачи про кондитерскую фабрику

Название: Решение задачи про кондитерскую фабрику

Вид работы: реферат

Размер файла: 733.41 Kb

Скачать файл: referat.me-217936.docx

Краткое описание работы: Задание 1 Маленькая кондитерская фабрика должна закрыться на реконструкцию, поэтому надо реализовать оставшиеся запасы сырья, получив максимальную прибыль. Запасы и расход сырья для производства единицы продукции каждого вида, а также получаемая при этом прибыль представлены в таблице.

Решение задачи про кондитерскую фабрику

Задание 1

Маленькая кондитерская фабрика должна закрыться на реконструкцию, поэтому надо реализовать оставшиеся запасы сырья, получив максимальную прибыль. Запасы и расход сырья для производства единицы продукции каждого вида, а также получаемая при этом прибыль представлены в таблице.

Ресурсы	Кондитерские изделия					Ограничения
Ресурсы	Ореховый звон	Райский вкус	Батончик	Белка	Ромашка	Ограничения
Темный шоколад	0,8	0,5	1	2	1,1	1411
Светлый шоколад	0,2	0,1	0,1	0,1	0,2	149
Сахар	0,3	0,4	0,6	1,3	0,05	815,5
Карамель	0,2	0,3	0,3	0,05	0,5	466
Орехи	0,7	0,	0,9	0,5	0	1080
Прибыль	1	0,7	1,1	0,6	0,6

Мастер, используя свой 20-летний опыт, предлагает «на глазок» выпустить по 200 пакетов каждого продукта, утверждая, что ресурсов должно хватить, а прибыль получится 1080 у.е. Сын владельца фабрики, только что прошедший курсы по математическому моделированию, утверждает, что такие проблемы надо решать с помощью линейного программирования. Отец обещает сыну всю прибыль сверх 1080 у.е., если он предложит лучший план, чем опытный мастер.

Требуется:

1) определить оптимальный план выпуска продукции. Какую прибыль планирует получить сын?

2) проанализировать использование ресурсов в оптимальном плане.

Экономико-математическая модель задачи.

Пусть x - число изделий «Ореховый звон»; x - число изделий «Райский вкус»; x- число изделий «Батончик»; x - число изделий «Белка» x- число изделий «Ромашка»;

f(x) = 1*x+0,7* x+1,1*x+2* x+ 0,6* x max.

Ограничения задачи имеют вид:

x+ x+ x+ x+ x 1411 – ограничение по темному шоколаду;

x+ x+ x+ x+ x 149 – ограничение по светлому шоколаду;

x+ x +x+ x+ x 815,5 – ограничение по сахару;

x+ x+ x+ x+ x 466 – ограничение по карамели;

x+ x+ x+ x+ x 1080 – ограничение по орехам;

Решение.

Вводим исходные данные и зависимость для целевой функции, в нашем случае это ячейка F3.

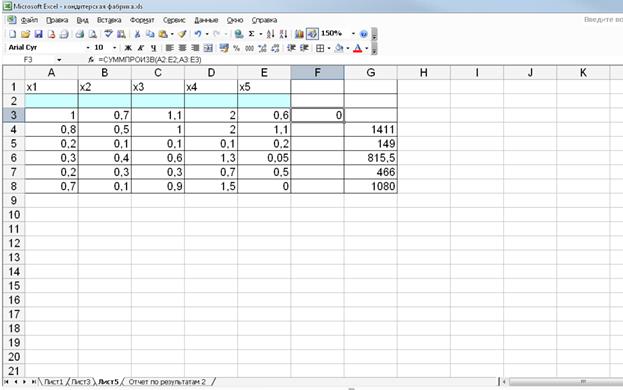
Запускаем Поиск решения и вводим все данные в открывшееся окно:

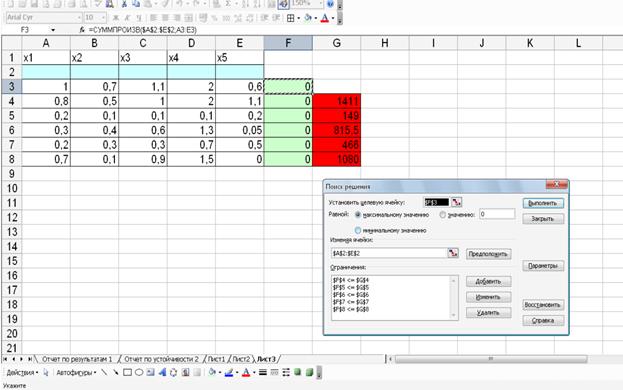
Выбираем нужные параметры:

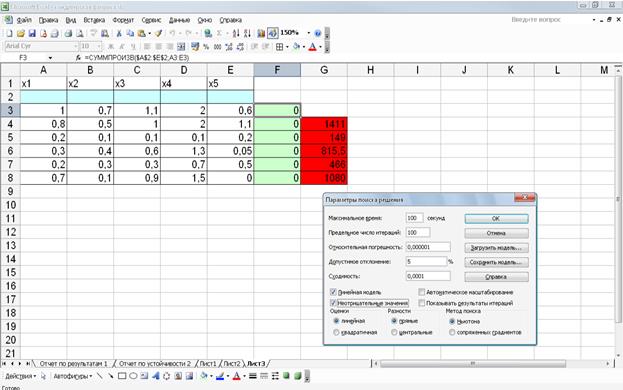
Выполняем поиск решения и получаем результат.

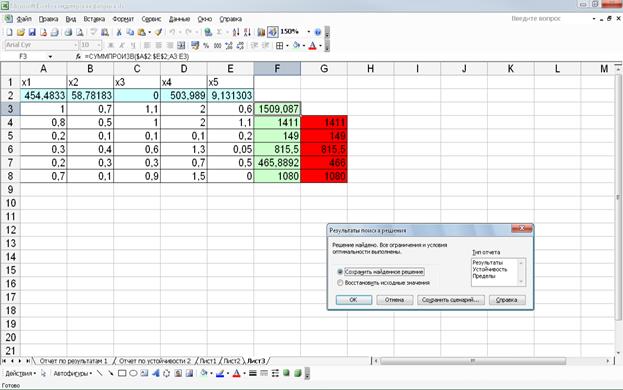
В результате решения задачи был получен ответ: нужно выпустить 454 пак. изделия «Ореховый звон», 58 пак. изделия «Райский вкус», 504 пак. изделия «Белка», 9 пак. изделия «Ромашка». Выпуск же изделия «Батончик» не понадобится. Прибыль, полученная в результате создания оптимального плана выпуска продукции кондитерской фабрикой составила 1509 у.е.

Отчет по результатам.

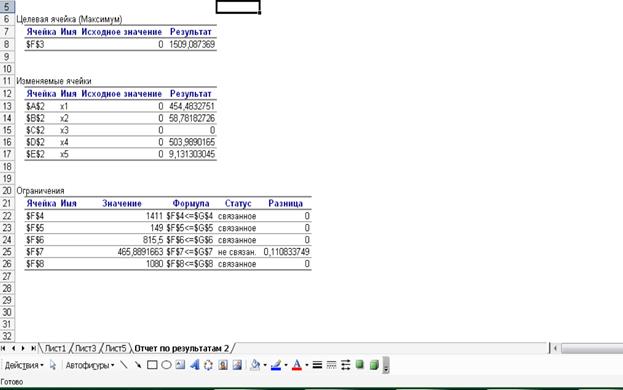
Из отчета видно, какая прибыль была получена, каких изделий и в каком количестве необходимо выпустить, а также оптимальное использование ресурсов. Из последнего можно сделать вывод, что четыре ресурса были полностью использованы. По ресурсу же «Карамель» имеет место недоиспользование на 0,11.

Решение задачи про кондитерскую фабрику

Похожие работы