Название: Математические последовательности Предел функции

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 220.41 Kb

Скачать файл: referat.me-218096.docx

Краткое описание работы: Задание 1 Вычислите последовательности Решение. Рассмотрим последовательность для любого натурального Следовательно, множество является ограниченным сверху. Это означает, что последовательность

Математические последовательности Предел функции

Задание 1

Вычислите и последовательности .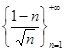

Решение.

Рассмотрим последовательность .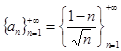

для любого натурального

Следовательно, множество 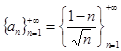является ограниченным сверху. Это означает, что последовательность 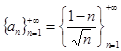имеет верхнюю точную грань: .

Следовательно, множество 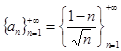не является ограниченным снизу. Это означает, что нижняя грань последовательности 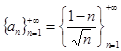не существует.

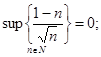
Ответ. 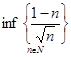не существует

Задание 2

Пользуясь определением предела последовательности, докажите, что .

Доказательство.

Число называется пределом последовательности , если для любого положительного числа существует номер такой, что при выполняется неравенство .

Используя определение предела последовательности, докажем, что .

Возьмем любое число .

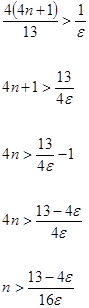
Если взять , то для всех будет выполняться неравенство . Следовательно, .

Доказано

Задание 3

Пользуясь определением предела функции, докажите, что .

Доказательство

Число называется пределом функции при , если для любого числа существует число такое, что для всех , удовлетворяющих неравенству , выполняется неравенство .

Используя определение предела функции, докажем, что .

Возьмем любое .

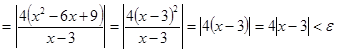
Положим .

Если взять , то для всех , удовлетворяющих неравенству , выполняется неравенство . Следовательно, .

Доказано.

Задание 4

Вычислите предел .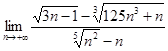

Решение.

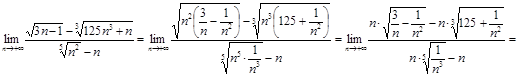
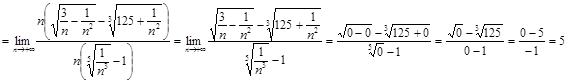
Ответ.

Задание 5

Вычислите предел .

Решение.

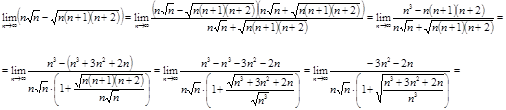
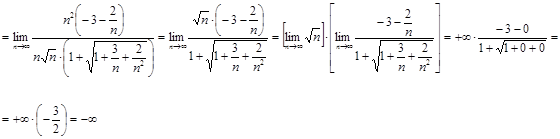
Ответ.

Задание 6

Вычислить предел .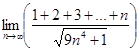

Решение.

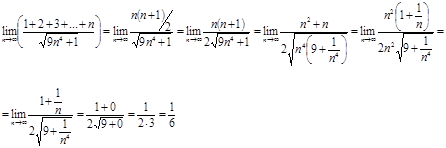
Ответ.

Задание 7

Вычислить предел .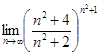

Решение.

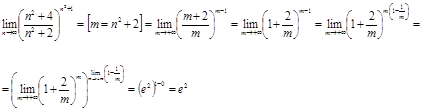
Ответ.

Задание 8

Вычислить предел .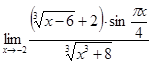

Решение

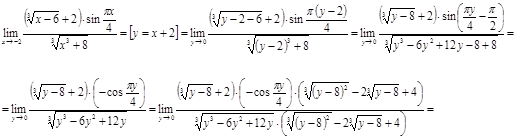
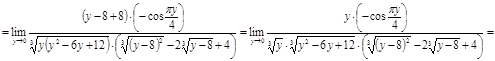
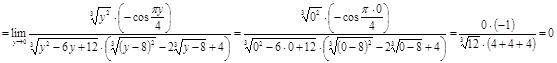
Ответ.

Задание 9

Вычислить предел .

Решение.

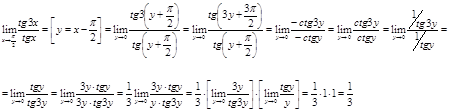
Ответ.

Задание 10

Вычислить предел .

Решение.

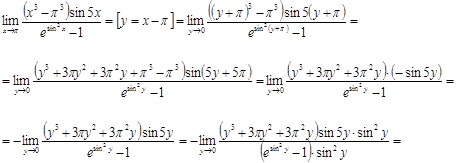
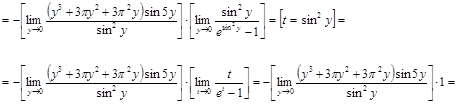
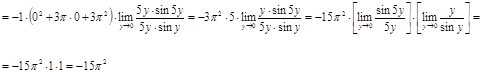
Ответ.

Задание 11

Вычислить предел .

Решение.

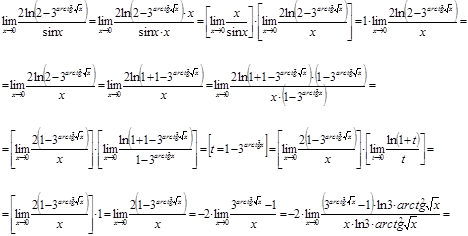
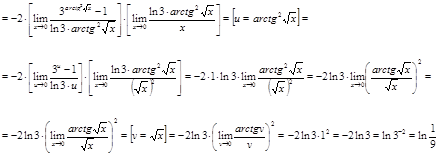
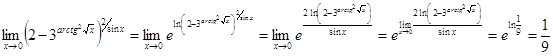
Ответ.

Задание 12

Вычислить предел .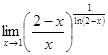

Решение.

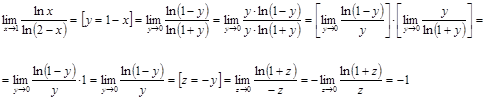
Ответ.

Задание 13

Вычислить предел .

Решение.

Ответ.

Задание 14

Вычислить предел .

Решение.

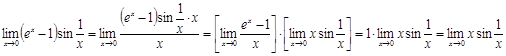
при функция является бесконечно малой

для любого функция является ограниченной.

Известно, что произведение бесконечно малой функции и ограниченной функции есть бесконечно малая функция. Следовательно, функция является бесконечно малой при . Это означает, что .

Ответ.