Название: Пифагор 3

Вид работы: реферат

Рубрика: Математика

Размер файла: 95.31 Kb

Скачать файл: referat.me-218553.docx

Краткое описание работы: Бексултанова Дания Шокановна ОКШДС № 77 Г. Караганда Шокенова З.У. геометрия Пифагор. Теорема Пифагора. русский Требуется компьютер ПИФАГОР. ФИЛОСОФ И МАТЕМАТИК, ПОЛИТИК И РЕЛИГИОЗНЫЙ ЛИДЕР

Пифагор 3

1.	Бексултанова
2.	Дания
3.	Шокановна
4.	10 Г
5.	ОКШДС № 77
6.	Г. Караганда
7.	Шокенова З.У.
8.	геометрия
9.	Пифагор. Теорема Пифагора.
10.	русский
11.	Требуется компьютер

ПИФАГОР. ФИЛОСОФ И МАТЕМАТИК, ПОЛИТИК И РЕЛИГИОЗНЫЙ ЛИДЕР

Бексултанова Д.Ш.

10 Г , ОКШДС № 77, г. Караганда

рук. Шокенова З.У.

О Пифагоре : Пифагор жил в шестом веке до нашей эры, имел красивую внешность, носил длинную бороду, а на голове золотую диадему. Пифагор - это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор - "убеждающий речью".) Своими речами приобрёл 2000 учеников, которые вместе со своими семьями образовали школу-государство, где действовали законы и правила Пифагора.

Он был первым человеком, который назвал себя философом. До него умные люди называли себя гордо и несколько высокомерно - мудрецами, что означало - человек, который знает. Пифагор же назвал себя философом - тем, кто пытается найти, выяснить. Слово "философ", как и слово "космос" достались нам от Пифагора. Всё в природе, говорил Пифагор, разделено на три части. Поэтому прежде чем решать любую проблему, её надо представить в виде треугольной диаграммы. "Узрите треугольник - и задача на две трети решена".Пифагор стоял у истока греческой науки, он был вынужден заниматься всем сразу: арифметикой и геометрией, астрономией и музыкой. Его целью было разобраться в строении Вселенной и человеческого общества (от движения звезд до политической борьбы).

Открытие Пифагора: Он первый заметил, что сила и единство науки основаны на работе с идеальными объектами. Например, прямая линия – это тетива натянутого лука и не луч света: ведь они имеют небольшую толщину, а линия толщины не имеет. Несовершенные природные тела являются лишь грубоватым подобием идеальных математических сущностей. Первая научная модель мира, предложенная Пифагором – все природные тела и процессы суть искаженные подобия идеальных тел и движений – а закономерности идеальных объектов выражаются с помощью чисел. «Числа правят миром через свойства геометрических фигур»

Теорема Пифагора (Пифагоровы штаны): Пифагоровы штаны - шуточное название теоремы Пифагора, возникшее в силу того, что раньше в школьных учебниках эта теорема доказывалась равенства суммы площадей квадратов, построенных на катетах прямоугольного треугольника, площади квадрата построенного на гипотенузе этого треугольника. Построенные на сторонах треугольника и расходящиеся разные стороны квадрата напоминали школьникам покрой мужских штанов, что породило следующее стихотворение : «Пифагоровы штаны – на все стороны равны».

Доказательство теоремы Пифагора:

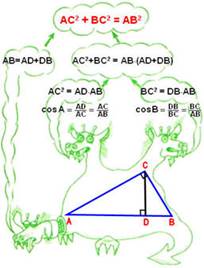Провели Δ АВС высоту С D , и образовал ось два новых прямоугольных треугольника ADC и BDC .

Древние египтяне более 2000 лет тому назад практически пользовались свойствами треугольника со сторонами 3, 4, 5 для 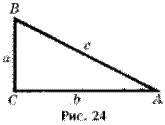построения прямого угла, т. е. фактически применяли теорему, обратную теореме Пифагора. Приведем доказательство этой теоремы, основанное на признаке равенства треугольников (т. е. такое, которое можно очень рано ввести в школе). Итак, пусть стороны треугольника ABC (рис. 24) связаны соотношением

c² = a² + b² . (1)

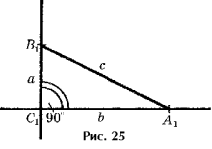Докажем, что этот треугольник прямоугольный. Построим прямоугольный треугольник A₁ B₁ C₁ по двум катетам, длины которых равны длинам a и b катетов данного треугольника (рис. 25). Пусть длина гипотенузы построенного треугольника равна c₁ . Так как построенный треугольник прямоугольный, то по теореме Пифагора имеем: c₁ ² = a² + b² . (2)

Сравнивая соотношения (1) и (2), получаем, что

c₁ ² = c² , или c₁ = c.

Таким образом, треугольники – данный и построенный – равны, так как имеют по три соответственно равные стороны. Угол C₁ прямой, поэтому и угол C данного треугольника тоже прямой.

Пифагорейцы:

Пифагорейцы образовали большое сообщество(их было более трёхсот), но она составляло лишь небольшую часть города, который уже не управлялся согласно тем же обычаям и нравам. Пифагорейцы приписывали числам различные свойства.Так, четные числа они называли женскими, нечетные (кроме 1) - мужскими. Число 5 - как сумма первого женского числа (2) и первого мужского (3) - считалось символом любви.Они же выделили понятие простого числа. Им были знакомы три вида пропорций:

арифметическая (a-b):(b-c)=a:a;

геометрическая (a-b):(b-c)=a:b;

гармоническая (a-b):(b-c)=а:c.

Пифагорейцы доказали, что сумма углов треугольника равна сумме двух прямых углов; установили, что плоскость можно "замостить" правильными многоугольниками так, что вокруг одной точки будут лежать или шесть треугольников, или четыре квадрата, или три шестиугольника.

Десять правил Пифагора:

-Отклоняйся от дорог исхоженных, используй нехоженые пути;

-Будь хозяином своему языку прежде всех других вещей, следуя при этом Богу;

- Дует ветер - поклоняйся шуму

- Помогай человеку в поднятии тяжести, но не помогай в сложении ее

- Выйдя из дома своего, - не возвращайся ..

- Не говори о делах учения без Света.

- Корми петуха, но не приноси его в жертву, поскольку он посвящен Солнцу и Луне

- Не позволяй ласточкам селиться в твоем доме

- Не протягивай охотно свою правую руку никому.

- Поднявшись с постели, - сгладь отпечатки тела.

На первый взгляд этот свод правил напоминает мистическое руководство из мира суеверий, но по всей видимости, слова Пифагора нельзя понимать буквально, в прямом смысле. За каждым из изречений стоит скрытый тайный смысл, а какой пусть каждый решит для себя сам.

Теорема Пифагора в стереометрии:

1)В стереометрии известен аналог теоремы Пифагора для треугольного параллелепипеда d²=a²+b²+c², где d- диагональ параллелепипеда a,b,c – величина трех его измерений.

2)В прямоугольной пирамиде квадрат площади гипотенузы равен сумме квадратов площадей катетов.

Следствия теоремы Пифагора:

1)В прямоугольном треугольнике любой из катетов меньше гипотенузы.

2)В прямоугольном пирамиде площадь любого из катетов меньше площади гипотенузы.

3)Если прямоугольном треугольнике АВС, к гипотенузе проведена высота СD=h,делящая её на отрезки x и y,то H²=xy.

4) В прямоугольной пирамиде аналог высоты это треугольник СОН (СН ┴ АВ), Н²= XYsinφ.

5)Площадь прямоугольного треугольника равна половине произведения его катетов.

6)Объем прямоугольной пирамиды равняется 1/6√a²b²c², где а=ОА, b=OB, c=OC.ребра треугольной пирамиды ОАВС, у которой все плоские углы, при вершине О прямые.

Прямоугольный треугольник и прямоугольная пирамида

Возьмем в пространстве произвольный треугольник АВС и ортогонально спроектируем его на плоскость β, проходящую через одну из его сторон, например сторону АВ. Пусть угол между плоскостями АВС и β равен φ (рис. 1.)

Тогда не трудно доказать, что

S∆ABC = S∆ABC cosφ (1)

Формула (1) позволяет определить тригонометрические функции двугранного угла, не сводя их к тригонометрическим функциям плоского угла.

Заметим, что прямоугольном треугольнике ВСО (∟О = 90˚) верно равенство ВО=ВСсоsφ (2)

Формулы (1) и (2) похожи, только в первом случае мы брали треугольник и его проекцию, а во втором – гипотенузу и катет, прилежащий к углу α. Эти формулы приводят к мысли, что прямоугольный треугольник ВСО аналогичен пирамиде ОАВС.

При встрече с прямоугольным треугольником сразу же вспоминается теорема Пифагора. Выясним, справедлива ли подобная теорема для прямоугольной пирамиды.

Замечание. В стереометрии известен аналог теоремы Пифагора для прямоугольного параллелепипеда: d² = a² + b² + c², где d – диагональ параллелепипеда, а a,b,c – величины трех его измерений.

В прямоугольной пирамиде ОАВС АО=а, ВО=b, СО=с. По аналогии с теоремой Пифагора должно выполняться следующее равенство:

S²∆ABC = S²∆COA + S²∆COB +S²∆AOB.

Представив в эту формулу равенство (1) и сделав некоторые преобразования, получим

S²∆AOB · tg²φ = S²∆COA + S²∆COB (3).

В прямоугольном треугольнике СОН tgφ = СО/ОН, по условию СО=с, а ОН найдем из треугольников АОВ и АНО. В одном sinα = ОВ/АВ? А на другом sinα = ОН/АО. Таким образом получаем равенство ОВ/АВ = ОН/АО, откуда ОН = ОВ·АО/АВ.

В прямоугольном треугольнике АОВ АВ = √a² + b².Остальные даные есть в условии, в результате ОН = ab/√a² + b², а tgφ = c/√a² + b²/ab.

Площади прямоугольных треугольников АОВ, СОА и СОВ равны соответственно ab/2, aс/2 и bс/2. В результате формула (3) приобретает вид

a²b² / 4 · с²( a²+b²) / a²b² = a²с² /4 + b²с²/4;

преобразовав её, получим

с²( a²+b²) = с²( a²+b²).

Последнее выражение является верным равенством, поэтому можно сделать вывод: первоначальное предположение было верным и верна теорема.

Теорема. В прямоугольной пирамиде квадрат площади гипотенузы равен сумме квадратов площадей катетов.

Следствие теоремы Пифагора и её анализ

- В прямоугольном треугольнике любой из катетов меньше гипотенузы.

В прямоугольной пирамиде площадь любого из катетов меньше площади гипотенузы.

- Если в прямоугольном треугольнике АВС к гипотенузе проведена высота СD = h, делящая её на отрезки x и y h² = хỵ

В прямоугольной пирамиде (рис.2) аналог высоты - это треугольник СОН (СН ┴АВ). Обозначим S∆COН =Н, S∆CАН = Х, S∆CBН = У.

Тогда Н² = ¼ ОН² · ОС².

Заменим, ОН² на произведение АН и НВ, а ОС² - на sinφ ·CH² и получим

Н² = 1/2 АН² · СН1/2 НВ · СН · sin²φ.

В результате выражение принимает вид

Н² = Х · У · sin²φ.

- Площадь прямоугольного треугольника равна половине произведения его катетов, т.е. S =1/2ab. Чтобы получить аналог этого свойства, выразим объем прямоугольной пирамиды через произведение площадей её катетов. Для удобства примем за основание пирамиды грань АОВ, тогда

V = 1/3·ab/2·c = 1/6abc = 1/6√a²b²c² = 2√2/6·√ab/2·bc/2·ac/2

V = √2/2·√ S∆AOB · S∆BOC · S∆АОС

- Аналог теоремы косинусов для прямоугольной пирамиды: в прямо-угольной пирамиде ОАВС выполняется равенство (рис.2)

S²∆AОС + S²∆ВОС = S²∆АВС + S²∆AOB - 2S²∆·S²∆AOB cos φ (4),

где φ – это двугранный угол между гранями АВС и АОВ.

Литература:

1. « Краткий справочник школьника»;

2. Глейзер Г.И. « История математики в школе» ,1982;

3. Еленьский Щ. «По следам Пифагора», 1961.

4. Погорелов А.В. «Геометрия 7-11 класс», 1992.