Название: Типовой расчет

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 183.97 Kb

Скачать файл: referat.me-218892.docx

Краткое описание работы: Условия и анализ заданий по математике: найти сумму ряда, область сходимости функционального ряда, исследовать ряд на сходимость, вычислить сумму ряда с точностью альфа, используя метод неопределённых коэффициентов, признак Даламбера и признак Лейбница.

Типовой расчет

1. Найти сумму ряда:

Решение.

Разложим знаменатель на множители.

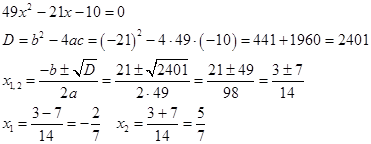
Значит,

Разложим дробь , используя метод неопределённых коэффициентов.

то есть:

, ,

Следовательно,

Тогда, исходный ряд примет вид:

Найдём n – первые членов ряда, записывая дроби с одинаковыми знаменателями друг под другом:

=

=

=

=

=

=

=

=

Сложим n – первых членов ряда и найдём их сумму.

.

Тогда искомая сумма равна:

.

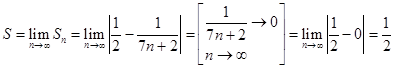Ответ: .

2. Найти сумму ряда:

Решение.

Разложим дробь , используя метод неопределённых коэффициентов.

то есть:

, , ,

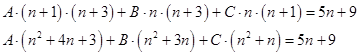
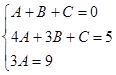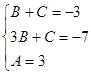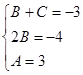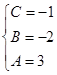
Следовательно,

Тогда, исходный ряд примет вид:

Найдём n – первых членов ряда , записывая дроби с одинаковыми знаменателями, друг под другом:

=

=

=

=

=

=

=

=

Сложим n – первых членов ряда

и найдём их сумму.

.

Тогда искомая сумма равна:

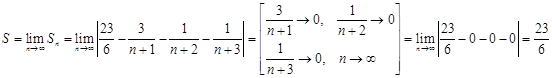
Ответ: .

3. Исследовать ряд на сходимость

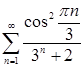
Решение.

Так как , то рассмотрим ряд

, тогда

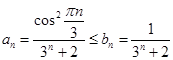
Воспользуемся признаком Даламбера.

,

Тогда,

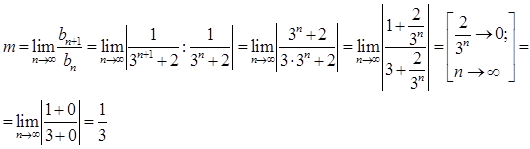
Так как , то ряд сходится. Значит, исходный ряд 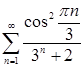сходится по теореме о сравнении рядов.

Ответ: Ряд 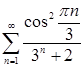сходится.

4. Исследовать ряд на сходимость

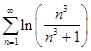
Решение.

Преобразуем n – член этого ряда.

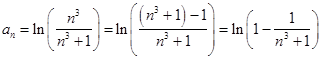
Сравним ряд с рядом , пользуясь предельным признаком сравнения:

,

Тогда,

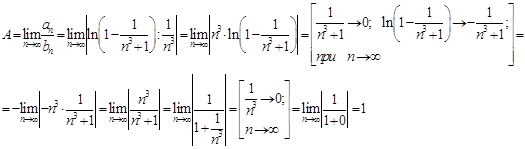
Поскольку А = 1 (0<A<+∞) – действительное число. Следовательно, ряды либо сходятся, либо расходятся. Ряд - является рядом Дирихле. Так как α = 3 > 1, то данный ряд сходится. Следовательно, и сравниваемый ряд 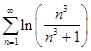тоже сходится.

Ответ: ряд 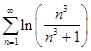сходится.

5. Исследовать ряд на сходимость

Решение.

Воспользуемся признаком Даламбера.

,

Находим m по формуле:

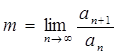
Тогда:

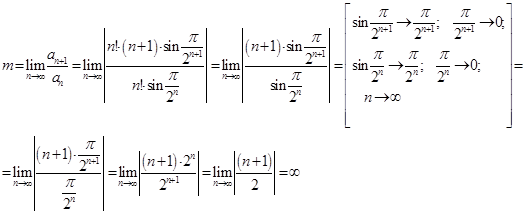
Так как , то ряд 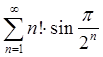расходится.

Ответ: ряд 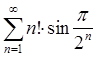расходится.

6. Исследовать ряд на сходимость

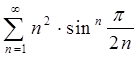
Решение.

Рассмотрим ряд

.

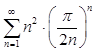Поскольку при :

Воспользуемся признаком Даламбера.

,

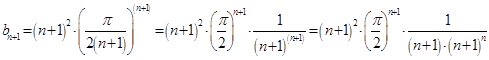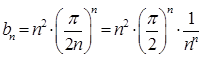
Находим m по формуле:

Тогда:

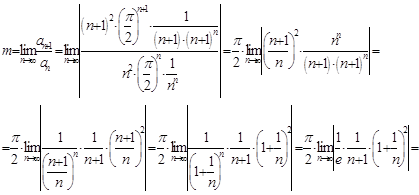
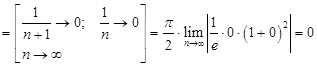
Так как , то ряд 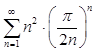сходится.

Согласно признаку сравнения сходится и ряд .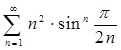

Ответ: ряд 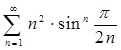сходится.

7. Вычислить сумму ряда с точностью α..

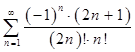α. = 0,001.

Решение.

Прежде чем находить сумму ряда необходимо убедиться, что данный ряд сходится. Проверим исходный ряд на сходимость.

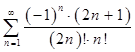- числовой знакочередующейся.

Воспользуемся признаком Лейбница:

1)

2)

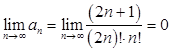
Следовательно, ряд 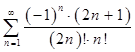условно сходится.

Проверим абсолютную сходимость ряда 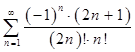. Рассмотрим ряд .

Воспользуемся признаком Даламбера:

,

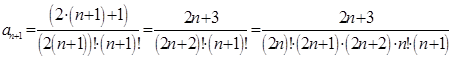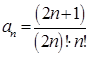
Находим m по формуле:

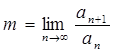
Тогда: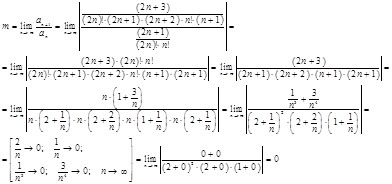

Следовательно, ряд

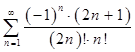сходится абсолютно.

Вычисляем члены ряда с точностью до 4 цифр после запятой до тех пор, пока какой-нибудь член ряда по модулю не будет меньше α. = 0,001:

а₁ = -1,5 а₂ = 0,1042 а₃ = - 0,0016 а₄ = 0,0000093

Для приближённого вычисления ряда достаточно первых трех членов ряда (по следствию признака Лейбница: сумма сходящегося знакопеременного числового ряда не превышает его первого члена). Следовательно, ошибка при вычислении не превысит 0,0000093, а, значит, и . Требуемая точность достигнута.

Следовательно:

.

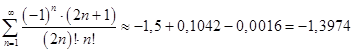Ответ: .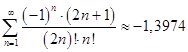

8. Найти область сходимости функционального ряда

Решение.

Рассмотрим два интервала:

1)

Проверим необходимый признак сходимости рядов:

Необходимый признак не выполняется. Следовательно, при ряд расходится.

2) , то есть

Проверим необходимый признак сходимости рядов:

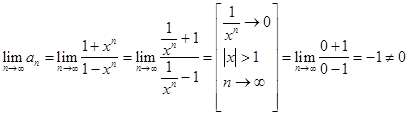
Необходимый признак не выполняется. Следовательно, при ряд расходится.

При имеем:

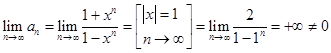
то есть ряд расходится.

Окончательно, получаем ряд расходится при любом Х

Ответ:

9. Найти область сходимости функционального ряда

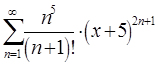
Решение.

Воспользуемся признаком Даламбера:

.

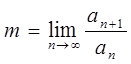В данном примере:

,

.

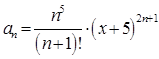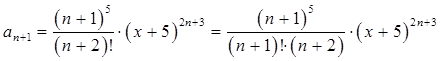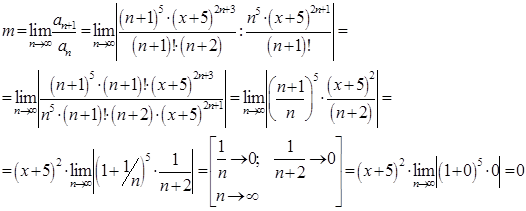
Следовательно, ряд 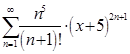сходится при любом Х, т.е.

Ответ: .

10. Найти сумму ряда:

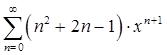
Решение.

Найдём область абсолютной сходимости ряда, пользуясь признаком Даламбера:

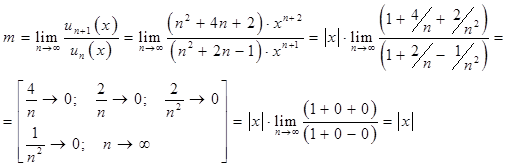
то есть . Ряд сходится для тех значений Х, для которых , то есть , .

При ряд расходится, так как .

Следовательно, .

Перепишем данный ряд:

Обозначим сумму трёх рядов через , и соответственно, тогда

.

Определяем область сходимости этих рядов, пользуясь признаком Даламбера:

1) :

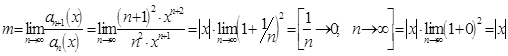
то есть . Ряд сходится для тех значений Х, для которых , то есть , .

Следовательно, .

2) :

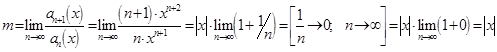
то есть . Ряд сходится для тех значений Х, для которых , то есть , .

Следовательно, .

3) :

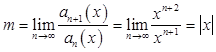
то есть . Ряд сходится для тех значений Х, для которых , то есть , .

Следовательно, .

Найдём сумму ряда .

Это сумма бесконечной геометрической прогрессии: , тогда:

.

Найдём сумму ряда .

.

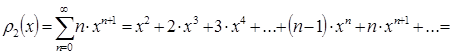
Обозначим сумму ряда в скобках за и проинтегрируем:

.

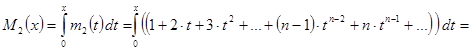
Продифференцируем :

.

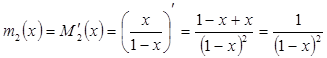Отсюда:

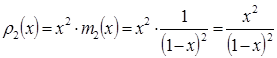
сумму ряда .

.

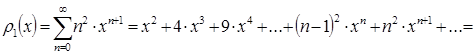
Обозначим сумму ряд в скобках за и проинтегрируем:

.

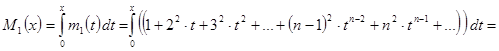
Тогда, продифференцируем :

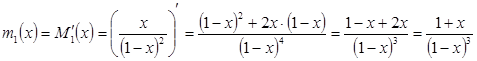
Отсюда:

.

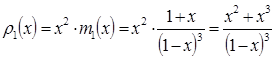Следовательно:

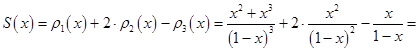
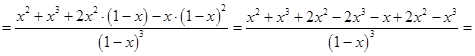
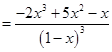для всех .

Ответ: 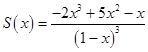для всех .