Referat.me
/ / Решения к Сборнику заданий по высшей математике Кузнецова Л.А. - 2. Дифференцирование. Зад.10

Название: Решения к Сборнику заданий по высшей математике Кузнецова Л.А. - 2. Дифференцирование. Зад.10

Вид работы: реферат

Рубрика: Астрономия

Размер файла: 69.54 Kb

Скачать файл: referat.me-3860.docx

Краткое описание работы: Задача 10 . Найти производную. 10.1. y'= 1 *2-√5thx*√5/ch2x*(2-√5thx)+ √5/ch2x*(2+√5thx) = 4√5 2+√5thx (2-√5thx)2

Решения к Сборнику заданий по высшей математике Кузнецова Л.А. - 2. Дифференцирование. Зад.10

Задача 10 . Найти производную.

10.1.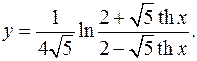

y'= 1 *2-√5 thx *√5/ ch 2 x *(2-√5 thx )+ √5/ ch 2 x *(2+√5 thx ) =

4√5 2+√5thx (2-√5thx)2

= 1 _

ch2 x(2-√5thx)

10.2.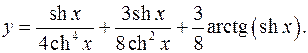

y'= ch5 x-4ch3x sh2 x + 3ch3 x-6chxsh2 x + 3chx = 1 + 3-3sh2 x + 3 _

4ch8 x 8ch4 x 8(1+sh2 x) 4ch5 x 8ch3 x 8chx

10.3.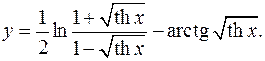

1-√(thx) + 1+√(thx) _

y'= 1/2* 1-√(thx) * 2√(thx)ch2 x 2√(thx)ch2 x _ 1 =

1+√(thx) (1-√(thx))2 2√(thx)ch2 x

= √thx _

(1-th2 x)(ch2 x)

10.4.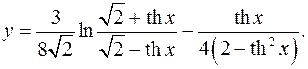

√2-thx + √2+thx 2-th2 x + 2th2 x

y'= 3 *√2-thx * ch2 x ch2 x _ ch2 x ch2 x =

8√2 √2+thx (√2-thx)2 4(2-th2 x)2

= 1 _

2ch2 x(2-th2 x)2

10.5.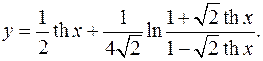

y'= 1 + 1-√2 thx * √2(1-√2thx+1+√2thx) =

2ch2 x 4√2(1+√2thx) ch2 x(1-√2thx)2

= 1-th2 x _

ch2 x(1-√2thx)2

10.6.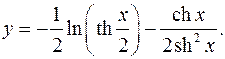

y'= _ 1 _ sh3 x-2shxch2 x = 2ch3 x+2chx-sh2 x

4thxch2 x 2sh4 x 4sh3 xchx

10.7.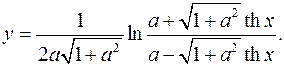

y'= a-√(1+a2 )thx * √(1+a2 )thx(a-√(1+a2 )thx+a+√(1+a2 )thx) =

2a√(1+a2 )(a+√(1+a2 )thx) (a-√(1+a2 )thx)2

= thx = thx = thx _

(a2 -(1+a2 )th2 x)ch2 x a2 ch2 x-(1+a2 )sh2 x a2 -sh2 x

10.8.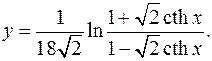

y'= 1-√2cthx * √2(-1+√2cthx+1+√2cthx) = √2cthx =

18√2(1+√2cthx) sh2 x(1-√2cthx)2 9sh2 x(1-√2cthx)

= -√2cthx _

9(1+ch2 x)

10.9.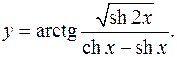

y'= 1 * ch2x/√(sh2x)-√(sh2x)(shx-chx) =

1+sh2x/(shx-chx)2 chx-shx

= (chx-shx)(ch2x-sh2x(shx-chx))

√(sh2x)(ch2 x+sh2 x)

10.10.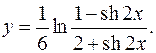

y'= 2+sh2x * -ch2x(2+sh2x)-ch2x(1-sh2x) = ch2x _

6(1-sh2x) (2+sh2x)2 12-6sh2x-sh2 2x

10.11.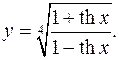

y'= 4 √(1-thx)3 * 1-thx+1+thx = 1 _

44 √(1+thx)3 ch2 x(1-thx) 4ch2 x√(1+thx) 4 √(1-th2 x)

10.12.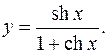

y'= chx(1+chx)-sh2 x = 1 _

(1+chx)2 1+chx

10.13.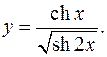

y'= shx√(sh2x)-chxch2x/√(sh2x) = shx-chxcth2x

sh2x

10.14.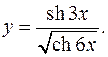

y'= 3ch3x√(ch6x)-3sh6xsh3x/√(ch6x) = 3sh3x-3th6xsh3x

ch6x

10.15.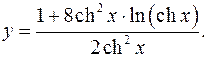

y'= 16shxch3 x*ln(chx)+8ch3 xshx-16ch3 xshxln(chx) = 4thx

2ch4 x

10.16.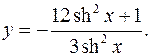

y'= 2shxchx(12sh2 x+1)-24sh3 xchx = 4chx

3sh4 x 3sh3 x

10.17.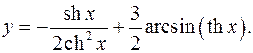

y'= 2chxsh2 x-ch3 x + 3 = shx-1 + 3 _

2ch4 x ch2 x√(1-th2 x) 2ch3 x ch2 x√(1-th2 x)

10.18.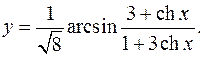

y'= 1 * shx(1+3chx)-3shx(3+chx) =

√8√(1-(3+chx)2 /(1+3chx)2 ) (1+3chx)2

= -8shx = -1 _

8(1+3chx)√(ch2 x-1) 1+3chx

10.19.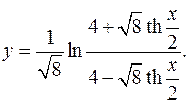

y'= 4-√8th(x/2) * √8(4-√8th(x/2)+4+√8th(x/2)) =

√8(4+√8th(x/2)) 2ch2 (x/2)(4-√8th(x/2))2

= 1 _

ch2 (x/2)(4-√8th(x/2))

10.20.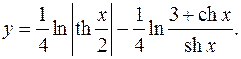

y'= 1 _ shx(sh2 x-3chx-ch2 x) = 1+chx _

8ch2 (x/2)th(x/2) 4sh2 x(3+chx) shx(3+chx)

10.21.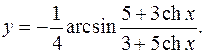

y'= -(3+5chx)(3shx(3+5chx)-5shx(5+3chx)) = 1

4(3+5chx)2 √(9+30chx+25ch2 x-25-30chx-9ch2 x)

10.22.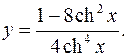

y'= -16ch5 xshx-4ch3 x(1-8ch2 x) = -4ch2 xshx-1+8ch2 x

4ch8 x ch5 x

10.23.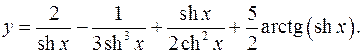

y'= -2/sh2 x+1/sh4 x+ch3 x-2chxsh2 x + 5chx = -2/sh2 x+1/sh4 x+1-sh2 x + 5_

2ch4 x 2+2sh2 x 2ch3 x 2chx

10.24.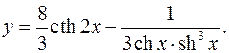

y'= -16 + sh4 x+3sh2 xch2 x = 1-4sh2 x

3sh2 2x 3ch2 xsh6 x ch2 xsh4 x

10.25.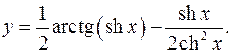

y'= chx _ 1-sh2 x = 1 _ 1-sh2 x

2+2sh2 x 2ch3 x 2ch2 x 2ch3 x

10.26.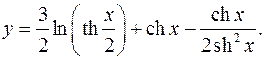

y'= 3 + shx – sh3 x-2shxch2 x = 1+sh2 x

4ch2 (x/2)th(x/2) 2sh4 x shx

10.27.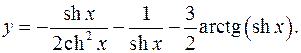

y'= 2chxsh2 x-ch3 x + 2shxchx _ 3chx = sh2 x-1 + 2chx _ 3 _

2ch4 x sh4 x 2+2sh2 x 2ch3 x sh3 x 2chx

10.28.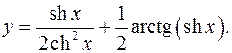

y'= ch3 x-2chxsh2 x + chx = 1 _

2ch4 x 2+2sh2 x ch3 x

10.29.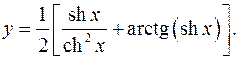

y'= ch3 x-2chxsh2 x + chx = 1 _

2ch4 x 2+2sh2 x ch3 x

10.30.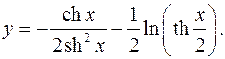

y'= 2ch2 xshx-sh3 x _ 1 = 1/sh3 x

2sh4 x 4ch2 (x/2)th(x/2)

10.31.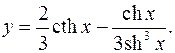

y'= -2 _ sh4 x-3ch2 xsh2 x = 1/sh4 x

3sh2 x 3sh6 x

Похожие работы