Уравнения поверхности и линии в пространстве

Уравнения поверхности и линии в пространстве

Основные понятия

Поверхность и ее уравнение

Поверхность в пространстве, как правило, можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О 1 есть геометрическое место всех точек пространства, находящихся от точки О1на расстоянии R.

Прямоугольная система координат О xyz в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел x , y и z – их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего координаты всех точек поверхности.

Уравнением данной поверхности в прямоугольной системе координат О xyz называется такое уравнение F ( x , y , z )=0 с тремя переменными x , y и z , которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности.

Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка М 1 ( x 1 ; y 1 ; z 1 ) на данной поверхности, достаточно подставить координаты точкиM1 в уравнение поверхности вместо переменных: если эти координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют – не лежит.

Уравнение сферы

Найдем уравнение сферы радиуса R c центром в точке О 1 ( x 0 ; y 0 ; z 0 ) . Согласно определению сферы расстояние любой ее точки М( x , y , z ) от центра О 1 ( x 0 ; y 0 ; z 0 ) равно радиусу R , т.е. О 1 М = R . Но О 1 М=| | , где =( x - x 0 ; y - y 0 ; z - z 0 ). Следовательно,

=R

или

Это и есть искомое уравнение сферы. Ему удовлетворяют координаты любой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.

Если центр сферы О 1 совпадает с началом координат, то уравнение сферы принимает вид

Если же дано уравнение вида F ( x ; y ; z ) =0, то оно, вообще говоря, определяет в пространстве некоторую поверхность.

Выражение «вообще говоря» означает, что в отдельных случаях уравнение F ( x ; y ; z ) =0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается».

Так, уравнению не удовлетворяют никакие действительные значения x , y , z . Уравнению удовлетворяют лишь координаты точек, лежащих на оси О x (из уравнения следует: y =0, z =0 , а x - любое число).

Итак, поверхность в пространстве можно задать геометрически и аналитически. Отсюда вытекает постановка двух основных задач:

1. Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.

2. Дано уравнение F ( x ; y ; z )=0. Исследовать форму поверхности, определяемой этим уравнением.

Уравнение линии в пространстве

Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 1) или как геометрическое место точек, общих двум поверхностям.

Если F 1 ( x ; y ; z )=0 и F 2 ( x ; y ; z )=0 – уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными:

Уравнения этой системы называются уравнениями линии в пространстве. Например, есть уравнения оси О x .

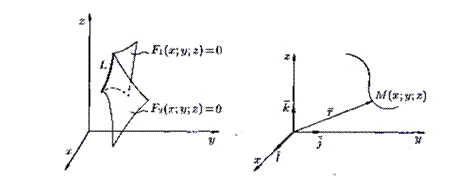Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 2). В этом случае ее задают векторным уравнением

(t)

Рис. 1 Рис. 2

или параметрическими уравнениями

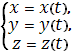
Проекцией вектора на оси координат.

Например, параметрические уравнения винтовой линии имеют вид

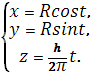
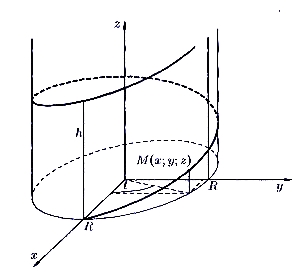Если точка М равномерно движется по образующей кругового цилиндра, а сам цилиндр равномерно вращается вокруг оси, то точка М описывает винтовую линию (см. рис. 3).

Рис. 3