Название: Уравнение Лапласа и гармонические функции

Вид работы: реферат

Рубрика: Математика

Размер файла: 160.18 Kb

Скачать файл: referat.me-218348.docx

Краткое описание работы: УРАВНЕНИЕ ЛАПЛАСА И ГАРМОНИЧЕСКИЕ ФУНКЦИИ Основные понятия Мы начнем с самого простого и важного из эллиптиче­ских уравнений, а именно с уравнения Лапласа.

Уравнение Лапласа и гармонические функции

УРАВНЕНИЕ ЛАПЛАСА И ГАРМОНИЧЕСКИЕ ФУНКЦИИ

Основные понятия

Мы начнем с самого простого и важного из эллиптиче­ских уравнений, а именно с уравнения Лапласа. Это урав­нение имеет вид

- ∆ u = f ( x )

Здесь f ( x ) — заданная функция. Если f ( x )≠0 , то уравне­ние (1) называется неоднородным уравнением Лапласа. При f ( x ) = 0 имеем однородное уравнение Лапласа

∆ u = 0

Неоднородное уравнение Лапласа часто называют уравнением Пуассона.

В более подробной записи уравнения Лапласа — неодно­родное и однородное — выглядят так:

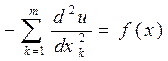
и соответственно

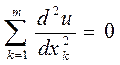
Рассмотрим некоторую замкнутую поверхность Г, не обязательно связную» и пусть Г ограничивает область Ω, конечную (рис. 1) или бесконечную (рис.2) В обоих слу­чаях предполагается» что сама поверхность Г конечна. Будемизучать поведение решений однородного уравнения Лапласа в подобных областях.

Функция и (х) называется гармонической в конечной области Ω, если она в этой области дважды непрерывно дифференцируема и удовлетворяет однородному уравнению Лапласа.

Будем говорить, что функция и(х) гармоническая в бес­конечной области Ω, если в каждой точке этой области, находящейся на конечном расстоянии or начала, u ( x ) дважды непрерывно дифференцируема, удовлетворяйi однородному уравнению Лапласа и па бесконечности имеет порядок

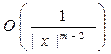,так что для достаточно больших |х| имеет место неравенство

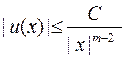
где т — размерность пространства, а С — некоторая постоян­ная. В случае двумерной области (т = 2) условие (3) озна­чает, что гармоническая в бесконечной области функция ограничена на бесконечности.

Подчеркнем, что определение гармонической функции отно­сится только к случаю открытой области (т. е. открытого связного множества); если говорят о функции, гармонической в замкнутой области, то под этим понимают, что данная функция гармонична в более широкой открытой области.

Заметим еще, что определение гармонической функции не накладывает никаких ограничений на поведение функции на границе области.

Пример 1: Если Ω — бесконечная область, то функция и (х) = 1 гармоническая только при т = 2. Если m > 2 , то в бесконечной области эта функции негармонична. Однако она гар­монична в любой конечной области при любом т.

Пример 2. В двумерной плоскости функция

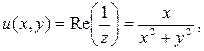
где z = х+ i у , гармонична в любой области, которая не содержит начала координат.

Пример 3. Функция z = x + iy , гармонична в круге | z | < R ( R — любое положительное число), разрезанном вдоль какого-либо из его радиусов.

Пример 4. Функция двух переменных и = х² + у² не являет­ся гармонической ни в какой области, так как она не удовлетво­ряет однородному уравнению Лапласа

∆( x ² + y ² ) = 4 ≠ 0.

Пример 5. Функция u = x ² - y ² гармонична в любой конеч­ной области.

На двумерной плоскости конформное преобразование не меняет однородного уравнения Лапласа. В случае любого т это не так, но все же существует преобразование, которое перево­дит любую гармоническую функцию в гармоническую же. Это пре образование Кельвина, которое переводит точку

х (х_и х₂ , ... , х_т ) в точку х’ (х’_и х’₂ , ... , х’_т ) , симметричную с точкой х относительно сферы данного радиуса R с центром в начале координат, а дан ную функцию и (х) переводит в функцию

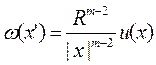
Напомним, что точки х и х' называются симметричными относительно названной выше сферы, если они лежат на одном луче, исходящем из начала, и если | х | • | х'| = R ² . Декартовы коор­динаты симметричных точек связаны соотношением

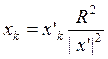
Простой, хотя и довольно громоздкий подсчет приводит к соотношению

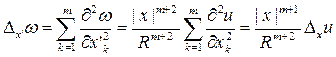
поэтому если то .