Название: Автоколебательные системы
Вид работы: реферат
Рубрика: Математика
Размер файла: 43.91 Kb
Скачать файл: referat.me-216722.docx
Краткое описание работы: Примеры автоколебательных систем.
Автоколебательные системы
Под автоколебаниями понимают колебательный процесс в диссипативных системах (т.е. в системах с потерями задействованной в процессе энергии - на трение, выделение тепла), характеристики которого - амплитуда колебаний, их форма, период и частота (в более общем случае - спектр) определяются самой системой и не зависят от изменения начальных условий. Образ автоколебаний в фазовом пространстве - аттрактор - фазовая траектория или множество траекторий, к которому притягиваются все близлежащие траектории. Аттрактор, отвечающий периодическим автоколебаниям, есть замкнутая фазовая траектория - предельный цикл.
Автоколебательные системы
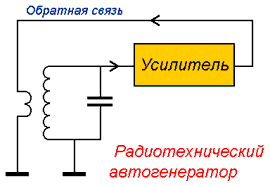
Схема содержит колебательный контур. При наличии в нем колебаний переменное напряжение поступает на вход усилителя, а усиленный сигнал через цепь обратной связи "подталкивает" в нужной фазе колебания в контуре -без этого они были бы затухающими. При правильном знаке коэффициента передачи цепи обратной связи, начиная с некоторой величины коэффициента усиления, возникают автоколебания - колебательный процесс, амплитуда и частота которого определяются самой системой и не зависят от начальных условий.
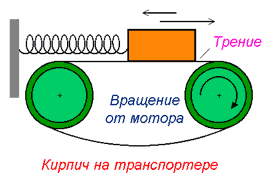
Механическая автоколебательная система, условием функционирования которой служит наличие падающего участка в зависимости силы трения кирпича о ленту транспортера от скорости.

Самая древняя автоколебательная система - маятниковые часы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается, но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
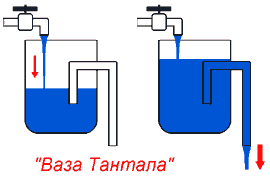
Тантал - наказанный богами персонаж древнегреческого мифа, который не мог напиться, стоя в воде: когда он наклонялся, вода уходила.
Система работает так: сначала вода наполняет резервуар, отводная трубка наполнена воздухом, и вода не вытекает. Когда вода покроет трубку, она начинает вытекать. При этом действует эффект сифона - вытекание прекратится только тогда, когда уровень воды в резервуаре упадет до нижнего обреза трубки, и в нее попадет воздух. Скорость вытекания через трубку должна быть больше, чем скорость поступления воды в резервуар из крана.
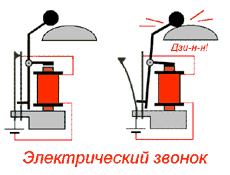
Электромеханическая автоколебательная система. Когда электрическая цепь замкнута, электромагнит притягивает железную деталь с молоточком, ударяющим по звонку, и разрывает цепь. После этого система возвращается в исходное положение, и процесс повторяется.
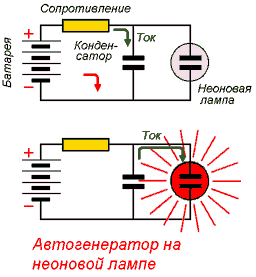
Неоновая лампочка не зажигается, пока напряжение на ней меньше некоторой пороговой величины. На этом этапе ток от батареи течет через сопротивление, конденсатор постепенно заряжается, напряжение на пластинах растет. Когда оно достигает порогового, лампа вспыхивает, и конденсатор быстро разряжается через нее. После погасания лампы процесс начинается снова.

Поток воздуха, скорость которого больше некоторой критической величины, вызывает колебания - полоскание флага на ветру.
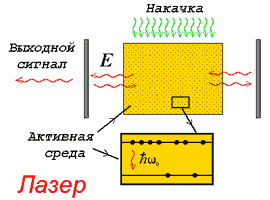
Тем или иным способом, например, посредством облечения некогерентным светом от мощной лампы (накачка), в активной среде создается инверсная заселенность - большая часть атомов располагается на верхнем квантовом энергетическом уровне. Если в резонаторе, образованном двумя зеркалами, присутствует излучение, и частота отвечает частоте перехода между уровнями, атомы переходят с верхнего уровня на нижний. При этом они испускают индуцированное излучение, благодаря которому потери в резонаторе и выходная мощность компенсируются, колебания в резонаторе не затухают, пока действует накачка.
Похожие работы
-
Математическая модель системы в переменных пространства состояний
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СИСТЕМ В ПЕРЕМЕННЫХ ПРОСТРАНСТВА СОСТОЯНИЙ ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ Математическая модель системы в переменных пространства состояний имеет вид
-
Определители
Муниципальное образовательное учреждение – гимназия № 47 Реферат по математике ученицы 8 г класса Годуновой Екатерины г.Екатеринбург, 2000г. Введение
-
Поле. Примеры полей. Свойства полей. Поле рациональных чисел
Рассматривается определение поля, примеры и простейшие свойства полей, определения подполя, простого поля и поля рациональных чисел.
-
Основные правила дифференцирования
Производные основных элементарных функций. Логарифмическое дифференцирование. Показательно-степенная функция и ее дифференцирование. Производная обратных функций. Связь между дифференциалом и производной. Теорема об инвариантности дифференциала.
-
Метод Гаусса
Методические рекомендации по выполнению заданий методом гауса. Примеры выполнения заданий.
-
Экзаменационные билеты по теоретической механике
Билеты по разделу "Динамика".
-
Физические ограничения существования планетарных систем
Принятая на веру, широко распространенная точка зрения: что составляющие сил гравитации, сами являются именно силами притяжения, не соответствует Законам Сохранения Энергии, в силу чего является физически неверной.
-
Метод Крамера
Министерство рыбного хозяйства Владивостокский морской колледж ТЕМА: “ Системы 2-х , 3-х линейных уравнений. Правило Крамера. ” г. Владивосток
-
Интересные примеры в метрических пространствах
Интересные примеры в метрических пространствах: 1. В n-мерном евклидовом пространстве полная ограниченность совпадает с обычной ограниченностью, то есть с возможностью заключить данное множество в достаточно большой куб. Действительно, если такой куб разбить на кубики с ребром , то вершины этих кубиков будут образовывать конечную
-
Системы 2-х, 3-х линейных уравнений, правило Крамера
Краткая теория. Методические рекомендации по выполнению заданий. Примеры выполнения заданий.