Referat.me
/ / Системы 2-х, 3-х линейных уравнений, правило Крамера

Название: Системы 2-х, 3-х линейных уравнений, правило Крамера

Вид работы: доклад

Рубрика: Математика

Размер файла: 63.61 Kb

Скачать файл: referat.me-215061.docx

Краткое описание работы: Краткая теория. Методические рекомендации по выполнению заданий. Примеры выполнения заданий.

Системы 2-х, 3-х линейных уравнений, правило Крамера

Системы 2-х , 3-х линейных уравнений, правило Крамера

ОГЛАВЛЕНИЕ.

1.Краткая теория .

2. Методические рекомендации по выполнению заданий.

3.Примеры выполнения заданий.

4.Варианты заданий.

5.Список литературы.

1. КРАТКАЯ ТЕОРИЯ .

Пусть дана система линейных уравнений

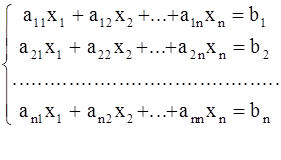(1)

Коэффициенты a11 ,12 ,..., a1n , ... , an1 , b2 , ... , bn считаются заданными .

Вектор -строка íx1 , x2 , ... , xn ý - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.

Определитель n-го порядка D=çAê=ça ij ç, составленный из коэффициентов при неизвестных , называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи.

a). Если D¹0, то система (1) имеет единственное решение, которое может быть найдено по формулам Крамера : x1 =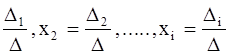, где

определитель n-го порядка Di ( i=1,2,...,n) получается из определителя системы путем замены i-го столбца свободными членами b1 , b2 ,..., bn .

б). Если D=0 , то система (1) либо имеет бесконечное множество решений , либо несовместна ,т.е. решений нет.

2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.

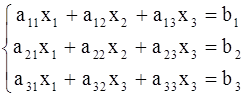(2).

1. В данной системе составим определитель 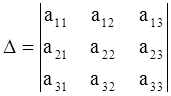и вычислим.

2. Составить и вычислить следующие определители :

.

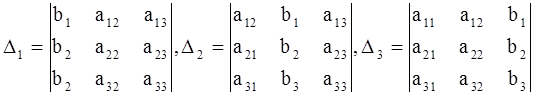3. Воспользоваться формулами Крамера.

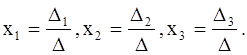
3. ПРИМЕРЫ.

1. .

.

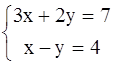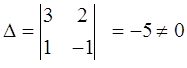
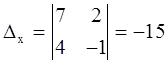
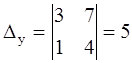
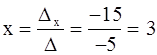
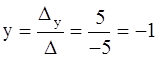Проверка:

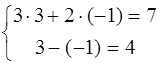Ответ: ( 3 ; -1 ).

2.

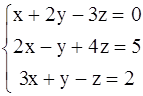
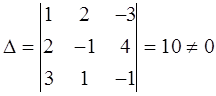
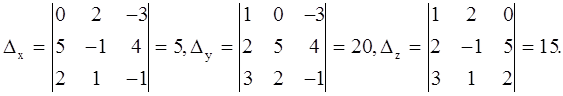
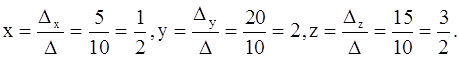
Проверка:

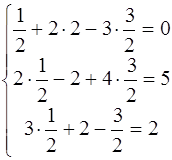
Ответ: x=0,5 ; y=2 ; z=1,5 .

4. ВАРИАНТЫ ЗАДАНИЙ.

ВАРИАНТ 1.

Решить системы:

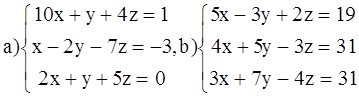
ВАРИАНТ 2.

Решить системы:

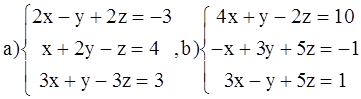
ВАРИАНТ 3.

Решить системы:

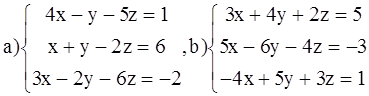
ВАРИАНТ 4.

Решить системы:

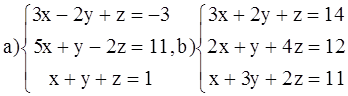
ВАРИАНТ 5.

Решить системы:

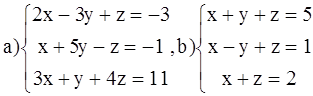
ВАРИАНТ 6.

Решить системы:

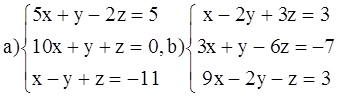
ВАРИАНТ 7.

Решить системы:

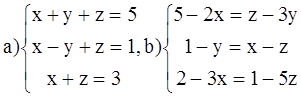
ВАРИАНТ 8.

Решить системы:

Литература

1. Г.И. КРУЧКОВИЧ. “Сборник задач по курсу высшей математике”, М. “Высшая школа”, 1973 год.

2. В.С. ШИПАЧЕВ. “Высшая математика”, М. “Высшая школа”, 1985 год.

Похожие работы

  • Системы линейных уравнений и неравенств

    Основные понятия теории систем уравнений. Метод Гаусса — метод последовательного исключения переменных. Формулы Крамера. Решение систем линейных уравнений методом обратной матрицы. Теорема Кронекер–Капелли. Совместность систем однородных уравнений.

  • Алгебра матриц. Системы линейных уравнений

    Выполнение действий над матрицами. Определение обратной матрицы. Решение матричных уравнений и системы уравнений матричным способом, используя алгебраические дополнения. Исследование и решение системы линейных уравнений методом Крамера и Гаусса.

  • Метод Гаусса

    Методические рекомендации по выполнению заданий методом гауса. Примеры выполнения заданий.

  • Метод Крамера

    Министерство рыбного хозяйства Владивостокский морской колледж ТЕМА: “ Системы 2-х , 3-х линейных уравнений. Правило Крамера. ” г. Владивосток

  • Применение непрерывности и производной 11 класс

    Лабораторная работа №1 Характеристики тестовых заданий План: Составление матрицы, приведение к треугольному виду, анализ неверных профилей, подсчет мер центральной тенденции, мер изменчивости, мер симметрии и островершинности кривой распределения.

  • Итерационные методы решения системы линейных алгебраических уравнений

    Кафедра: Автоматика и информационные технологии "ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ" Екатеринбург 2006 РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ПРОСТОЙ ИТЕРАЦИИ

  • Задачи по Математике

    ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ Задачи № 1-10. Решить систему линейных алгебраических уравнений тремя способами: 1) методом Крамера, 2) с помощью обратной матрицы, 3) методом Гаусса.

  • Аппроксимация функции методом наименьших квадратов

    Постановка задачи аппроксимации методом наименьших квадратов, выбор аппроксимирующей функции. Общая методика решения данной задачи. Рекомендации по выбору формы записи систем линейных алгебраических уравнений. Решение систем методом обратной матрицы.

  • Исследования и теории Габриеля Крамера

    Преподавательская работа швейцарского математика Габриэля Крамера, введение в анализ алгебраических кривых. Система произвольного количества линейных уравнений с квадратной матрицей Крамера. Классификация и порядок математических и алгебраических кривых.

  • Системы линейных уравнений

    Критерий совместности. Метод Гаусса. Формулы Крамера. Матричный метод.