Название: Метод Гаусса
Вид работы: доклад
Рубрика: Математика
Размер файла: 55.4 Kb
Скачать файл: referat.me-217496.docx
Краткое описание работы: Методические рекомендации по выполнению заданий методом гауса. Примеры выполнения заданий.
Метод Гаусса
ОГЛАВЛЕНИЕ.
1. Историческая справка
2. Краткая теория
3. Методические рекомендации по выполнению заданий.
4. Примеры выполнения заданий.
1. Историческая справка
ГАУСС (Gaus ) Карл Фридрих (1777-1855), нем. математик, ин. ч.-к. (1802) и ин. поч. ч. (1824) Петерб. АН. Для творчества Г. характерна органич. связь между теоретич. и прикладной матедатикой, широта проблематики. Тр. Г. оказали большое влияние на развитие алгебры (доказательство осн. теоремы алгебры), теории чисел (квадратичные вычеты), дифференц. геометрии (внутр. геометрия поверхностей), матем. физики (принцип Г.), теории электричества и магнетизма, геодезии (разработка метода наименьших квадратов) и мн. разделов астрономии.
2. КРАТКАЯ ТЕОРИЯ .
Пусть дана система линейных уравнений
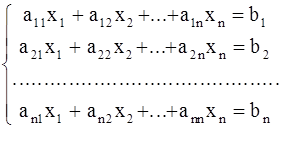 (1)
(1)
Коэффициенты a11 ,12 ,..., a1n , ... , an1 , b2 , ... , bn считаются заданными .
Вектор -строка íx1 , x2 , ... , xn ý - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D=çAê=ça ij ç, составленный из коэффициентов при неизвестных , называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи.
a). Если D¹0, то система (1) имеет единственное решение, которое может быть найдено методом ГАУССА .
б). Если D=0 , то система (1) либо имеет бесконечное множество решений , либо несовместна ,т.е. решений нет.
2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
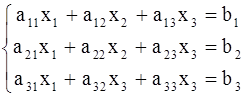 (2).
(2).
Метод Гаусса решения системы (2) состоит в следующем:
Разделим все члены первого уравнения на ![]() , а затем ,умножив полученное уравнение на
, а затем ,умножив полученное уравнение на ![]() , вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное
, вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное ![]() будет исключено ,и получиться система вида:
будет исключено ,и получиться система вида:
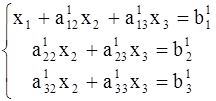 (3)
(3)
Теперь разделим второе уравнение системы (3) на![]() , умножим полученное уравнение на
, умножим полученное уравнение на ![]() и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное
и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное ![]() будет исключено и получиться система треугольного вида :
будет исключено и получиться система треугольного вида :
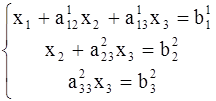 (4)
(4)
Из последнего уравнения системы (4) находим ![]() ,подставляя найденное
,подставляя найденное
подставляя найденное значение в первое уравнение , находим ![]() .
.
3. ПРИМЕР.
Методом Гаусса решить систему:
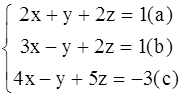
Решение: Разделив уравнение (а) на 2 , получим систему 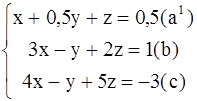
Вычтем из уравнения (b) уравнение ![]() , умноженное на 3, а из уравнения (c) -
, умноженное на 3, а из уравнения (c) -
уравнение ![]() , умноженное на 4.
, умноженное на 4.
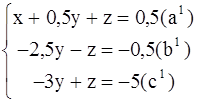
Разделив уравнение![]() (
(![]() ) на -2,5 , получим :
) на -2,5 , получим : 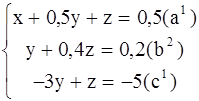
Вычтем из уравнения (![]() ) уравнение
) уравнение ![]() , умноженное на -3:
, умноженное на -3:
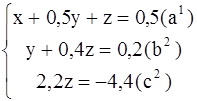
Из уравнения ![]() находим Z=-2; подставив это значение в уравнение
находим Z=-2; подставив это значение в уравнение ![]() , получим Y=0,2-0,4Z=0,2-0,4(-2)=1; наконец , подставив значение Z=-2 и Y=1 в уравнение(a1
) , находим X=0,5-0,5Y-Z=0,5-0,5 1 - (-2)=2. Итак, получаем ответ X=2, Y=1, Z=-2 .
, получим Y=0,2-0,4Z=0,2-0,4(-2)=1; наконец , подставив значение Z=-2 и Y=1 в уравнение(a1
) , находим X=0,5-0,5Y-Z=0,5-0,5 1 - (-2)=2. Итак, получаем ответ X=2, Y=1, Z=-2 .
Проверка:
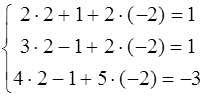
Похожие работы
-
Преобразование графиков функции
Тема: « Преобразование графиков функции Цели: 1) Систематизировать приемы построения графиков. 2) Показать их применение при построении: а) графиков сложных функций;
-
Методические материалы по учебной дисциплине "Высшая математика" для студентов I курса заочной формы обучения
Элементы линейной алгебры. Элементы аналитической геометрии и векторной алгебры. Введение в математический анализ. Дифференциальное исчисление функций одной переменной. Дифференциальное исчисление функций нескольких независимых переменных. Интеграл.
-
Метод Крамера
Министерство рыбного хозяйства Владивостокский морской колледж ТЕМА: “ Системы 2-х , 3-х линейных уравнений. Правило Крамера. ” г. Владивосток
-
Применение непрерывности и производной 11 класс
Лабораторная работа №1 Характеристики тестовых заданий План: Составление матрицы, приведение к треугольному виду, анализ неверных профилей, подсчет мер центральной тенденции, мер изменчивости, мер симметрии и островершинности кривой распределения.
-
Обчислення матричних задач
МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ Бердичівський політехнічний коледж Контрольна робота з дисципліни “Числові методи” Виконав: студент групи Пзс-503 Лифар Сергій Олександрович
-
Решения к Сборнику заданий по высшей математике Кузнецова Л.А. - 2. Дифференцирование. Зад.19
Задача 19 . Найти производную второго порядка от функции, заданной параметрически. 19.1. x'= -2sin2t= -4sintcost y'= 4sint/cos3t y''xx= 4sint = -1 _ 16sin2tcos5t 4sintcos5t
-
Решения к Сборнику заданий по высшей математике Кузнецова Л.А. - 2. Дифференцирование. Зад.17
Задача 17 . Найти производную -го порядка. 17.1. y'= eαx+αxeαx y''= 2αeαx+α2xeαx y'''= 3α2eαx+α3xeαx
-
Итерационные методы решения системы линейных алгебраических уравнений
Кафедра: Автоматика и информационные технологии "ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ" Екатеринбург 2006 РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ПРОСТОЙ ИТЕРАЦИИ
-
Аппроксимация функции методом наименьших квадратов
Постановка задачи аппроксимации методом наименьших квадратов, выбор аппроксимирующей функции. Общая методика решения данной задачи. Рекомендации по выбору формы записи систем линейных алгебраических уравнений. Решение систем методом обратной матрицы.
-
Системы 2-х, 3-х линейных уравнений, правило Крамера
Краткая теория. Методические рекомендации по выполнению заданий. Примеры выполнения заданий.