Название: Атомические разложения функций в пространстве Харди
Вид работы: реферат
Рубрика: Математика
Размер файла: 792.87 Kb
Скачать файл: referat.me-216821.docx
Краткое описание работы: Міністерство Освіти України Одеський державний університет ім. І.І.Мечнікова Інститут математики, економіки та механіки Атомічні розкладення функцій
Атомические разложения функций в пространстве Харди
Міністерство Освіти України
Одеський державний університет
ім. І.І.Мечнікова
Інститут математики, економіки та механіки
Атомічні розкладення функцій
у просторі Харді
Дипломна робота
студентки V курсу
факультету математики
Семенцовой В.А.
Науковий керівник
Вартанян Г.М.
Одеса - 2000
Содержание
Введение.................................................................................... 3
Глава I. Основные сведения об интеграле Пуассона и
пространствах ![]() ,
, ![]() и
и ![]() ................................. 8
................................. 8
§I.1. Интеграл Пуассона..................................................... 8
§I.2. Пространства ![]() ....................................................... 12
....................................................... 12
§I.3. Пространства ![]() и
и ![]() ......................................... 17
......................................... 17
§I.4. Произведение Бляшке, нетангенциальная
максимальная функция............................................... 22
Глава II. Атомические разложения функции в пространстве
![]() , пространство ВМО........................................ 26
, пространство ВМО........................................ 26
§II.1. Пространство ![]() , критерий принадлежности
, критерий принадлежности
функции из ![]() пространству
пространству ![]() ....................... 26
....................... 26
§II.2. Линейные ограниченные функционалы на ![]() ,
,
двойственность ![]() и ВМО.................................. 32
и ВМО.................................. 32
Литература.................................................................................. 37
Введение.
Целью настоящей работы является изучение основных понятий и результатов, полученных в области пространств Харди, которая не изучалась в рамках университетского курса. В работе прослежена взаимосвязь между следующими понятиями : интеграл Пуассона, пространства ![]() ,
, ![]() ,
, ![]() и
и ![]() , раскрыта суть и структура этих объектов. Описание указанных понятий вводится именно в такой последовательности , так как определение каждого последующего объекта дается на основе понятий, расположенных левее в выше перечисленном ряду объектов.
, раскрыта суть и структура этих объектов. Описание указанных понятий вводится именно в такой последовательности , так как определение каждого последующего объекта дается на основе понятий, расположенных левее в выше перечисленном ряду объектов.
Работа состоит из двух глав, каждая из которых делится на параграфы. В первой главе изучены свойства пространств ![]() ,
, ![]() ,
, ![]() , а во второй мы доказываем коитерий принадлежности функции из
, а во второй мы доказываем коитерий принадлежности функции из ![]() пространству
пространству ![]() и двойственность пространств
и двойственность пространств ![]() и
и ![]() .
.
В работе мы рассматриваем случай ![]() периодических функций. Используемые обозначения имеют следующий смысл:
периодических функций. Используемые обозначения имеют следующий смысл:
![]() - пространство
- пространство ![]() периодических, непрерывных на
периодических, непрерывных на ![]() функций;
функций;
![]() - пространство
- пространство ![]() периодических, бесконечно дифференцируемых на
периодических, бесконечно дифференцируемых на ![]() функций;
функций;
![]() - пространство
- пространство ![]() периодических, суммируемых в степени р на
периодических, суммируемых в степени р на ![]() функций, т.е.для которых
функций, т.е.для которых 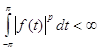 ,
, ![]() ;
;
![]() - пространство
- пространство ![]() периодических ограниченных на
периодических ограниченных на ![]() функций;
функций;
![]() - носитель функции
- носитель функции ![]() .
.
В §I.1.вводится понятие интеграла Пуассона: интегралом Пуассона суммируемой на [-p,p] 2p-периодической комплекснозначной функции ![]() называется функция
называется функция
¦r
( x ) = 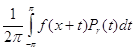 ,
,
где ![]() , t Î [ -p, p ] - ядро Пуассона.
, t Î [ -p, p ] - ядро Пуассона.
Здесь мы доказываем следующие свойства ядра Пуассона, которые мы неоднократно будем использовать в ряде доказательств:
а) ![]() ;
;
б) 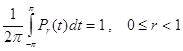 ;
;
в) для любого d>0
![]()
Основной целью данного параграфа являются две теоремы о поведении интеграла Пуассона ![]() при
при ![]() :
:
Теорема 1.
Для произвольной (комплекснозначной) функции ![]() ( -p, p ) , 1 £ p < ¥ , имеет место равенство
( -p, p ) , 1 £ p < ¥ , имеет место равенство![]()
![]() ;
;
если же ¦ (x) непрерывна на [ -p, p ] и ¦ (-p) = ¦ (p) , то
![]() .
.
Теорема 2 (Фату).
Пусть ![]() - комплекснозначная функция из
- комплекснозначная функция из ![]() . Тогда
. Тогда
![]() для п.в.
для п.в. ![]() .
.
В этом параграфе мы обращались к следующим понятиям:
Определение1. Функция ![]() называется аналитической в точке
называется аналитической в точке ![]() , если она дифференцируема в этой точке и в некоторой ее окрестности. Говорят, что функция
, если она дифференцируема в этой точке и в некоторой ее окрестности. Говорят, что функция ![]() аналитична на некотором множестве,если она аналитична в каждой точке этого множества.
аналитична на некотором множестве,если она аналитична в каждой точке этого множества.
Определение2. Действительная функция двух действительных переменных ![]() называется гармонической в области
называется гармонической в области ![]() , если
, если ![]() и удовлетворяет уравнению Лапласа:
и удовлетворяет уравнению Лапласа:
![]() .
.
Определение3. Две гармонические функции ![]() и
и ![]() , связанные условиями Коши-Римана :
, связанные условиями Коши-Римана : ![]() ,
, ![]() , называются гармонически сопряженными функциями.
, называются гармонически сопряженными функциями.
Определение4. Под нормой пространства ![]() понимается
понимается
![]() ,
, ![]() .
.
Определение5. Под нормой пространства ![]() понимается
понимается
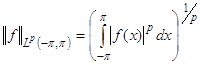 ,
, ![]() .
.
Определение6. Пусть ![]() ( или
( или ![]() ,
,![]() ). Модуль непрерывности ( соответственно интегральный модуль непрерывности) функции
). Модуль непрерывности ( соответственно интегральный модуль непрерывности) функции ![]() определяется равенством
определяется равенством
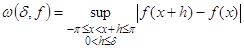 ,
, ![]() .
.
(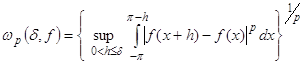 ,
, ![]() ).
).
Определение7. Последовательность ![]() функций, определенных на множестве Х с заданной на нем мерой, называется сходящейся почти всюду к функции
функций, определенных на множестве Х с заданной на нем мерой, называется сходящейся почти всюду к функции ![]() , если
, если ![]() для почти всех
для почти всех ![]() , т.е. множество тех точек
, т.е. множество тех точек ![]() , в которых данное соотношение не выполняется, имеет меру нуль.
, в которых данное соотношение не выполняется, имеет меру нуль.
В §I.2 мы рассматриваем пространства ![]() - это совокупность аналитических в единичном круге функций F (z) , для которых конечна норма
- это совокупность аналитических в единичном круге функций F (z) , для которых конечна норма
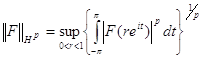 .
.
Основным результатом этого параграфа является теорема о том, что любую функцию ![]() (
(![]() ) можно предсавить в виде
) можно предсавить в виде
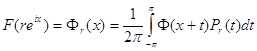 ,
, ![]() ,
, ![]() ,
,
где ![]() для п.в.
для п.в. ![]() , при этом
, при этом
![]()
![]() ;
;
![]()
![]() .
.
Использованные в данном параграфе понятия мы принимаем в следующих определениях:
Определение8. Говорят, что действительная функция ![]() , заданная на отрезке [a,b], имеет ограниченную вариацию, если существует такая постоянная
, заданная на отрезке [a,b], имеет ограниченную вариацию, если существует такая постоянная ![]() , что каково бы ни было разбиение отрезка [a,b] точками
, что каково бы ни было разбиение отрезка [a,b] точками ![]() выполнено неравенство
выполнено неравенство ![]() .
.
Определение9. Действительная функция ![]() , заданная на отрезке [a,b], называется абсолютно непрерывной на [a,b], если для любого
, заданная на отрезке [a,b], называется абсолютно непрерывной на [a,b], если для любого ![]() найдется число
найдется число ![]() такое, что какова бы ни была система попарно непересекающихся интервалов
такое, что какова бы ни была система попарно непересекающихся интервалов ![]() ,
, ![]() с суммой длин, меньшей
с суммой длин, меньшей ![]() :
: ![]() , выполняется неравенство
, выполняется неравенство ![]() .
.
В третьем параграфе первой главы мы переходим к рассмотрению пространств ![]() и
и ![]() . Пространство
. Пространство ![]() (
(![]() ) представляет собой совокупность тех функций
) представляет собой совокупность тех функций ![]() ,
, ![]() , которые являются граничными значениями функций (действительных частей функций) из
, которые являются граничными значениями функций (действительных частей функций) из![]() , т.е. представимы в виде
, т.е. представимы в виде ![]() (
(![]() ). Здесь мы получаем следующие результаты: при
). Здесь мы получаем следующие результаты: при ![]() пространство
пространство ![]() совпадает с
совпадает с ![]() , а при р=1
, а при р=1 ![]() уже, чем
уже, чем ![]() , и состоит из функций
, и состоит из функций ![]() , для которых и
, для которых и ![]() .
.
В §I.4 мы вводим понятие произведения Бляшке функции ![]() , аналитической в круге
, аналитической в круге ![]() с нулями
с нулями ![]() ,
, ![]() (
(![]() ) с учетом их кратности:
) с учетом их кратности:
![]() ,
,
где ![]() - кратность нуля функции
- кратность нуля функции ![]() при
при ![]() .
.
Здесь доказывается, что каждая функция ![]() представима в виде
представима в виде
![]() , где
, где ![]() не имеет нулей в круге
не имеет нулей в круге ![]() и
и ![]() ,
, ![]() ,а
,а ![]() - произведение Бляшке функции
- произведение Бляшке функции ![]() .
.
Затем мы рассматриваем понятие нетангенциальной максимальной функции . Пусть ![]() ,
, ![]() , - произвольное число. Обозначим через
, - произвольное число. Обозначим через ![]() ,
, ![]() , область, ограниченную двумя касательными, проведенными из точки
, область, ограниченную двумя касательными, проведенными из точки ![]() к окружности
к окружности ![]() , и наибольшей из дуг окружности, заключенных между точками касания ( при
, и наибольшей из дуг окружности, заключенных между точками касания ( при ![]()
![]() вырождается в радиус единичного круга). Для
вырождается в радиус единичного круга). Для ![]() положим
положим
![]() ,
, ![]() ,
,
где ![]() - интеграл Пуассона функции
- интеграл Пуассона функции ![]() . Функция
. Функция ![]() называется нетангенциальной максимальной функцией для
называется нетангенциальной максимальной функцией для ![]() .
.
Тут же мы доказываем теорему об оценке ![]() : если
: если ![]() (
(![]() ),
), ![]() , то
, то ![]() и
и ![]() .
.
Первые результаты о максимальных функциях были получены в 1930 году Харди и Литтлвудом.
Во второй главе два параграфа.
В §II.1 рассматривается пространство ![]() . Как ранее отмечалось, оно уже, чем
. Как ранее отмечалось, оно уже, чем ![]() . Поэтому в данном параграфе большой интерес представляет теорема - критерий принадлежности функции пространству
. Поэтому в данном параграфе большой интерес представляет теорема - критерий принадлежности функции пространству ![]() . Здесь вводится понятие атома: действительная функция
. Здесь вводится понятие атома: действительная функция ![]() называется атомом, если существует обобщенный интервал
называется атомом, если существует обобщенный интервал ![]() такой, что
такой, что
а) ![]() ; б)
; б) 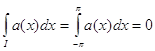 ; в)
; в) ![]() .
.
Атомом назовем также функцию ![]() ,
, ![]() . Под обобщенным интервалом понимается либо интервал из
. Под обобщенным интервалом понимается либо интервал из ![]() , либо множество вида
, либо множество вида![]()
![]() (
(![]() ).
).
Данный параграф посвящен аналогу теоремы, доказанной в 1974 году Р.Койфманом о том, что функция ![]() тогда и только тогда, когда функция
тогда и только тогда, когда функция ![]() допускает представление в виде
допускает представление в виде
![]() ,
, ![]() , где
, где ![]() ,
, ![]() , - атомы. (*)
, - атомы. (*)
При этом ![]() , где inf берется по всем разложениям вида (*) функции
, где inf берется по всем разложениям вида (*) функции ![]() , а с и С
, а с и С ![]() - абсолютные константы.
- абсолютные константы.
Роль атомических разложений заключается в том, что они в ряде случаев позволяют свести вывод глубоких фактов к относительно простым действиям с атомами.
В частночти, из атомического разложения функций, принадлежащих пространству ![]() , легко вытекает полученный в 1971 году Ч.Фефферманом результат о двойственности пространств
, легко вытекает полученный в 1971 году Ч.Фефферманом результат о двойственности пространств ![]() и
и ![]() . Доказательству этого факта и посвящен второй параграф данной главы. Сперва мы вводим определение
. Доказательству этого факта и посвящен второй параграф данной главы. Сперва мы вводим определение ![]() : пространство ВМО есть совокупность всех функций
: пространство ВМО есть совокупность всех функций ![]() , удовлетворяющих условию
, удовлетворяющих условию
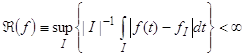 , (91)
, (91)
где ![]() , а sup берется по всем обобщенным интервалам
, а sup берется по всем обобщенным интервалам ![]() . А затем доказываем теорему о том, что
. А затем доказываем теорему о том, что ![]() .
.
Глава I.
Основные сведения об интеграле Пуассона и
пространствах
![]() ,
, ![]() и
и ![]()
§I.1.Интеграл Пуассона.
Пусть ¦(x ) , g (x ) , x ÎR1 –суммируемые на [-p, p] , 2p- периодические, комплекснозначные функции. Через f*g(x) будем обозначать свертку
![]() f*g(x)
=
f*g(x)
=![]()
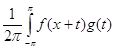 dt
dt![]()
![]()
![]()
![]()
Из теоремы Фубини следует, что свертка суммируемых функций также суммируема на [-p,p] и
cn ( f*g ) = cn ( f )× c-n ( g ) , n = 0, ±1 , ±2 , ... ( 1 )
где { cn ( f )} - коэффициенты Фурье функции f ( x ) :
cn
(f)= 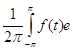 -i n t
dt
, n = 0, ±1, ±2,¼
-i n t
dt
, n = 0, ±1, ±2,¼
Пусть ¦ Î L1 (-p, p ) . Рассмотрим при 0 £ r < 1 функцию
¦r
( x ) = ![]() n
( f ) r| n |
ei n x
, x Î [ -p, p ] . ( 2 )
n
( f ) r| n |
ei n x
, x Î [ -p, p ] . ( 2 )
Так как ![]() для любых x Î [ -p, p ], n = 0, ±1, ±2,¼, а ряд
для любых x Î [ -p, p ], n = 0, ±1, ±2,¼, а ряд ![]() сходится (так как согласно теореме Мерсера [4] коэффициенты Фурье любой суммируемой функции по ортогональной системе ограниченных в совокупности функций
сходится (так как согласно теореме Мерсера [4] коэффициенты Фурье любой суммируемой функции по ортогональной системе ограниченных в совокупности функций ![]() стремятся к нулю при
стремятся к нулю при ![]() ), то по признаку Вейерштрасса ряд в правой части равенства (2) сходится равномерно по х для любого фиксированного r , 0 £ r < 1 . Коэффициенты Фурье функции ¦r
(х) равны cn
( fr
) = cn
(f)× r| n |
, n = 0 , ±1, ±2, ¼ , а это значит, что ¦r
( x ) можно представить в виде свертки :
), то по признаку Вейерштрасса ряд в правой части равенства (2) сходится равномерно по х для любого фиксированного r , 0 £ r < 1 . Коэффициенты Фурье функции ¦r
(х) равны cn
( fr
) = cn
(f)× r| n |
, n = 0 , ±1, ±2, ¼ , а это значит, что ¦r
( x ) можно представить в виде свертки :![]()
¦r
( x ) = 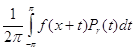 , ( 3 )
, ( 3 )
где
![]() , t Î [ -p, p ] . ( 4 )
, t Î [ -p, p ] . ( 4 )
Функция двух переменных Рr (t) , 0 £ r <1 , t Î [ -p, p ] , называется ядром Пуассона , а интеграл (3) - интегралом Пуассона .
![]()
![]()
![]()
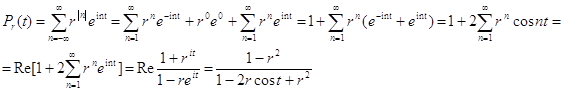
![]()
Следовательно,
Pr
( t ) = ![]() , 0 £ r < 1 , t Î [ -p, p] . ( 5 )
, 0 £ r < 1 , t Î [ -p, p] . ( 5 )
Если ¦Î L1 ( -p, p ) - действительная функция , то , учитывая , что
c-n
( f ) = ![]() , n = 0, ±1, ±2,¼, из соотношения (2) мы получим :
, n = 0, ±1, ±2,¼, из соотношения (2) мы получим :
fr
( x ) = ![]()
=![]() , ( 6 )
, ( 6 )
где
F ( z ) = c0
( f ) + 2 ![]() ( z = reix
) ( 7 )
( z = reix
) ( 7 )
- аналитическая в единичном круге функция как сумма равномерно сходящегося по х ряда [5]. Равенство (6) показывает, что для любой действительной функции ¦Î L1 ( -p, p ) интегралом Пуассона (3) определяется гармоническая в единичном круге функция
u ( z ) = ¦r (eix ) , z = reix , 0 £ r <1 , x Î [ -p, p ] .
При этом гармонически сопряженная с u (z) функция v (z) c v (0) = 0 задается формулой
v (z) = Im F (z) = ![]() . ( 8 )
. ( 8 )
Утверждение1.
Пусть u (z) - гармоническая ( или аналитическая ) в круге | z | < 1+e ( e>0 ) функция и ¦ (x) = u (eix ) , xÎ[ -p, p ] . Тогда
u (z) = 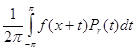 ( z = reix
, | z | < 1 ) ( 10 )
( z = reix
, | z | < 1 ) ( 10 )
Так как ядро Пуассона Pr (t) - действительная функция, то равенство (10) достаточно проверить в случае, когда u (z) - аналитическая функция:
![]() =
=![]() , | z | < 1+ e .
, | z | < 1+ e .
Но тогда коэффициенты Фурье функции ![]() связаны с коэффициентами Фурье функции
связаны с коэффициентами Фурье функции ![]() следующим образом :
следующим образом :
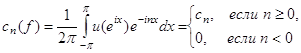
и равенство (10) сразу следует из (2) и (3).
Прежде чем перейти к изучению поведения функции ¦r (x ) при r®1 , отметим некоторые свойства ядра Пуассона:
а) ![]() ;
;
б) 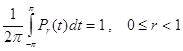 ; (11)
; (11)
в) для любого d>0
![]()
Соотношения а) и в) сразу следуют из формулы (5), а для доказательства б) достаточно положить в (2) и (3) ¦ (х) º 1.![]()
Теорема 1.
Для произвольной (комплекснозначной) функции ![]() ( -p, p ) , 1 £ p < ¥ , имеет место равенство
( -p, p ) , 1 £ p < ¥ , имеет место равенство![]()
![]() ;
;
если же ¦ (x) непрерывна на [ -p, p ] и ¦ (-p) = ¦ (p) , то
![]() .
.
Доказательство.
В силу (3) и свойства б) ядра Пуассона
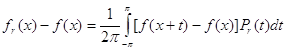 . ( 12 )
. ( 12 )
Для любой функции ![]() , пользуясь неравенством Гельдера и положительностью ядра Пуассона , находим
, пользуясь неравенством Гельдера и положительностью ядра Пуассона , находим![]()
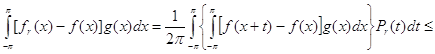
![]()
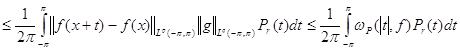 .
.
Следовательно,
![]()
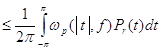 .
.
Для данного e > 0 найдем d = d (e) такое, что ![]() . Тогда для r , достаточно близких к единице, из свойств а)-в) мы получим оценку
. Тогда для r , достаточно близких к единице, из свойств а)-в) мы получим оценку
![]()
![]()
![]() .
.
Аналогично, второе утверждение теоремы 1 вытекает из неравенства
![]()
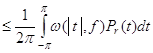 .
.
Теорема 1 доказана.
Дадим определения понятий "максимальная функция" и "оператор слабого типа", которые понадобятся нам в ходе доказательства следующей теоремы.
ОпределениеI.1.
Пусть функция ![]() , суммируема на любом интервале (a,b), a<b,
, суммируема на любом интервале (a,b), a<b, ![]() . Максимальной функцией
для функции
. Максимальной функцией
для функции ![]() называется функция
называется функция
![]() ,
,
где супремум берется по всем интервалам I , содержащим точку х.
Определение I.2.
Оператор ![]() называется оператором слабого типа (р,р)
, если для любого y > 0
называется оператором слабого типа (р,р)
, если для любого y > 0
![]() ,
, ![]() .
.
Теорема 2 (Фату).
Пусть ![]() - комплекснозначная функция из
- комплекснозначная функция из ![]() . Тогда
. Тогда
![]() для п.в.
для п.в. ![]() .
.
Доказательство.
Покажем, что для ![]() и
и ![]()
![]() , ( 13 )
, ( 13 )
где С - абсолютная константа , а M ( f, x ) - максимальная функция для f (x) *) . Для этой цели используем легко выводимую из (5) оценку
![]()
(К - абсолютная константа).
Пусть ![]() - такое число, что
- такое число, что
![]() .
.
Тогда для ![]()
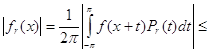
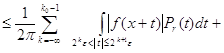
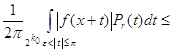
![]()
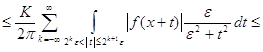
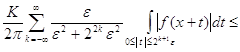
![]() .
.
Неравенство (13) доказано. Возьмем слабый тип (1,1) оператора ![]() . Используя его, найдем такую последовательность функций
. Используя его, найдем такую последовательность функций ![]() ,что
,что
![]() ,
,
![]() ( 14 )
( 14 )
![]() для п.в.
для п.в. ![]() .
.
Согласно (13) при xÎ (-p,p)
![]()
![]()
Учитывая , что по теореме 1 ![]() для каждого xÎ [-p, p] и (14)
для каждого xÎ [-p, p] и (14)
из последней оценки получим
![]() при r®1.
при r®1.
Теорема 2 доказана.
Замечание1.
Используя вместо (13) более сильное неравенство (59), которое мы докажем позже, можно показать, что для п.в. xÎ [-p, p] ![]() , когда точка reit
стремится к eix
по некасательному к окружности
, когда точка reit
стремится к eix
по некасательному к окружности ![]() пути.
пути.
§I.2.Пространства Hp
.
![]()
Определение I.3.
Пространство ![]() - совокупность аналитических в единичном круге функций F (z) , для которых конечна норма
- совокупность аналитических в единичном круге функций F (z) , для которых конечна норма
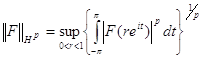 . (15)
. (15)
Пусть комплекснозначная функция ![]() удовлетворяет условиям
удовлетворяет условиям
![]()
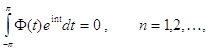 (16)
(16)
тогда функция F (z) , определенная равенством
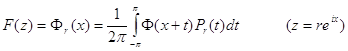 (17)
(17)
принадлежит пространству ![]() , причем
, причем
![]() . (18)
. (18)
![]()
![]() Действительно, аналитичность функции F (z) следует из (16) и равенства (2). Кроме того, в силу неравенства
Действительно, аналитичность функции F (z) следует из (16) и равенства (2). Кроме того, в силу неравенства ![]() мы имеем
мы имеем
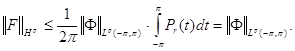 (*)
(*)
С другой стороны , по теореме 1 ( а при р=¥ в силу теоремы 2)
![]() . Отсюда
. Отсюда ![]() (**)
(**)
Учитывая (*) и (**) , получим (18).
Ниже мы докажем, что любую функцию ![]()
![]() можно представить в виде (17). Для этого нам потребуется
можно представить в виде (17). Для этого нам потребуется
Теорема 3.
Пусть комплекснозначная функция j (t) имеет ограниченную вариацию на [ -p,p] и
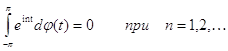 (19)
(19)
Тогда j (t) абсолютно непрерывна на [-p,p].
Замечание2.
В (19) и ниже рассматривается интеграл Лебега-Стилтьеса, построенный по комплекснозначной функции ограниченной вариации j (t) . Мы говорим, что
j (t)= u (t)+ i v (t) имеет ограниченную вариацию (абсолютно непрерывна), если обе действительные функции u (t) и v (t) имеют ограниченную вариацию (соответственно абсолютно непрерывны). При этом интеграл
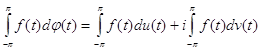
определен для каждой непрерывной на [-p,p] функции f (t) , а также если
![]() - характеристическая функция замкнутого множества
- характеристическая функция замкнутого множества ![]() .
.
Доказательство теоремы 3.
Нам достаточно проверить, что для любого замкнутого множества ![]() ,
,
![]() ,
,
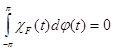 (20)
(20)
Для этой цели убедимся, что справедлива
Лемма 1.
Пусть F
- замкнутое, а V
- открытое множества , причем ![]() и
и
![]() . Тогда для всякого
. Тогда для всякого ![]() , существует функция
, существует функция ![]() вида
вида
![]() , (21)
, (21)
обладающая свойствами:
а) ![]() ;
;
б) ![]() ; (22)
; (22)
в) ![]() .
.
Выведем из леммы 1 оценку (20), а затем докажем саму лемму 1.
Пусть ![]() , где
, где ![]() - конечная или бесконечная последовательность дополнительных интервалов множества F, и для
- конечная или бесконечная последовательность дополнительных интервалов множества F, и для ![]()
![]() .
.
Очевидно, что ![]() - открытое множество и
- открытое множество и ![]() .
.
Рассмотрим для данных ![]() функцию
функцию ![]() , построенную в лемме 1 для числа e и множества
, построенную в лемме 1 для числа e и множества ![]() . Тогда нетрудно проверить[3], что если
. Тогда нетрудно проверить[3], что если ![]() , а
, а ![]() , то разность
, то разность
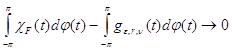 . (23)
. (23)
Но в силу (19) и равномерной сходимости ряда (21) (так как ряд Фурье бесконечно дифференцируемой функции сходится равномерно)
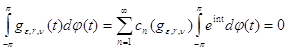 ,
,
и мы получаем равенство (20).
Перейдем к доказательству леммы 1. Нам понадобится
ОпределениеI.4.
Средние Фейера - это средние вида
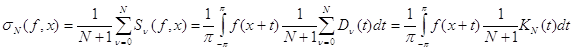
![]() , где
, где ![]() ,
, ![]() ,
, ![]() - ядро Дирихле,
- ядро Дирихле,
![]() ,
, ![]() - ядро Фейера.
- ядро Фейера.
Отметим, что при ![]() ядро Фейера обладает следующими свойствами: а)
ядро Фейера обладает следующими свойствами: а) ![]() ,
, ![]() ; б)
; б) 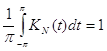 ,
,
Мз которых вытекает, что для ![]() и
и ![]()
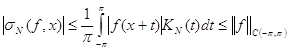 ,
, ![]()
Также известно [3], что средние Фейера ![]() равномерно сходятся к
равномерно сходятся к ![]() .
.
Пусть f(t) - непрерывная на [-p, p] функция, для которой
![]()
![]() и
и ![]()
Так как средние Фейера ![]() равномерно сходятся к
равномерно сходятся к ![]() и
и
![]() , то существует тригонометрический полином
, то существует тригонометрический полином
![]() (24)
(24)
такой, что
![]() (25)
(25)
Пусть ![]() . Рассмотрим для каждого d>0 такую функцию
. Рассмотрим для каждого d>0 такую функцию ![]() , что
, что
![]() ,
, ![]()
![]()
(функцию ![]() можно построить следующим образом: взять замкнутое множество
можно построить следующим образом: взять замкнутое множество ![]() с мерой
с мерой ![]() , достаточно близкой к 2p, и положить
, достаточно близкой к 2p, и положить
![]() ).
).
Так как ![]() (здесь число m то же, что в (24)), то для достаточно малых d>0 функция
(здесь число m то же, что в (24)), то для достаточно малых d>0 функция ![]() удовлетворяет соотношениям
удовлетворяет соотношениям
![]() (26)
(26)
При этом ![]() , если
, если ![]() . Тогда средние Фейера
. Тогда средние Фейера ![]() функции h(t) имеют вид
функции h(t) имеют вид
![]()
и при достаточно большом N
![]() (27)
(27)
Положим
![]() ,
, ![]() (28)
(28)
Так как h(t) - действительная функция, то ![]() , n=0,±1,±2,¼. Поэтому
, n=0,±1,±2,¼. Поэтому
![]() и
и ![]() . (29)
. (29)
Определим искомую функцию g(t) :
![]()
Ясно, что ![]() , а из (24) и (28) следует, что
, а из (24) и (28) следует, что ![]() при n<0, т.е.
при n<0, т.е.
![]() (30)
(30)
В силу соотношений (25), (27) и (29) для ![]()
![]() ,
,
а для ![]()
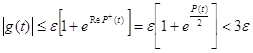 .
.
Наконец, для любого ![]()
![]() .
.
Таким образом, функция g(t) обладает всеми нужными свойствами (22). Лемма1 , а вместе с ней и теорема 3 доказаны.
Теорема 4.
Пусть функция ![]() . Тогда для п.в.
. Тогда для п.в. ![]() существует предел
существует предел
![]() (31)
(31)
При этом
1) 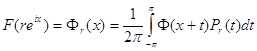 ,
, ![]() ,
, ![]() ;
;
2) ![]()
![]() ;
;
3) ![]()
![]() .
.
Доказательство:
Нам достаточно доказать, что для каждой функции ![]() найдется функция
найдется функция ![]() такая, что имеет место 1). Действительно, если
такая, что имеет место 1). Действительно, если ![]() , то тем более
, то тем более ![]() и из 1) и теоремы 2 вытекает справедливость равенства (31) для п.в.
и из 1) и теоремы 2 вытекает справедливость равенства (31) для п.в. ![]() . При этом
. При этом ![]() и по теореме 1
и по теореме 1 ![]()
![]() . Наконец, из 1) следует, что
. Наконец, из 1) следует, что
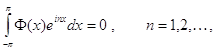
а тогда
![]() .
.
Пусть ![]() . Для построения искомой функции
. Для построения искомой функции ![]() положим
положим
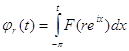 ,
, ![]() ,
, ![]() .
.
Функции ![]() ,
, ![]() , имеют равномерно ограниченную по r вариацию на
, имеют равномерно ограниченную по r вариацию на ![]() :
:
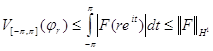 .
.
Следовательно, по теореме Хелли [2] найдутся функция ограниченной вариации ![]() и последовательность
и последовательность ![]() , такие, что
, такие, что ![]() в каждой точке
в каждой точке ![]() и
и
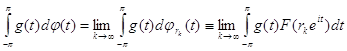 (32)
(32)
для любой функции ![]() . При этом для n=1,2,...
. При этом для n=1,2,...
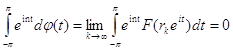
(мы учли аналитичность функции F(z) в единичном круге) и , следовательно, по теореме 3 ![]() абсолютно непрерывна : существует функция
абсолютно непрерывна : существует функция ![]() , для которой
, для которой
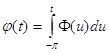 ,
, ![]()
Тогда
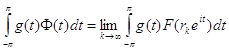 ,
, ![]() (33)
(33)
Зафиксируем число ![]() . Функция
. Функция ![]() , аналитична в круге
, аналитична в круге 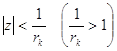 , поэтому согласно утверждению 1
, поэтому согласно утверждению 1
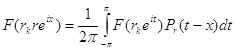 ,
, ![]() .
.
В пределе при ![]() из последнего равенства вытекает, что
из последнего равенства вытекает, что
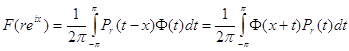 ,
, ![]() ,
, ![]() .
.
Равенство 1) , а вместе с ним и теорема 4 доказаны.
§I.3.Пространства
![]() и
и ![]() .
.
Обозначим через ![]()
![]() класс тех функций
класс тех функций ![]() ,
, ![]() , которые являются граничными значениями функций из
, которые являются граничными значениями функций из ![]() , т.е. представимы в виде
, т.е. представимы в виде
![]() для п.в.
для п.в. ![]() ,
, ![]() .
.
В силу пунктов 3) и 2) теоремы 4 ![]() и каждая функция
и каждая функция ![]() удовлетворяет условию (16). С другой стороны, выше мы доказали, что для произвольной
удовлетворяет условию (16). С другой стороны, выше мы доказали, что для произвольной ![]() с условием (16) интеграл Пуассона (17) определяет функцию из
с условием (16) интеграл Пуассона (17) определяет функцию из ![]() . Следовательно,
. Следовательно,
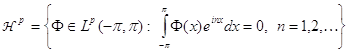 . (34)
. (34)
Из (34) вытекает, что ![]() (замкнутое) - подпространство пространства
(замкнутое) - подпространство пространства ![]() , а
, а ![]() - банахово пространство с нормой (15).
- банахово пространство с нормой (15).
Пусть ![]() . Положим
. Положим
![]() ,
,
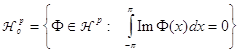 , (35)
, (35)
![]()
ОпределениеI.5.
Если функция ![]() , то сопряженной к ней функцией называется функция
, то сопряженной к ней функцией называется функция 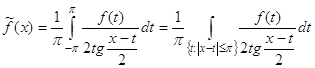 ,
, ![]() ,
,
где интеграл понимается в смысле главного значения, т.е. как предел при ![]() интегралов
интегралов 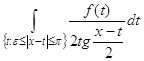 .
.
В дальнейшем нам понадобится
Утверждение2.
Для любой функции ![]() сопряженная функция
сопряженная функция ![]() существует и конечна п.в. на
существует и конечна п.в. на ![]() ; при этом
; при этом
а) ![]() , y>0;
, y>0;
б) если ![]() ,
, ![]() , то
, то ![]() и
и ![]() .
.
Теорема 5.
Следующие условия эквивалентны ![]() :
:
а) ![]() ;
;
б) ![]() ,
, 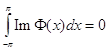 ,
, 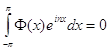 ,
, ![]() ;
;
в) 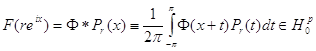 ;
;
г) ![]() , где
, где ![]() - такая действительная функция, что ее сопряженная
- такая действительная функция, что ее сопряженная ![]() также принадлежит пространству
также принадлежит пространству ![]() :
:
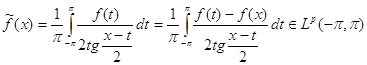 . (36)
. (36)
Доказательство:
Эквивалентность условий а) и б) непосредственно вытекает из (34), а эквивалентность условий а) и в) - из теорем 4 и 2.
Докажем, что из г) следует б). Для этого достаточно проверить, что в случае, когда функция и ее сопряженная суммируемы :![]() , имеют место равенства
, имеют место равенства
![]() ,
, ![]() (37)
(37)
Непосредственный подсчет по формуле (36) показывает, что
![]() ,
, ![]() ,
, ![]() ,
, ![]()
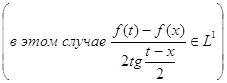 . Следовательно, равенства (37) выполняются, если
. Следовательно, равенства (37) выполняются, если ![]() - произвольный тригонометрический полином.
- произвольный тригонометрический полином.
Пусть ![]() фиксировано. Для произвольной функции
фиксировано. Для произвольной функции ![]() и
и ![]() положим
положим
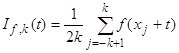 ,
, 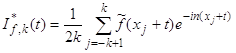 ,
,
где ![]() ,
, ![]() ,
, ![]() .
.
Покажем, что равенство (37) для фиксированного нами номера n вытекает из следующих свойств функций ![]() (наличие этих свойств мы установим ниже):
(наличие этих свойств мы установим ниже):
1) ![]() ,
, ![]() ,
, ![]() ;
;
2) при ![]() функции
функции ![]() ,
, ![]() , сходятся по мере к
, сходятся по мере к
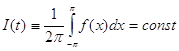 ;
;
3) ![]() ,
, ![]() ,
, ![]() ,
,
где С - абсолютная константа.
Итак, предположим, что имеют место соотношения 1) - 3).
Легко видеть, что ![]() , где
, где ![]() , поэтому из 2) вытекает сходимость по мере последовательности функций
, поэтому из 2) вытекает сходимость по мере последовательности функций ![]() ,
,![]() :
:
![]() по мере
по мере ![]() . (38)
. (38)
Для произвольного ![]() найдем тригонометрический полином
найдем тригонометрический полином ![]() такой, что
такой, что
![]() ,
, ![]() . (39)
. (39)
Тогда согласно 3)
![]() (40)
(40)
и при ![]()
![]() . (41)
. (41)
Так как ![]() - полином, то
- полином, то ![]() и
и
![]() . (42)
. (42)
Учитывая, что ![]() , и пользуясь оценками (40)-(42), мы находим
, и пользуясь оценками (40)-(42), мы находим ![]() ,
, ![]() ,
,
что вместе с (38) доказывает равенство (37).
Докажем теперь, что для произвольной функции ![]() справедливы соотношения 1)-3). Оценка 1) сразу следует из неравенства Чебышева, так как
справедливы соотношения 1)-3). Оценка 1) сразу следует из неравенства Чебышева, так как ![]() .
.
Чтобы доказать 2), фиксируем произвольное ![]() и представим функцию
и представим функцию ![]() в виде
в виде
![]() ,
, ![]() ,
, ![]() . (43)
. (43)
Из непрерывности функции ![]() легко следует, что
легко следует, что
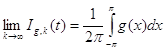
равномерно по ![]() . Поэтому при достаточно больших
. Поэтому при достаточно больших ![]() с учетом (43) мы будем иметь
с учетом (43) мы будем иметь
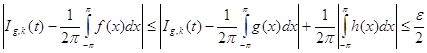 ,
, ![]() (44)
(44)
Кроме того, в силу 1) и (43)
![]() ;
;
из этого неравенства и (44) вытекает, что при ![]()
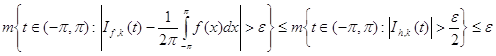 .
.
Для доказательства оценки 3) заметим, что
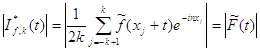 ,
,
где ![]() . Применяя неравенство а) утверждения 2 для функции
. Применяя неравенство а) утверждения 2 для функции ![]() и учитывая, что
и учитывая, что ![]() , получим 3).
, получим 3).
Свойства 1)-3) доказаны. Тем самым установлено, что из условия г) в теореме 5 следует б). Для завершения доказательства теоремы 5 достаточно показать, что из в) вытекает г).
Пусть ![]() (
(![]() ,
,![]() ,
,![]() ) и
) и
![]() . Тогда по теореме 4
. Тогда по теореме 4 ![]() ,
, ![]() и надо доказать только, что
и надо доказать только, что ![]() для п.в.
для п.в. ![]() .
.
Так как ядро Пуассона - действительная функция, мы можем утверждать, что при ![]() и
и ![]()
![]() ,
, ![]() .
.
С другой стороны, из 2), 8) и (37) вытекает, что для любого ![]() ,
,
![]() ,
, ![]() . (45)
. (45)
Согласно теореме 1
![]() . (46)
. (46)
Кроме того, в силу утверждения 2, из сходимости ![]() (
(![]() ) следует сходимость по мере функций
) следует сходимость по мере функций ![]() к
к ![]() . Таким образом,
. Таким образом,
![]() по мере (
по мере (![]() ),
),
а потому , учитывая (46), ![]() для п.в.
для п.в. ![]() .
.
Теорема 5 доказана.
Следствие 1.
а) Если ![]() , то
, то ![]() ;
;
б) если ![]() и
и 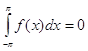 , то
, то ![]() ;
;
в) если ![]() ,
, ![]() ,
, ![]() ,
, ![]() , то
, то
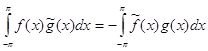 . (47)
. (47)
Доказательство.
Соотношения а) и б) сразу следуют из эквивалентности условий а) и г) в теореме 5.
Чтобы получить в), положим
![]() ,
,
![]() .
.
Согласно теореме 5 ![]() ,
, ![]() , а следовательно,
, а следовательно, ![]() . Но тогда (для п.в.
. Но тогда (для п.в. ![]() )
) ![]() , и из определения класса
, и из определения класса ![]() мы получим, что
мы получим, что
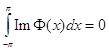 . (48)
. (48)
Из (48) непосредственно вытекает равенство (47).
Замечание 3.
Если ![]() , то в силу п. г) теоремы 5 и утверждения 2 пространство
, то в силу п. г) теоремы 5 и утверждения 2 пространство ![]() совпадает с
совпадает с ![]() . Для р=1 это не так. Пространство
. Для р=1 это не так. Пространство ![]() уже, чем
уже, чем ![]() , и состоит согласно п. г) теоремы 5 из функций
, и состоит согласно п. г) теоремы 5 из функций ![]() , для которых и
, для которых и ![]() .
.
![]() - банахово пространство с нормой
- банахово пространство с нормой
![]() . (49)
. (49)
Полнота ![]() с нормой (49) следует из утверждения 2 и полноты пространства
с нормой (49) следует из утверждения 2 и полноты пространства ![]() : если
: если ![]() при
при ![]() , то
, то ![]() ,
, ![]() ,
, ![]() , и так как
, и так как ![]() по мере при
по мере при ![]() , то
, то ![]() и
и ![]() при
при ![]() .
.
Замечание 4.
Согласно замечанию 3 равенство (47) выполняется, в частности, в случае, когда ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Отметим также, что, взяв в (47) вместо ![]() функцию
функцию ![]() и учитывая б), мы получим
и учитывая б), мы получим
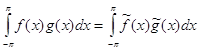 , если
, если 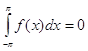 . (50)
. (50)
§I.4.Произведение Бляшке,
нетангенциальная максимальная функция.
Пусть последовательность ненулевых комплексных чисел (не обязательно различных) - ![]() удовлетворяет условию
удовлетворяет условию
![]() ,
, ![]() ,
, ![]() . (51)
. (51)
Рассмотрим произведение(произведение Бляшке)
![]() . (52)
. (52)
Для фиксированного ![]() ,
, ![]() , при
, при ![]() имеет место оценка
имеет место оценка
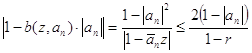 . (53)
. (53)
Так как ряд (51) сходится, то из (53) легко вывести, что произведение (52) сходится абсолютно и равномерно в круге ![]() , т.е. функция
, т.е. функция ![]() аналитична в единичном круге и имеет нули в точках
аналитична в единичном круге и имеет нули в точках ![]() ,
, ![]() , и только в этих точках. При этом, пользуясь неравенством
, и только в этих точках. При этом, пользуясь неравенством ![]() (
(![]() ,
, ![]() ), мы находим
), мы находим
![]() ,
, ![]() . (54)
. (54)
Допустим теперь, что ![]() (
(![]() ) - нули некоторой функции
) - нули некоторой функции ![]() с
с ![]() , причем каждый из них повторяется со своей кратностью. Докажем, что ряд (51) сходится. Положим
, причем каждый из них повторяется со своей кратностью. Докажем, что ряд (51) сходится. Положим
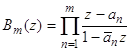 ,
, ![]()
Функция ![]() (
(![]() ) аналитична в круге радиуса больше единицы, и
) аналитична в круге радиуса больше единицы, и ![]() , если
, если ![]() . Следовательно,
. Следовательно, ![]() и согласно п.3 теоремы 4
и согласно п.3 теоремы 4 ![]() . Но тогда
. Но тогда
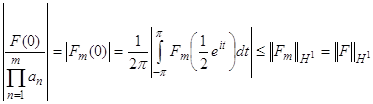
и
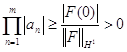 ,
, ![]() (55)
(55)
Так как ![]() ,
, ![]() , то из (55) вытекает сходимость произведения
, то из (55) вытекает сходимость произведения ![]() , а значит, и сходимость ряда (51).
, а значит, и сходимость ряда (51).
ОпределениеI.6.
Пусть ![]() - аналитическая в круге
- аналитическая в круге ![]() функция и
функция и ![]() ,
, ![]() (
(![]() ) - ее нули, повторяющиеся со своей кратностью. Пусть также
) - ее нули, повторяющиеся со своей кратностью. Пусть также ![]() - кратность нуля функции
- кратность нуля функции ![]() при
при ![]() . Произведение
. Произведение
![]() (56)
(56)
называется произведением Бляшке функции ![]() .
.
Справедлива
Теорема 6.
Каждая функция ![]() представима в виде
представима в виде
![]() ,
,
где ![]() не имеет нулей в круге
не имеет нулей в круге ![]() и
и
![]() ,
, ![]() ,
,
а ![]() - произведение Бляшке функции
- произведение Бляшке функции ![]() .
.
Доказательство.
Пусть ![]() ,
, ![]() (
(![]() ) - нули функции
) - нули функции ![]() ( или, что то же самое, нули функции
( или, что то же самое, нули функции ![]() ) Тогда, как отмечалось выше,
) Тогда, как отмечалось выше, ![]() - аналитическая в круге
- аналитическая в круге ![]() функция и
функция и
![]() ,
, ![]() . (57)
. (57)
При этом функция ![]() также аналитична в единичном круге, не имеет в нем нулей и
также аналитична в единичном круге, не имеет в нем нулей и ![]() .
.
Для доказательства обратного неравенства рассмотрим частные произведения (56):
![]() ,
, ![]() ,
, ![]() .
.
Так как ![]() для любого
для любого ![]() , то по теореме 4
, то по теореме 4
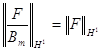
и
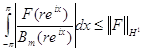 , если
, если ![]() .
.
Устремив в последнем неравенстве число m к бесконечности и учитывая, что ![]() (
(![]() ) равномерно по
) равномерно по ![]() , мы получим
, мы получим
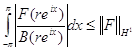 ,
, ![]() ,
,
т.е. ![]() ,
, ![]() .
.
Теорема 6 доказана.
ОпределениеI.7.
Пусть ![]() ,
, ![]() , - произвольное число. Обозначим через
, - произвольное число. Обозначим через ![]() ,
, ![]() , область, ограниченную двумя касательными, проведенными из точки
, область, ограниченную двумя касательными, проведенными из точки ![]() к окружности
к окружности ![]() , и наибольшей из дуг окружности, заключенных между точками касания ( при
, и наибольшей из дуг окружности, заключенных между точками касания ( при ![]()
![]() вырождается в радиус единичного круга). Для
вырождается в радиус единичного круга). Для ![]() положим
положим
![]() ,
, ![]() ,
,
где ![]() - интеграл Пуассона функции
- интеграл Пуассона функции ![]() . Функция
. Функция ![]() называется нетангенциальной максимальной функцией для
называется нетангенциальной максимальной функцией для ![]() .
.
В силу теоремы 2
![]() для п.в.
для п.в. ![]() . (58)
. (58)
Установим, что для произвольной функции ![]() величина
величина ![]() не превосходит (по порядку) значения максимальной функции
не превосходит (по порядку) значения максимальной функции ![]() *)
в точке х, т.е.
*)
в точке х, т.е.
![]() ,
, ![]() . (59)
. (59)
Нам понадобится
утверждение 3.
а) если функция ![]() , то для любого
, то для любого ![]()
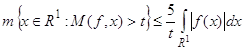 ;
;
б) если функция ![]() ,
,![]() то
то ![]() ,
,
где ![]() - постоянная, зависящая только от числа р.
- постоянная, зависящая только от числа р.
Пусть ![]() и
и ![]() . По определению интеграла Пуассона
. По определению интеграла Пуассона
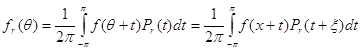
Положим 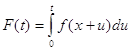 . Тогда будем иметь
. Тогда будем иметь
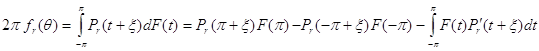
и, в силу неравенства ![]() ,
, ![]() , и периодичности
, и периодичности ![]() ,
,
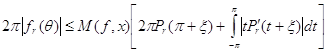 . (60)
. (60)
Так как обе функции ![]() и
и ![]() положительны при
положительны при ![]() и отрицательны при
и отрицательны при ![]() ( из (5)), то, предполагая без ограничения общности, что
( из (5)), то, предполагая без ограничения общности, что ![]() , мы получим
, мы получим
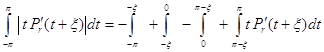 . (61)
. (61)
Для ![]() имеют место оценки
имеют место оценки
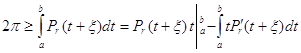 ,
,
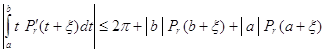 .
.
Следовательно, для доказательства неравенства (59) достаточно проверить, что
![]() при
при ![]() , (62)
, (62)
если ![]() . Пусть
. Пусть ![]() , тогда
, тогда
![]() .
.
В остальных случаях неравенство (62) очевидно. Из (58), (59) и утверждения 3 вытекает, что для любой функции ![]() ,
, ![]() ,
,
![]() , (63)
, (63)
где ![]() - постоянная, зависящая только от
- постоянная, зависящая только от ![]() .
.
Теорема 7.
Пусть ![]() (
(![]() ),
), ![]() и
и
![]() ,
, ![]() .
.
![]() Тогда
Тогда ![]() и
и
![]() . (64)
. (64)
Доказательство.
Утверждение теоремы 7 в случае, когда ![]() , есть прямое следствие оценки (63) и теоремы 4. Пусть теперь
, есть прямое следствие оценки (63) и теоремы 4. Пусть теперь ![]() . По теореме 6
. По теореме 6 ![]() , где
, где ![]() ,
, ![]() , если
, если ![]() и
и ![]() . Из функции
. Из функции ![]() можно извлечь корень: существует функция
можно извлечь корень: существует функция ![]() такая, что
такая, что ![]() , и, следовательно из (64) при р=2, получим
, и, следовательно из (64) при р=2, получим
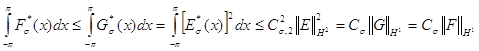 .
.
Оценка снизу для ![]() вытекает из (58).
вытекает из (58).
Теорема 7 доказана.
Глава II. Атомические разложения функции
в пространстве
![]() , пространство ВМО.
, пространство ВМО.
§II.1.Пространство
![]() , критерий принадлежности функции из
, критерий принадлежности функции из ![]()
пространству
![]() .
.
Рассмотрим ![]() (
(![]() ) - пространство функций
) - пространство функций ![]() , являющихся граничными значениями действительных частей функций из пространства
, являющихся граничными значениями действительных частей функций из пространства ![]() :
:
![]() для п.в.
для п.в. ![]() ,
, ![]() . (65)
. (65)
Ранее мы доказали, что
![]() ,
, ![]() , (66)
, (66)
и что ![]() - банахово пространство с нормой
- банахово пространство с нормой
![]() ; (67)
; (67)
при этом, если в (65) ![]() , то
, то
![]() (
(![]() ) . (68)
) . (68)
В замечании 3 уже говорилось о том, что при ![]() пространство
пространство ![]() совпадает с пространством
совпадает с пространством ![]() и из утверждения 2 следует, что
и из утверждения 2 следует, что
![]() (
(![]() ).
).
Последнее соотношение теряет силу при ![]() - нетрудно проверить, что при
- нетрудно проверить, что при ![]()
![]() ,
,
где
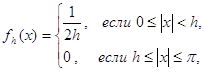
и, следовательно, существует функция ![]() , для которой
, для которой ![]() . Таким образом,
. Таким образом, ![]() - собственное подпространство в
- собственное подпространство в ![]() . Ниже мы дадим критерий принадлежности функций к пространству
. Ниже мы дадим критерий принадлежности функций к пространству ![]() .
.
ОпределениеII. 8.
Множество ![]() мы будем называть обобщенным интервалом, если
мы будем называть обобщенным интервалом, если ![]() - дуга на единичной окружности, т.е.
- дуга на единичной окружности, т.е. ![]() - либо интервал из
- либо интервал из ![]() , либо множество вида
, либо множество вида
![]() (
(![]() ). (69)
). (69)
Точку ![]() назовем центром обобщенного интервала
назовем центром обобщенного интервала ![]() , если
, если ![]() - центр дуги
- центр дуги ![]() . Длиной обобщенного интервала
. Длиной обобщенного интервала ![]() естественно назвать величину
естественно назвать величину
![]()
Определение II.9.
Действительную функцию ![]() назовем атомом, если существует обобщенный интервал
назовем атомом, если существует обобщенный интервал ![]() такой, что
такой, что
а) ![]() ;
;
б) 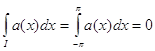 ;
;
в) ![]() .
.
Атомом назовем также функцию ![]() ,
, ![]() .
.
Теорема 8.
Для того, чтобы выполнялось включение: ![]() , необходимо и достаточно, чтобы функция
, необходимо и достаточно, чтобы функция ![]() допускала представление в виде
*)
допускала представление в виде
*)
![]() ,
, ![]() , (70)
, (70)
где ![]() ,
, ![]() , - атомы. При этом
, - атомы. При этом
![]() , (71)
, (71)
где inf берется по всем разложениям вида (70) функции ![]() , а с и С
, а с и С ![]() - абсолютные константы.
- абсолютные константы.
Доказательство.
Достаточность.
Пусть для функции ![]() нашлось разложение вида (70). Покажем, что
нашлось разложение вида (70). Покажем, что ![]() и
и ![]() . Для этого достаточно проверить, что для любого атома
. Для этого достаточно проверить, что для любого атома ![]() имеет место неравенство
имеет место неравенство
![]() . (72)
. (72)
Пусть ![]() - такой обобщенный интервал, что
- такой обобщенный интервал, что
![]() ,
, ![]() ,
, ![]() (73)
(73)
(случай ![]() тривиален). Так как
тривиален). Так как 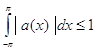 , то нам остается доказать, что
, то нам остается доказать, что
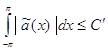 . (74)
. (74)
Для любого измеримого множества ![]() , применяя неравенство Коши и пользуясь утверждением 2 и соотношениями (73), мы находим
, применяя неравенство Коши и пользуясь утверждением 2 и соотношениями (73), мы находим
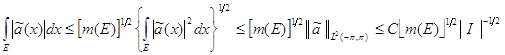 , (75)
, (75)
откуда сразу вытекает (74), в случае, когда ![]() .
.
Допустим теперь, что ![]() , и обозначим через
, и обозначим через ![]() обобщенный интервал длины
обобщенный интервал длины ![]() с тем же центром, что и
с тем же центром, что и ![]() . Из (75) следует, что
. Из (75) следует, что
![]() .
.
Нам остается оценить интеграл ![]() . Мы воспользуемся очевидным неравенством
. Мы воспользуемся очевидным неравенством
![]() ,
, ![]() ,
,
где ![]() - длина наименьшей из двух дуг единичной окружности, соединяющих точки
- длина наименьшей из двух дуг единичной окружности, соединяющих точки ![]() и
и ![]() , а
, а ![]() - абсолютная постоянная. В силу (73) при
- абсолютная постоянная. В силу (73) при ![]() мы имеем
мы имеем
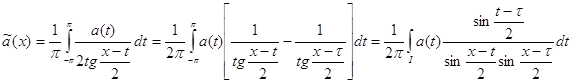 где
где ![]() - центр обобщенного интервала
- центр обобщенного интервала ![]() . Из последнего соотношения, учитывая, что
. Из последнего соотношения, учитывая, что ![]() и
и ![]() , мы находим
, мы находим
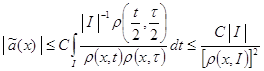 ,
, ![]() , где
, где ![]() .
.
Следовательно,
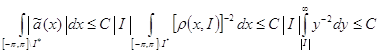 .
.
Оценка (74), а потому и оценка (72) доказаны.
Необходимость.
Построим для данной функции ![]() разложение (70), для которого
разложение (70), для которого
![]() .
.
Пусть функция ![]() с
с ![]() такова, что выполнено соотношение (65), и пусть
такова, что выполнено соотношение (65), и пусть ![]() (
(![]() ) - нетангенциальная максимальная функция для
) - нетангенциальная максимальная функция для ![]() , т.е.
, т.е.
![]() ,
, ![]() , (75')
, (75')
где ![]() - область, ограниченная двумя касательными, проведенными из точки
- область, ограниченная двумя касательными, проведенными из точки ![]() к окружности
к окружности ![]() , и наибольшей дугой окружности
, и наибольшей дугой окружности ![]() , заключенной между точками касания.
, заключенной между точками касания.
Теорема 7 утверждает, что ![]() , поэтому нам достаточно найти такое разложение функции
, поэтому нам достаточно найти такое разложение функции ![]() на атомы (70), что
на атомы (70), что
![]() , (76)
, (76)
где постоянные С и ![]() (
(![]() ) не зависят от
) не зависят от ![]() . Для построения разложения (70) с условием (76) фиксируем число
. Для построения разложения (70) с условием (76) фиксируем число ![]() : пусть, например,
: пусть, например, ![]() . Не ограничивая общности, мы можем считать, что
. Не ограничивая общности, мы можем считать, что
![]() . (77)
. (77)
Рассмотрим на отрезке ![]() множества
множества
![]() ,
, ![]() ,
, ![]() (78)
(78)
Так как при любом ![]() множество точек единичной окружности
множество точек единичной окружности ![]() открыто, то ясно, что при
открыто, то ясно, что при ![]() множество
множество ![]() (если оно непустое) представимо (единственным образом) в виде суммы непересекающихся обобщенных интервалов:
(если оно непустое) представимо (единственным образом) в виде суммы непересекающихся обобщенных интервалов:
![]() ,
, ![]() при
при ![]() ,
, ![]() ,
, ![]() . (79)
. (79)
Положим 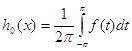 и при
и при ![]()
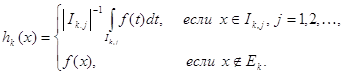 (80)
(80)
Так как ![]() конечна для п.в.
конечна для п.в. ![]() , то из определения функций
, то из определения функций ![]() ,
, ![]() , следует, что для п.в.
, следует, что для п.в. ![]()
![]() при
при ![]() , а значит, для п.в.
, а значит, для п.в. ![]()
![]() .
.
Отсюда, учитывая, что ![]() , а следовательно из (80),
, а следовательно из (80), ![]() при
при ![]() , мы находим, что
, мы находим, что
![]() , (81)
, (81)
где ![]() - характеристическая функция множества
- характеристическая функция множества ![]() . Из (81), учитывая, что
. Из (81), учитывая, что ![]() , мы для функции
, мы для функции ![]() получаем следующее разложение:
получаем следующее разложение:
![]() для п.в.
для п.в. ![]() , (82)
, (82)
где
![]() ,
, ![]() ,
, ![]() (83)
(83)
С помощью функций ![]() мы и построим нужное нам разложение вида (70). Прежде всего отметим, что при
мы и построим нужное нам разложение вида (70). Прежде всего отметим, что при ![]() ,
, ![]()
![]() ,
, ![]() . (84)
. (84)
Докажем теперь, что для п.в. ![]()
![]() ,
, ![]() , (85)
, (85)
где постоянная ![]() зависит только от числа
зависит только от числа ![]() , зафиксированного нами ранее.
, зафиксированного нами ранее.
Так как из (65) и (75') ![]() для п.в.
для п.в.![]() , то из (77) следует, что
, то из (77) следует, что
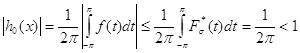 .
.
Пусть теперь ![]() ,
, ![]() - один из обобщенных интервалов в представлении (79), тогда из (77) и (78)
- один из обобщенных интервалов в представлении (79), тогда из (77) и (78) ![]() , и если
, и если ![]() ,
, ![]() - концевые точки дуги
- концевые точки дуги ![]() (
(![]() ) , то
) , то ![]() , а значит,
, а значит,
![]() ,
, ![]() . (86)
. (86)
Из неравенств (86) согласно (75') следует, что
![]() при
при ![]() . (87)
. (87)
Легко видеть (учитывая, что ![]() и
и ![]() ) , что множества
) , что множества ![]() и
и ![]() пересекаются в одной точке:
пересекаются в одной точке:
![]() с
с ![]() ,
, ![]() . (88)
. (88)
Пусть ![]() ,
, ![]() , - отрезок, соединяющий точки
, - отрезок, соединяющий точки ![]() и
и ![]() . Так как
. Так как ![]() ,
, ![]() , то из непрерывности функции
, то из непрерывности функции ![]() при
при ![]() и неравенства (87) вытекает, что
и неравенства (87) вытекает, что ![]() , если
, если ![]() ,
, ![]() , и
, и ![]() . Поэтому , учитывая (88)
. Поэтому , учитывая (88)
![]() ,
, ![]() ,
,![]() ,
, ![]() . (89)
. (89)
Рассмотрим область отрезками пусть, далее, для
|
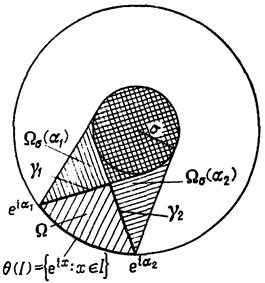 |
По теореме Коши [5] ![]() .
.
Отсюда и из (89), учитывая, что для любой дуги ![]() справедливо равенство
справедливо равенство 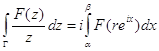 ,
,
мы получим
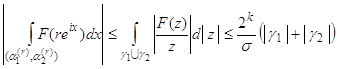 .
.
Но в силу теорем 4 и 5
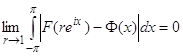 ,
, ![]() ,
,
и так как ![]() ,
, ![]() , то мы находим, что
, то мы находим, что
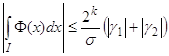 . (89')
. (89')
Легко видеть, что отношение ![]() ограничено сверху числом, зависящим только от s, поэтому
ограничено сверху числом, зависящим только от s, поэтому
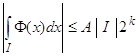 ,
, ![]() . (90)
. (90)
Так как ![]() , то из соотношений (90) и (80) вытекает, что для
, то из соотношений (90) и (80) вытекает, что для ![]() ,
, ![]() , справедливо неравенство (85). Для п.в.
, справедливо неравенство (85). Для п.в. ![]() неравенство (85) сразу следует из определения функций
неравенство (85) сразу следует из определения функций ![]() и множеств
и множеств ![]() .
.
Пользуясь оценкой (85) , из (83) мы получаем, что ![]() , а это значит, что функции
, а это значит, что функции
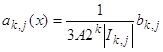 ,
, ![]() ,
, ![]() ,
,
являются атомами. Тогда, преобразуя неравенство (82), мы получаем разложение функции ![]() на атомы:
на атомы:
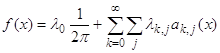 для п.в.
для п.в. ![]() ,
,
где 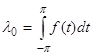 ,
, ![]() .
.
Оценим сумму модулей коэффициентов указанного разложения. Учитывая равенство (77), имеем
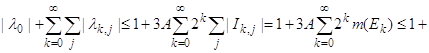
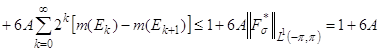 .
.
Неравенство (76), а потому и теорема 8 доказаны.
§II.2. Линейные ограниченные функционалы на
![]() , двойственность
, двойственность ![]() и ВМО.
и ВМО.
Дадим описание пространства ![]() , сопряженного к банахову пространству
, сопряженного к банахову пространству ![]() . Нам потребуется
. Нам потребуется
Определение II.10.
Пространство ВМО есть совокупность всех функций ![]() , удовлетворяющих условию
, удовлетворяющих условию
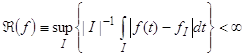 , (91)
, (91)
где ![]() , а sup берется по всем обобщенным интервалам
, а sup берется по всем обобщенным интервалам ![]() .
.
Нетрудно убедится, что ВМО является банаховым пространством с нормой
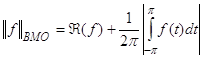 . (92)
. (92)
Ясно, что ![]() . В то же время ВМО содержит и неограниченные функции. Нетрудно проверить, например, что функция
. В то же время ВМО содержит и неограниченные функции. Нетрудно проверить, например, что функция ![]() .
.
Теорема 9.
![]() , т.е.
, т.е.
а) если ![]() , и для произвольной функции
, и для произвольной функции ![]() рассмотреть ее разложение на атомы (по теореме 8):
рассмотреть ее разложение на атомы (по теореме 8):
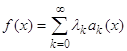 ,
, 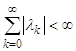 ,
, ![]() ,
, ![]() - атомы
*)
(93)
- атомы
*)
(93)
и положить
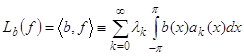 , (94)
, (94)
то сумма ![]() ряда (94) конечна, не зависит от выбора разложения (93) и задает ограниченный линейный функционал на
ряда (94) конечна, не зависит от выбора разложения (93) и задает ограниченный линейный функционал на ![]() ;
;
б) произвольный ограниченный линейный функционал ![]() на
на ![]() представим в виде (94), где
представим в виде (94), где ![]() . При этом
. При этом
![]()
(С, С1 - абсолютные постоянные).
Лемма 2.
Пусть функция ![]() такова, что для любого обобщенного интервала
такова, что для любого обобщенного интервала ![]() найдется постоянная
найдется постоянная ![]() , для которой
, для которой
![]() ,
,
где М не зависит от ![]() . Тогда
. Тогда ![]() и
и ![]() .
.
Доказательство.
Для любого обобщенного интервала ![]() мы имеем
мы имеем
![]() ,
,
откуда согласно (91) получаем утверждение Леммы 2.
Следствие 2.
Если ![]() , то
, то ![]() и
и
![]() . (95)
. (95)
Следствие 2 непосредственно вытекает из леммы 2, если учесть, что
![]()
для произвольного обобщенного интервала ![]() .
.
Доказательство теоремы 9.
а) Пусть ![]() . Положим
. Положим
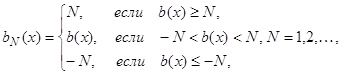
Так как всегда ![]() , то, учитывая равенства
, то, учитывая равенства
![]() ,
, ![]() ,
, ![]()
![]() ,
,
мы с помощью следствия 2 находим
![]() ,
, ![]() (96)
(96)
Допустим, что ![]() ( по утверждению 2 и (66)). По теореме 8 существует разложение
( по утверждению 2 и (66)). По теореме 8 существует разложение
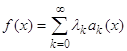 ,
, 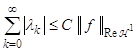 , (97)
, (97)
где функции ![]() являются атомами и
являются атомами и ![]() , и при
, и при ![]()
![]() ,
, 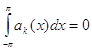 ,
, ![]() . (98)
. (98)
Из соотношений (96), (97) и (98) вытекает, что при ![]()
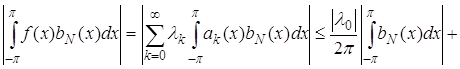
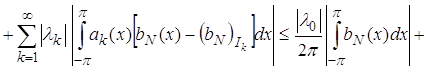
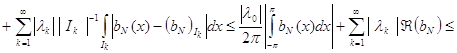
![]()
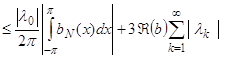 .
.
Отсюда, учитывая, что функции ![]() ,
, ![]() , по модулю не превосходят суммируемой функции
, по модулю не превосходят суммируемой функции ![]() и для п.в.
и для п.в. ![]()
![]() , мы получим, что
, мы получим, что
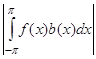
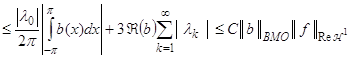 .
.
Таким образом, равенством
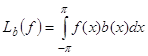 ,
, ![]() , (99)
, (99)
определяется ограниченный линейный функционал на всюду плотном в ![]() линейном многообразии (плотность функций из
линейном многообразии (плотность функций из ![]() в
в ![]() вытекает из теоремы 8, так как для всякой функции
вытекает из теоремы 8, так как для всякой функции ![]() частные суммы разложения (70) сходятся к
частные суммы разложения (70) сходятся к ![]() по норме
по норме ![]() , и, очевидно, принадлежат пространству
, и, очевидно, принадлежат пространству ![]() ). Поэтому функционал
). Поэтому функционал ![]() можно единственным образом продолжить на все пространство
можно единственным образом продолжить на все пространство ![]() :
:
![]() ,
, ![]() . (100)
. (100)
Остается доказать, что для любого разложения вида (93) функции ![]() ряд (94) сходится и его сумма равна
ряд (94) сходится и его сумма равна ![]() . Последнее сразу следует из (99) и сходимости ряда (93), по норме
. Последнее сразу следует из (99) и сходимости ряда (93), по норме ![]() к
к ![]() :
:
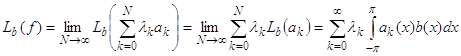 .
.
б) Пусть L - произвольный ограниченный линейный функционал на ![]() . Тогда из теоремы 4.1 и (67) для любой функции
. Тогда из теоремы 4.1 и (67) для любой функции ![]()
![]()
(С - абсолютная постоянная). Это значит, что L - ограниченный линейный функционал на ![]() , а следовательно, найдется функция
, а следовательно, найдется функция ![]() с
с
![]() , (101)
, (101)
для которой
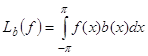 ,
, ![]() . (102)
. (102)
В частности, равенство (102) выполняется, если ![]() - произвольный атом. Докажем, что
- произвольный атом. Докажем, что
![]() . (103)
. (103)
Пусть I - произвольный обобщенный интервал, ![]() - произвольная функция с
- произвольная функция с ![]() . Тогда функция
. Тогда функция
![]() ,
, ![]() ,
,
является атомом и в силу теоремы 8 ![]() . Поэтому
. Поэтому
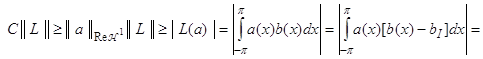
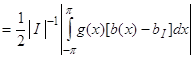 .
.
Подбирая в последнем неравенстве функцию ![]() оптимальным образом, мы получим, что для любого обобщенного интервала I
оптимальным образом, мы получим, что для любого обобщенного интервала I
![]() ,
,
что с учетом соотношения 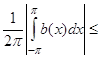
![]() доказывает оценку (103).
доказывает оценку (103).
Таким образом, для ![]() значение функционала
значение функционала ![]() совпадает со значением ограниченного линейного функционала
совпадает со значением ограниченного линейного функционала ![]() на элементе
на элементе ![]() (см. (99) и уже доказанное утверждение а) теоремы 9). Так как пространство
(см. (99) и уже доказанное утверждение а) теоремы 9). Так как пространство ![]() плотно в
плотно в ![]() , то, следовательно,
, то, следовательно,
![]()
![]() для любой функции
для любой функции ![]() .
.
Полученное равенство завершает доказательство теоремы 9.
Литература
1. Кашин Б.С., Саакян А.А. Ортогональные ряды — М.: Наука, 1984.—495с.
2. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа — М.: Наука, 1989. — 623с.
3. Тер-Крикоров А.М., Шабунин М.И. Курс математического анализа — М.: Наука, 1988. —815с.
4. Бари Н.К. Тригонометрические ряды —М.: Гос. издательство физико-математической литературы, 1961. —936с.
5. Маркушевич А.И. Краткий курс теории аналитических функций - М.: Наука, 1978. — 415с.
6. Дж.Гарнетт Ограниченные аналитические функции — М.: Мир, 1984. - 469с.
7. Фихтенгольц Г.М. Основы математического анализа — М.: Наука, 1964.—т.2,—463с.
8. Вартанян Г.М. Аппроксимативные свойства и двойственность некоторых функциональных пространств — Одесса, 1990 —111с.
*) Мы считаем , что f (x) = 0 , если |x | > p .
*) Так как функция определялась для функций , заданных на , то мы дополнительно полагаем , если ; при и при .
*) В силу условий а) и в) в определении 9 , , поэтому ряд (70) сходится по норме пространства и п.в.
*) Возможен случай, когда при .
Похожие работы
-
Стійкість системи лінійних алгебраїчних рівнянь
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ КАФЕДРА ІНФОРМАТИКИ Курсова робота по чисельним методам на тему:”Стійкість СЛАР”
-
Теорія ймовірностей та математична статистика
Міністерство освіти і науки України Донбаський державний технічний університет Кафедра Вищої Математики КОНТРОЛЬНА РОБОТА По дисципліні “Теорія ймовірностей та математична статистика”
-
Вычисление определенных интегралов. Квадратурные формулы
Решение задачи по вычислению определенного интеграла с помощью квадратурных формул и основная идея их построения. Количество параметров квадратурного выражения, степень подынтегральной функции. Построение квадратурных формул с плавающими узлами.
-
Система лінійних однорідних алгебраїчних рівнянь Фундаментальна сукупність розвязків
Міністерство освіти і науки України Закарпатський державний університет ІНСТИТУТ ІНФОРМАТИКИ КАФЕДРА ФІЗИКО-МАТЕМАТИЧНИХ ДИСЦИПЛІН Реєстраційний №____
-
Алгоритми та Чисельні методи
Національний технічний університет України «КПІ» Факультет Інформатики та Обчислювальної техніки Кафедра Обчислювальної Техніки Лабораторна робота №2-1
-
Обчислення матричних задач
МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ Бердичівський політехнічний коледж Контрольна робота з дисципліни “Числові методи” Виконав: студент групи Пзс-503 Лифар Сергій Олександрович
-
Наведення усіх перестановок елементів множини
Перестановка як перевпорядкованість наборів елементів, об’єктів або функція, що задає таку перевпорядкованість. Всі можливі варіанти перестановок елементів множини за умови наявності трьох елементів за умови, що жоден елемент не залишається на місці.
-
Побудова скінченних множин
Множина як визначена сукупність елементів чи об’єктів. Списковий спосіб подання множини. Множина, кількість елементів якої скінченна (скінченна множина). Виведення декартового добутку з кожної заданої комбінації. Алгоритм рішення та реалізація програми.
-
Прикладне вживання методів дискретної математики
МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ Бердичівський політехнічний коледж Контрольна робота Прикладне вживання методів дискретної математики м. Бердичів 2007 р.
-
Метод скінчених різниць в обчислювальній математиці
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ кафедра інформатики КОНТРОЛЬНА Р БОТА ПО КУРСУ: Чисельні методи на тему: «Метод скінчених різниць в обчислювальній математиці»