Название: Матанализ

Вид работы: реферат

Рубрика: Математика

Размер файла: 34.45 Kb

Скачать файл: referat.me-216923.docx

Краткое описание работы: 1Натуральные числа – 1,2,3,4, …., счёт предметов, указание порядкового номера. Натуральные числа также называют положительными целыми числами. Числа –1,-2, -3, …, противоположные натуральным называются отрицательными целыми числами. Число 0 тоже целое. Рациональные числа – целые и дроби (+,-) Вид М/N, где (N

Матанализ

1Натуральные числа – 1,2,3,4, …., счёт предметов, указание порядкового номера. Натуральные числа также называют положительными целыми числами. Числа –1,-2, -3, …, противоположные натуральным называются отрицательными целыми числами. Число 0 тоже целое. Рациональные числа – целые и дроби (+,-) Вид М/N, где (N0)M и N- взаимно простые целые числа. Иррациональные - √2 все вышепереч-е + бесконечные непериодич. дроби. Все эти числа – действительные. Компл. число Z1=A1+iB1; i²=-1

2 Z1±Z2=(A1±A2)+i(B1±B2)

Z1*Z2=(A1+iB1)*(A2+iB2)

Z1/Z2=(a1+ib1)(a2-ib2)/(a2+ib2)(a2-ib2)=(a1a2+b1b2)+

i(b1a2-a1b2)a2²+b2²=(a1a2+b1b2/a2²+b2²)+i* (b1a2-

a1b2/a2²+b2²)

3 Тигонометрическая форма комплексного числа

Z=a+ib=r*cosφ+i*r*sinφ=r*(cosφ+i*sinφ)

r – модуль; φ – аргумент. b – y; a – x.

4 Zª=rª(cos Aφ+i*sin Aφ)

5 ª√Z=ª√r(cos φ+2πk/а +i *sin φ+2πk/a) k∈(1;2;3…a-1)

Все корни А-ой степени лежат на окружности r=| Z |¹а и являются вершинами правильного А-угольника, вписанного в эту окружность.

6 Переменная вел. Х, принимающая последовательно ( с возрастанием номера n ) значения х1,х2,х3..хN называется числовой последовательностью

1,1,1,1,1…1

1,1/2,1/3…1/N

1,-1,1,-1…(-1)ª

Xn,n∈N

Число А наз. пределом последовательности Хn если для любого сколь угодно малого положит. числа E>0 найдётся такой номер N(E), что как только n>N(E) то имеет место неравенство | Xn – A | < E

lim Xn = A

n→∞

Число А есть предел последовательности Xn если для любого ε> 0 найдётся такой номер N, начиная с которого (при n>N) все члены последовательности будут заключены в ε-окрестности какой бы она узкой ни была. Вне этой окрестности может быть лишь конечное число членов этой последовательности.

7 Если последовательность Хn монотонна и ограничена, то она имеет предел (сходится).

Cвойства пределов:

если Хn=С то lim Xn=C

n→∞

пусть lim Xn=A, a lim Yn=B тогда lim (Xn±Yn)=A±B

n→∞ n→∞ lim (Xn*Yn)=A*B

lim (Xn/Yn)=A/B ; B≠0

если Xn≤Yn для n∈N то lim Xn ≤ lim Yn

n→∞ n→∞

8 Eсли Хn сходится (имеет предел) то Хn ограничена

Последовательность Xn; n∈N наз. ограниченнойесли существует положительное число М, что выполняется нер-во | Xn |≤M; n∈N

Если lim Xn=0, то Xn; n∈N наз. БМВ обознач (αn,βn,γn)

n→∞

Св-ва БМВ:

lim αn=0

n→∞

lim (αn±βn)=0

n→∞

lim (Xn*αn)=0; если Xn-ограничена

n→∞

В произведении БМВ можно заменять на эквивалентную БМ. В алгебраической сумме замену можно производить в том случае если не происходит сокращения БМ одного порядка с Х:

sin X ~ X eª-1 ~ a

tg X ~ X (1+x)ª ~ ax

1 – cos X ~ X²/2 arctg X ~ X

LOGe(1+X) ~ X xª-1 ~ aLNx

9 Сумма эл-тов числовой последовательности наз. числовым рядом.

Сумма n членов ряда – n частичная сумма ряда

Если при n→∞ lim Sn=S, то ряд сходящийся, S сумма ряда .

Ряд наз. сходящимся если сущ. конечный предел последовательности его частичных сумм.

Прим:

при каких q сходится и расходится ?

сходится к сумме S=a/1-q при | q |<1 и расход-ся при | q |≥1

10 Признак сравнения двух знакоположит-х рядов.

есть 2 знакполож. ряда ∑Ak,∑Bk так что 0≤Ak≤Bk k∈N

тогда если ∑Bk⇒то ∑Ak тоже ⇒ и наооборот если меньший ряд не сходится то и больший тоже.

11Признак Даламбера

∑Un c положительными членами сущ. lim Un+1/Un =l

n→∞

то ряд сходится если l<1 и расходится если l>1, если l=1 то вопрос о сходимости нерешён.

Признак Коши

∑An – знакополож. ряд lim ª√An=q

n→∞

q<1 – сходится ; q>1 – расходится.

12 Знакопеременный ряд а1-а2+а3-а4…+ (-1)в степ.(n-1)*An

An>0

Признак Лейбница:

Если члены ряда (знакопер) убывают а1>a2>a3>…An и

предел Аn при n→∞ =0 то ряд сходится

пример 1-1/2+1/3-1/4…+(-1)(n-1)*1/n

13 Имеет место функциональная зависимость между двумя переменными величинами х и у если задан закон y=f(x), согласно которому каждому х∈Х соответствует значение y∈Y. х-аргумент

y=kx+b – линейная ф-ия

y=ax²+bx+c – квадратичная ф-ия

Обратная ф-ия – ф-ия x=φ(y) наз. обратной ф-ией к прямой ф-ии y=f(x) если x=φ(f(x)) для всех х∈Х

Графики взаимно обратных ф-ий симметричны относительно прямой у=х.

y=Xª и y=LOGxA – примеры

14 Число B называется пределом ф-ии в f(x) при x, стремящемуся к x0 (или в точке x0) если для любого, сколь угодно малого положительного числа ε>0, найдётся такое положительное число δ(ε)>0 что для всех х не равных х0 и удовлетворяющих условию | x-x0 |<δ выполняется нерав-во | f(x)-B | < ε

lim f(x)=B

x→x0

Смысл состоит в том, что для всех значений х, достаточно близких к х0, значения ф-ии f(x) как угодно мало отличаются от числа В (по модулю)

15 lim f(x)=B

x→x0

Если B=f(x0), то ф-ия f(x) – непрерывна в точке х0.

св-ва :

lim c=c

x→x0

если f(x)=b, φ(x)=c то lim (f(x)±φ(x))=b±c

x→x0

lim (f(x)*φ(x))=b*c

x→x0

lim (f(x)/φ(x))=b/c (c≠0)

x→x0

Если f(x)≤φ(x)≤g(x) и lim f(x)=lim g(x) =b то lim φ(x)=b

x→x0 x→x0 x→x0

если при этом b=f(x0); c=φ(x0) то св-во 2 можно записать:

(Если f(x) или φ(х) непрерывны в т. х0 то в т.х0

непрерывны сумма, разность, произведение и

частное(φ(х0))≠0 этих функций

Если ф-ия непрерывна в каждой точке отрезка, то она непрерывна на этом отрезке

16 Линейная ф-ия непрерывна в любой точке А∈(-∞;+∞)

y=kx+b=f(x)

f(A)=kA+b

k≠0 ⇒ | f(x)-f(a) |<ε | kx-b-ka+b | <ε

| k (x-f) | <ε

| k |*| x-a | <ε

| x-a | < ε/| k |=δ(ε)

y=ax²+bx+c (-∞;+∞)

17 y=Bª (B>0)

Докажем, что y=Bª непрерывна на (-∞;+∞)

lim Bª=1

a→0

| Bª-1 | <ε 1) B=1

2) B>1

-ε < Bª-1 < ε 1-ε < Bª < ε+1

LOGb(1-ε)<a<LOGb(1+ε)

min {-LOGa(1-ε); LOGa(1+ε)}= δε

| x | < δε

LOGaB

18 y=cos x (-∞; +∞)

| cos x – cos a | < ε

| 2 sin (x-a)/2 + sin (x+a)/2 | < ε

2 | sin (x-a)/2 | + | sin (x+a)/2 | < ε

2 | sin (x-a)/2 | < ε

| x-a | < ε =δ(ε)

y=sin x (-∞; +∞)

y=tg x=sin x/cos x кроме x=π/2+πk

y=ctg x=cos x/sin x кроме x=πk

19 Первым замечательным пределом называется

lim sin x/x=1

x→x0

20 Второй замечательный предел

lim(1+1/a)ª=e

a→∞

Число е (число Эйлера, неперово число) играет важную роль в матанализе.

lim (1+a)¹’ª=e

a→0

21 Пусть имеется ф-ия y=f(x), определённая на (а; в), говорят что ф-ия имеет в т. х0∈(а; в) производную f ’(x0) если существует предел

lim (f(x)-f(x0))/(x-x0)

x→x0

Производной ф-ии y=f(x) в точке х0 называется предел отношения приращения ф-ии к приращению аргумента, когда приращение аргумента стремится к нулю.

Ф-ия имеющая производную в каждой точке интервала называется дифференцируемой на этом интервале.

Геометрический смысл производной: пр-ая f `(x0) есть угловой коэфф. (tg угла наклона) касательной, проведённой к кривой y=f(x) в точке х0 , k=f ‘(x0)

у=f ‘(x0)(x - x0)

Механический смысл производной: пр-ая пути по времени s ‘(t0) есть скорость точки в момент t0: V(t0)=s ‘(t0)

Определение для любой точки

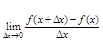
22 Производная алгебраической суммы конечного числа дифференцируемых ф-ий равна такой же сумме производных этих ф-ий

(u±v)`=u`± v`

Производная произведения двух дифференцируемых ф-ий равна произведению пр-ой первого сомножителя на второй плюс произведение первого сомножителя на про-ую второго:

(uv)`=u`v + uv`

Постоянный множитель можно выносить за знак

производной

(cu)`=cu`

Производная произведения нескольких

дифференцируемых ф-ий равна сумме произведений

производной каждого из сомножителей на все остальные

(uvw)`=u`vw+uv`w+uvw`

23 Производная частного двух ф-ий u(x)/v(x), если v(x)≠0

равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя есть квадрат прежнего знаменателя: (u/v)`=(u`v-uv`)/v²; v≠0

(u/c)`=1/c*u`

(c/u)`=-cv`/v² c=const

24 (xª)`=axªˉ¹

25 (LNx)`=1/x

(eª)`=eª

Для дифференцируемой ф-ии с производной, не равной

0, производная обратной ф-ии равна обратной величине

производной данной ф-ии

X`y = 1/Y`x

26 (sin x)`=cos x

(cos x)`=-sin x

(tg x)`=1/cos²x

(ctg x)`=-1/sin²x

27 Если y=f(u) и u=φ(x) – дифференцируемые ф-ии от своих аргументов, то производная сложной ф-ии существует и равна производной данной ф-ии по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по незавмсимой переменной х

y`=f`(u)*u`

y=f(u(x)) Fx`=Fu`*Ux`

Пример:

y=(√x+5)³ y`=?

y=u³, где u=√x+5

по формуле : y`=3u`*u`=3(√x+5)²(√x+5)`=3(√x+5)²/2√x

28 Дифференциалом ф-ии наз. линейная часть приращения ф-ии (относительно Δх), равная произведению производной на приращение независимой переменной.

dy=f`(x)Δx

Дифференциал независимой переменной равен приращению этой переменной.

Геометрический смысл: Дифференциал ф-ии есть приращение ординаты касательной, проведённой к графику ф-ии y=f(x) в данной точке когда х получает приращение Δх

29 При исследовании ф-ий используется следующий алгоритм:

1 ООФ, ОЗФ

2 Непрерывность ф-ии

3 Нахождение асимптот

4 Экстремумы и интервалы монотонности

5 Интервалы выпуклости и т. перегиба

6 Чётность нечётность, периодичность

7 Т. пересечения с Ох и Оу

(3)Если для некоторого х0 имеет место предел f(x) =∞ при

х→х0 то говорят, что х=х0 явл. вертикальн. асимптотой

f(x)

Если предел f(x)=b при x→∞ то говорят, что у=b явл.

горизонтальной асимптотой f(x)

Если предел f(x)/х=k при x→∞ (k≠0;k≠∞) и предел

(f(x)-kx)=b, то y=kx+b является наклонной асимпт-й

(4)Если производная ф-ии положительна (отрицательна)

внутри некоторого промежутка Х то ф-ия возрастает

(убывает) на этом промежутке

Если при переходе через т. х0 производная

дифференцируемой ф-ии меняет свой знак и в т. х0

равна 0 то х0-точка экстремума (минимума или

максимума)

(5)Точкой перегиба непрерывной ф-ии (f``(x)=0) наз. т. в

разделяющая интервалы, в которых ф-ия выпукла вниз и

вверх.

Ф-ия y=f(x) называется выпуклой внизу на интервале

(a;b) если f``(x)>0 на (a;b); ф-ия называется выпуклой

вверх на (a;b) если f``(x)<0 на (a;b)

30 Асимптотой графика ф-ии y=f(x) называется прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к 0 при неограниченном удалении точки графика от начала координат.

Если для некоторого х0 имеет место предел f(x)=∞ при

х→х0 то говорят, что х=х0 явл. вертикальн. асимптотой

f(x). Вертикальные асимптоты следует искать в точках

разрыва ф-ии или на концах её ООФ (а; в) если аи в –

конечные числа

Если предел f(x)=b при x→∞ то говорят, что у=b явл.

горизонтальной асимптотой f(x)

Если предел f(x)/х=k при x→∞ (k≠0;k≠∞) и предел

(f(x)-kx)=b, то y=kx+b является наклонной асимпт-й

Наклонная асимптота как и горизонтальная может быть

правосторонней или левосторонней

31 Степенным рядом наз. ряд вида (1)∑ Bn*xª = b0+b1x+b2x²…+baxª+… это ряд в котором членами являются ф-ии, в частности степенные. Совокупность тех значений х, при которых степнной ряд сходится, называется областью сходимости степнного ряда.

Ряд (1) наз. абсолютно сходящимся рядом, если сходится ряд (2) ∑ | bn |*| x |ª

Т1. Если ряд (2) сходится, то сходится и ряд (1)

Т2. Для любого степ. ряда (1) сущ-ет такое неотрицат. число R≥0 что этот ряд сходится абсолютно при | x |<R и расходится при | x |>R; R – радиус сходимости ряда

Даламбер: lim | Bn+1 |/| Bn |<1 (n→∞) сходится

>1 (n→∞) расходится

32 Разложение ф-ий в ряд:

Если бесконечно дифференцируемая ф-ия f(x0)=a0

f`=A1+2A2(x-x0)+n*An(x-x0)ªˉ¹

f(x)=f(x0)+f1(x0)(x-x0)+…+fª(x0)(x-x0)ª/a!

Рядом Тейлора ф-ии f(x) в окрестности т. х0 называется степ. рядом отн. разности (х-х0)

Особенно часто используется разложение ф-ии в ряд по степеням х, при этом х0=0; f(x)=f(0)+f`(0)+f ª(0)/a!*xª

Ряд Маклорена – частный случай ряда Тейлора

eª=1+x+x²/2!+x³/3!+…+xª/a!+…

sin x=1+ x-x³/3+…+(-1)ª*(x²ªˉ¹)/(2a+1)!+…

cos x=1-x²/2!+x⁴/4!+…+(-1)ⁿ*x²ⁿ/(2n)!+…

ln(1+x)=x-x²/2+x³/3-…+(-1)ⁿxⁿ⁺¹/n+1…

33 Ф-ия F(x) наз. первообразной для ф-ии f(x) если для всех х (из области определения) имеет место F`(x)≡f(x) нетрудно увидеть что если F(x) является первообразной для f(x) то и для F(x)+C также явл. первообразной.

Общий вид первообразной F(x)+C называется неопределённым интегралом от ф-ии f(x) обозначается F(x)+C=∫f(x)dx

dF(x)=F`(x)dx=f(x)dx

Св-ва неопр.∫

∫dF(x)=F(x)+C

(∫f(x)dx)`=f(x)

∫αf(x)dx=α∫f(x)dx

∫(f(x)±g(x))dx=∫f(x)dx±∫g(x)dx

Таблица интегралов

34 Метод замены переменных:

∫f(x)dx=∫f(φ(t))·φ`(t)dt → x=φ(t)

∫sin 5x dx=∫sin t 1/5dt=1/5∫sin t dt=-1/5 cost+C =-1/5cos 5x+C

5x=t; x=1/5t; dx=1/5 dt

35 Интегрир-ие по частям:

∫ U·dV=UV-∫VdU

Возможности применения связаны с тем, что дифференцир-ие может существенно упростить один из сомножителей (при условии что дифф-ие не слишком усложнит другой)

∫ x²·sinx dx

x²=U dU=2x dx

sin x dx =dV V=-cos x

∫ = x²·sin x dx=-x²·cos x -∫(-cos x)2x dx=-x²·cos x+2∫x·cos x dx

x=U dU=dx

cos x dx=dV V=sin x

∫ = x²·sin x dx=-x²cos x +2(x·sin x-∫sin x dx)= -x²·cos x+2x·sin x +2cos x+C

36 Рациональной дробью называется ф-ия, равная отношению двух многочленов f(x)=Pm(x)/Qn(x), Pm(x)-многочлен степени m, Qn(x)- многочлен степени n.

Рациональная дробь наз. правильной если степень числителя меньше степени знаменателя, т.е. m<n, в противном случае дробь неправильная.

Интегрирование дробей методом разложения на элементарные дроби:

1 Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби.

2 Разложив знаменатель дроби на множители, представить её в виде суммы простейших рац. дробей.

3 Проинтегрировать многочлен и полученную сумму простейших дробей.

37 Определённым интегралом от ф-ии f(x) на отрезке (a; b) называется предел интегральной суммы Sn, когда n→∞ (Δxi→0)

Cв-ва опр. интеграла:

(все интегралы на отрезке от А до В)

1 ∫С·f(x)dx=C·∫f(x)dx

2 ∫(f(x)±g(x))dx=∫f(x)dx±∫g(x)dx

3 ∫f(x)dx=-∫f(x)dx

4 Если f(x)≤g(x) на (A,B), то ∫f(x)dx≤∫g(x)dx

5 Если на (А,В) m=minf(x) M=maxf(x)то m(B-

-A)≤∫f(x)dx≤M(B-A)

6 Если f(x) непрерывна на (A,B) то сущ. также точка

С∈(A;B) ∫f(x)dx=f(C)·(B-A)

7 Если f(x) непрерывна на (А,В) то ∫f(x)dx существует

8 ∫f(x)dx=∫(a→d)f(x)dx+∫(d→b)f(x)dx

9 Формула Ньютона-Лейбница:

∫f(x)dx=F(B)-F(A)→F`(x)=f(x)

38 Применение опр. ∫

1 Вычисление площадей (Н-Лейб)

Если на (А,В) f(x)>0 то S=∫f(x)dx

Если на (А,В) f(x)<0 то S=-∫f(x)dx

Если на (А,В) f(x)>g(x) то S=∫[f(x)-g(x)]dx

(действительно для всех вариантов расп. ф-ий)

2 Вычисление объёмов тел вращения

V=π∫f²(x)dx

39 Приближ. вычисление интегралов

1 Формула Н-Лейб.

2 Метод прямоугольника

(B-A)/n=h: ∫(A→B)f(x)dx~=h(f1+f2…+fn)

3 Формула трапеции ∫f(x)dx~=h(1/2·f0+f1+f2+…fn)

4 Формула Симпсона

n-чётное

∫f(x(dx=(B-A)/3n(f0+4f1+2f2+4f3+2f4+…+4fn-1+fn)

40 Несобственные ∫ бывают 2-х видов:

∫-ы вида ∫(a;+∞)f(x)dx; ∫(-∞;b)f(x)dx; ∫(-∞;+∞)f(x)dx

называются несобственными ∫-и 1-го рода

Если сущ. предел (b→∞) ∫(a;b)f(x)dx=C (C≠∞) то интеграл сходится и наоборот.

Пусть есть числовой ряд ∑Ax=A0+A1+…An+… и пусть есть ф-ия f(x)=Ax на интервале [ a:b) Тогда ряд и несобственный ∫(a;∞)f(x)dx сходятся или расходятся одновременно

Если lim (x→b)f(x)=∞ или lim(x→a)f(x)=∞ то ∫f(x)dx наз. несобственным интегралом 2-го рода, он сходится если сущ. конечный предел

lim ∫(a; b-δ)f(x)dx

δ→0

41 Пусть имеется n переменных величин, и каждому набору их значений (x1,x2,x3…xn) из некоторого мн-ва Х соответствует одно вполне определённое значение переменной величины Z. Тогда говорят,что задана ф-ия нескольких переменных Z=f(x1…xn)

Если сущ-ет lim(Δx→0)f(x+Δx,y)-f(x,y)/Δx=fx`(x,y) то он называется частной производной по переменной х.

Если сущ-ет lim(Δy→0)f(x,y+Δy)-f(x,y)/Δy=fy`(x,y) то он называется частной производной по переменной y

Величина dZ=f`x(x;y)dx+f`y(x;y)dy называется дифференциалом от ф-ии f(x;y)

Z=f(x1+x2+…xn)dZ=f`x1·dx1+f`x2·dx2+…+f`xn·dxn

Дифференциалом ф-ии называется сумма произведений частных производных на приращение соответствующих независимых переменных.

42 Если Z=f(x;y) имеет в точке (х0;у0) экстремум (локальный) и ф-ия дифференцируема (т.е. имеет частные произв-ые) то частные произв-ые в этой т. равны 0.

43 Формулы служащие для аналитического представления опытных данных получили название эмпирических формул

Этапы вывода ЭФ:

1 Установить вид зависимости (линейная, квадратичная, логарифмическая и т.д.)

2 Определение известных параметров этой ф-ии

Для линейной зависимости сущ-ет метод наименьших

квадратов

44 ДУ называют ур-ие, связывающее искомую ф-ию одной или нескольких переменных, эти переменные, и производные различных порядков данной ф-ии.

Решением ДУ называется такая ф-ия, котю при подстановке её в это ур-ие обращает его в тождество.

ДУ первого порядка наз. ур-ие содержащее переменную х, неизвестную ф-ию y=f(x) и её производную y`=f`(x)

ДУ первого порядка наз. ур-ем с разделяющимися переменными, если оно м/б представленно в виде

dy/dx=f(x)g(y)

Для решения такого ур-ия его следует преобразовать к виду, в котором дифференциал и ф-ии переменной х окажутся в одной части равенства, а переменной у – в другой. Затем проинтегрировать обе части полученного рав-ва:

dy/g(y)=f(x)·dx → ∫ dy/g(y)=∫ f(x)·dx

f(x)	f`(x)	f(x)	f`(x)
c	0	xª	axªˉ¹
x	1	x²	2x
√x	2√x	arccos x	-1/√1-x² |x|<1
1/x	-1/x²	arctg x	1/1+x²
eⁿ	eⁿ	arcctg x	-1/1+x²
aⁿ	aⁿln a	sh x	ch x
ln x	1/x	ch x	sh x
LOGaX	1/x·ln a	th x	1/ch²x
sin x	cos x	cth x	-1/sh²x
cos x	-sinx	ln(x+√(x²+1))	1/√(1+x²)
tg x	1/cos²x	arcsin x	1/√(1-x²)
ctg x	-1/sin²x

f(x)	F(x)+C
0	C
1	x+C
x	x²/2+C
xª	xª⁺¹/a+1+C a≠1
1/x	ln| x |+C
1/x²	-1/x+C
1/x³	1/2x²+C
1/(1+x²)	arctg x+C
1/a²+x²	1/a·arctg x/a+C a≠0
1/1-x²	1/2·ln| (1+x)/(1-x) |+C
1/a²-x²	1/2a·ln| (a+x)/(a-x) |+C a≠0
x/x²+a	1/2·ln| x²+a |+C
1/√(1-x²)	arcsin x+C
1/√(a²-x²)	arcsin x/a+C
eⁿ	eⁿ
aⁿ	aⁿ/ln a
ln x	x ln x –x +C
sin x	-cos x+C
cos x	sin x+C
tg x	-ln | cos x |+C
ctg x	ln | sin x |+C
1/cos²x	tg x+C
1/sin²x	-ctg x+C

1. Понятие числа (от натур. до комплексного)

2. Сложение, вычитание, *, / для комплексного числа

3. Тригонометрическая форма комплексного числа

4. Возведение в степень комплексного числа

5. Извлечение ªÖ из комплексного числа

6. Последовательность и её предел

7. Св-во сходящихся последовательностей (док-во)

8. БМВ и ограниченная последовательность. Св-ва БМВ

9. Знакоположительный ряд и его сходимость (пример)

10. Признак сравнения двух знакоположительных рядов (примеры)

11. Признаки Даламбера и Коши

12. Знакопеременный ряд. Признак Лейбница (пример)

13. Прямая и обратная функция (примеры)

14. Предел ф-ии в точке

15. Непрерывность ф-ии в точке. Св-ва непрерывных ф-ий

16. Непрерывность линейной и степенной ф-ий

17. Непрерывность ф-ий Вª и LOGaX

18. Непрерывность тригонометрической ф-ии

19. 1-ый замечательный предел

20. 2-ой замечательный предел и его применение для

начисления непрерывных %

21. Понятие производной от ф-ии. Геометрический и механический

смысл призводной

22. Понятие пр-ой. Пр-ая от +, -, * двух ф-ий

23. Понятие пр-ой. Пр-ая от / двух ф-ий

24. Понятие пр-ой. Пр-ая от Хª

25. Понятие пр-ой. Пр-ая от обратных ф-ий (LNx, eª)

26. Пр-ая от тригонометрической ф-ии.

27. Пр-ая от сложной ф-ии (пример)

28. Понятие дифференциала ф-ии. Его геометр. смысл

29. Исследование ф-ий с помощью пр-ой и пределов.

30. Понятие асимптот и их нахождение

31. Степенной ряд и область его сходимости

32. Разложение ф-ий в степенные ряды

33. Неопределённый интеграл. Табл. Интегралов

34. Метод интегрир-ия с помощью замены переменных (примеры)

35. Интегрирование по частям

36. Интегрир-ие с помощью разложения на элементарнве дроби

37. Определённый интеграл и его св-ва. Формула Ньютона-Лейбница

38. Применение опр. интегралов

39. Приближённый метод вычисления опр. интегралов

40. Несобственные интегралы

41. Ф-ии нескольких переменных. Понятие частных пр-ых и дифференциала

42. Экстремум ф-ий нескольких переменных

43. Понятие об эмпирических формулах. Метод наименьших квадратов.

44 Понятие ДУ и методы его решения.