Чтение и запись натуральных чисел

Г. Самойлик, методист ОМЦ ЗОУКО, Москва

На уроке по теме «Обозначение натуральных чисел» учителю непременно понадобится следующий материал.

Для счета предметов применяют натуральные числа. Любое натуральное число можно записать с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Эти цифры иногда по ошибке называют «арабскими». Дело в том, что индийскую систему нумерации усвоили арабы, а труды индийских ученых в Европе стали известны значительно позже, чем труды арабских ученых. Поэтому эти ци

фры правильнее называть индийскими. Наш способ счета и записи чисел называется Для счета предметов применяют натуральные числа. Любое натуральное число можно записать с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Эти цифры иногда по ошибке называют «арабскими». Для счета предметов применяют натуральные числа. Любое натуральное число можно записать с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Эти цифры иногда по ошибке называют «арабскими». а в Индии около 2000 лет назад. В Европе она распространилась благодаря труду по арифметике среднеазиатского ученого Мухаммеда Хорезми (ал-Хорезми) (780–850 гг.).

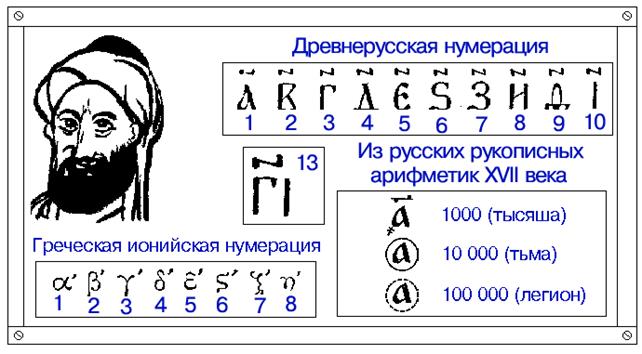
Одним из древнейших трудов по арифметике, дошедших до нас, является учебник «Вопросы и решения» армянского философа и математика Анания Ширакаци, жившего в VII в. В его книге применяется алфавитная нумерация. Десятичная алфавитная нумерация была распространена и в Киевской Руси. В древности на Руси писали числа при помощи букв славянского алфавита, над которым ставили особый значок – титло (~).

Учитель, готовый украсить свой урок, перед его началом должен иметь на доске красочные плакаты (естественно, закрытые от глаз учеников до поры до времени либо занавесками, либо газетами. Это очень важный и эффективный методический прием, который следует иметь в виду учителю. Плакаты нужно обязательно закрыть, иначе ученики растеряют свое внимание перед уроком и затем собрать их внимание учителю будет не под силу. (Поэтому всегда, особенно в 5-м классе, следует закрывать наглядный материал, помещенный на доске). На доску может быть вынесен следующий материал.

Что касается старинных задач к этой теме, то таковых можно предложить множество. Можно, например, воспользоваться сборником «Старинные занимательные задачи» автора С.Н. Олехника, вышедшим в издательстве «Наука» в 1988 г.

Приведу здесь лишь некоторые примеры таких задач.

1. Величайший математик древности Архимед погиб в возрасте 75 лет во время осады Сиракуз (212 г. до н. э.). Определите год рождения Архимеда.

[212 + 75 = 287 г. до н. э.]

2. Зная содержание предыдудщей задачи, определите, сколько лет назад родился Архимед.

[2002 + 287 = 2289 лет.]

Задачи из старинных русских рукописей

3. На охоте

Пошел охотник на охоту с собакой. Идут они лесом, и вдруг собака увидела зайца. За сколько скачков собака догонит зайца, если расстояние от собаки до зайца равно 40 скачкам собаки и расстояние, которое пробегает собака за 5 скачков, заяц пробегает за 6 скачков? (В задаче подразумевается, что скачки делаются одновременно и зайцем, и собакой.)

Решение. Если заяц сделает 6 скачков, то и собака сделает 6 скачков, но собака за 5 скачков из 6 пробегает то же расстояние, что и заяц за 6 скачков. Следовательно, за 6 скачков собака приблизится к зайцу на расстояние, равное одному своему скачку. Поскольку в начальный момент расстояние между зайцем и собакой было равно 40 скачкам собаки, то собака догонит зайца через 40ж6 =

= 240 скачков.

4. Воз сена

Лошадь съедает воз сена за месяц, коза за два месяца, овца за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?

Решение. Поскольку лошадь съедает воз сена за месяц, то за год (12 месяцев) она съест 12 возов сена. Так как коза съедает воз сена за два месяца, то за год она съест 6 возов сена. И наконец, поскольку овца съедает воз сена за 3 месяца, то за год она съест 4 воза сена. Вместе же они съедят за год 12 + 6 + 4 = 22 воза сена. Тогда один воз сена они все вместе съедят за месяца.

Особенностью подачи исторического материала в 5-м классе является незагруженность его слишком сложными и объемными сведениями, его лаконичность, четкость и красочность, иллюстрирующего его материала.