Название: Вычисление пределов функций, производных и интегралов

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 78.81 Kb

Скачать файл: referat.me-217704.docx

Краткое описание работы: Изучение способов нахождения пределов функций и их производных. Правило дифференцирования сложных функций. Исследование поведения функции на концах заданных промежутков. Вычисление площади фигуры при помощи интегралов. Решение дифференциальных уравнений.

Вычисление пределов функций, производных и интегралов

Содержание

Задание № 1

Задание № 2

Задание № 3

Задание № 4

Задание № 5

Задание № 7

Задание № 8

Задача № 4

Задача № 5

Задача № 6

Список литературы

Задание № 1

3. б) Найти пределы функции:

Решение

Одна из основных теорем, на которой основано вычисление пределов:

Если существуют

и , то:

Следовательно:

Ответ: предел функции

Задание № 2

3. б) Найти производную функции:

Решение

Воспользуемся правилом дифференцирования сложных функций:

Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.

Тогда

Применим это правило к заданной функции:

Ответ:

Задание № 3

3. Исследовать функцию и построить ее график:

Решение

1. Найдем область определения функции:

D(y)=R

2. Исследуем функцию на четность и нечетность, на периодичность.

Условие четности: f(x)=f(-x)

Условие нечетности: f(-x)=-f(x)

при x=1: y=0

при x=-1: y=-4

Условия не выполняются, следовательно, функция не является четной и нечетной.

Периодической называется такая функция, значения которой не изменяются при прибавлении к аргументу некоторого (отличного от нуля) числа – периода функции.

Функция

не периодична.

3. Найдем промежутки знакопостоянства, выясним поведение функции на концах промежутков.

y=0 при

;

Следовательно, имеем три промежутка:

Определим знак на каждом промежутке:

при x= -1 y=-4 < 0

при x= 0,5 y=0,125 > 0

при x= 2 y=2 > 0

Тогда: для

, для

Рассмотрим поведение функции на концах промежутков:

4. Найдем промежутки монотонности функции, ее экстремумы.

Найдем производную функции:

при

,

- точки экстремума, они делят область определения функции на три промежутка:

Исследуемая функция в промежутке

– возрастает

– убывает

- возрастает

5. Найдем промежутки выпуклости графика функции, ее точки перегиба.

Найдем вторую производную функции:

при - точка перегиба

Для

,

следовательно, график функции на этом интервале выпуклый вверх.

Для

,

следовательно, график функции на этом интервале выпуклый вниз.

6. По полученным данным построим график функции.

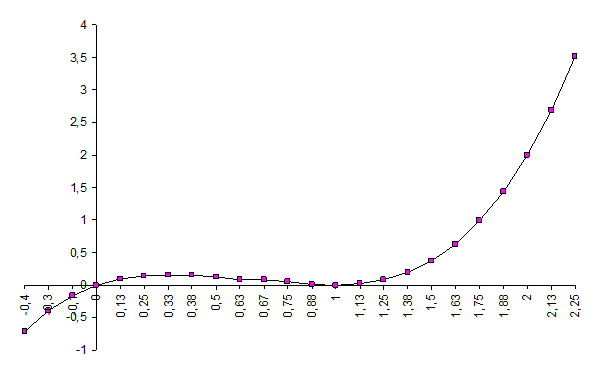
Рис. 3 График функции

Задание № 4

Найти интеграл:

3.

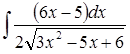
Решение

Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:

F(x) + C.

Записывают:

Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.

Замена переменной в неопределенном интеграле производится с помощью подстановки:

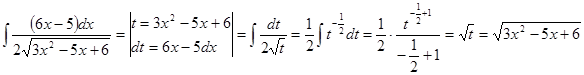
Ответ: .

Задание № 5

Вычислить площадь фигуры, ограниченной линиями, используя определенный интеграл. Сделать чертеж.

, , , .

Решение.

Построим график функции:

при х=-2: y = 12

при х=-1: y = 5

при х=0: y = 0

при х=1: y = -3

при х=2: y = -4

при х=3: y = -3

при х=4: y = 0

при х=5: y = 5

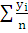
Рис. 1 График

Найдем точки пересечения графика функции с осью Оx:

Определим площадь полученной фигуры через определенный интеграл:

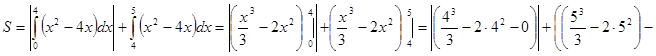
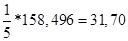кв. ед.

Ответ: площадь фигуры, ограниченной заданными линиями = 13 кв. ед.

Задание № 7.

Найти общее решение или общий интеграл дифференциального уравнения, решить задачу Коши для заданных начальных условий:

, при

Решение

Общий вид дифференциального уравнения:

Общим решением дифференциального уравнения первого порядка называется функция от переменной x и произвольной постоянной C, обращающая уравнение в тождество. Общее решение, записанное в неявном виде , называется общим интегралом.

Решение, полученное из общего при фиксированном значении С: , где - фиксированное число, полученное при заданных начальных условиях , называется частным решением, или решением задач Коши .

Найдем общее решение или общий интеграл:

-

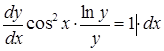
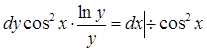
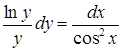
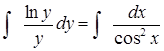
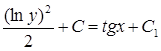
общее решение дифференциального уравнения

Найдем частное решение для при

Получаем:

Ответ: - любое число.

Задание № 8

Найти вероятность случайного события.

Условие: Брошена игральная кость. Какова вероятность того, что выпадет нечетное число очков? Что выпадет шестерка»?

Решение.

Вероятностью события А называется математическая оценка возможности появления этого события в результате опыта. Вероятность события А равна отношению числа, благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий.

..................................................................................................................

Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А.

Обозначим в данной задаче выпадение нечетного числа – событие А, выпадение «шестерки» – событие В. На игральной кости шесть граней, очевидно, что на трех из них число нечетное, на одной – «шестерка».

Тогда в соответствии с записанными выше формулами получаем:

.

Ответ: 1. вероятность выпадения нечетного числа равна ;

2. вероятность выпадения «шестерки» равна .

Методы вычислений и ЭВМ

Задача № 4.

Внедрение автоматизированного способа обработки информации снизило расходы на ее обработку с 238200 руб. до 50175 руб. Определите, на сколько процентов снизились расходы на обработку информации. Приведите рациональный алгоритм вычислений на МК.

Решение:

Схема решения	Алгоритм	Результат
238200 – 100 % 50175 – х %		21,064 %

Задача № 5

Расходы на перевозку почты во II квартале уменьшились на 2,5 % по сравнению с I кварталом; в III квартале увеличились на 2,9 % по сравнению со II кварталом; IV квартале они вновь увеличились на 3,1 % по сравнению с III кварталом. Определите с точностью до 0,1 %, как изменились расходы в IV квартале по сравнению с I кварталом. Запишите рациональный алгоритм вычислений на МК.

Решение:

По условию задачи задано последовательное изменение начального показателя N=100 процентов на

Р1=2,5 %, Р2=2,9 %, Р3= 3,1 %.

Тогда:

Nn = 100(1-2,5/100)(1+2,9/100)(1+3,1/100) = 100(1-0,025)(1+0,029)(1+0,031) = 100*0,975*1,029*1,031 = 103,4 %

Алгоритм выполнения этого вычисления на МК:

100 – 2,5 % + 2,9 % + 3,1 %

Задача № 6

Бригаде монтажников за месяц начислено 16713 руб. Распределите заработную плату между членами бригады пропорционально следующим данным. Приведите рациональный алгоритм вычислений на МК, а также решение задачи с помощью табличного процессора (Excel, Super Calc и др.). Точность 0,01 руб.

Табельный номер	Часовая тарифная ставка, руб	Отработано часов	К оплате, руб
03	6,6	165
04	8,8	72
05	7,5	216

Алгоритм решения на МК:

6,6 * 165 М+

8,8 * 72 М+

7,5 * 216 М+

_{16713 / MR MR} * 1089 = М+

^{C C} 633,6 = М+

1620 = М+ _MR

^C

Решение задачи с помощью табличного процессора Excel:

1. Ввод названий граф документа:

Адрес клетки	Вводимая строка
А1	Табельный номер
А2	03
А3	04
А4	05
В1	Начислено, руб. (всего)
С1	Часовая тарифная ставка, руб.
D1	Отработано часов
Е1	К оплате, руб.

2. Ввод исходных данных:

Адрес ячейки	Исходные данные
В2	16713
С2	6,6
С3	8,8
С4	7,5
D2	165
D3	72
D4	216

3. Ввод расчетных формул:

Адрес ячейки	Исходные данные
F2	С2*D2
F5	=СУММ(F2:F4)
E2	$B$2/$F$5*F2
E5	=СУММ(Е2:Е4)

4. Конечный результат:

Табельный номер	Начислено, руб. (всего)	Часовая тарифная ставка, руб.	Отработано часов, ч.	К оплате, руб.	Ставка, руб.
03	16713	6,6	165	5445,00	1089,00
04		8,8	72	3168,00	633,60
05		7,5	216	8100,00	1620,00
				16713,00	3342,60

Список литературы

1. Выгодский М.Я. Справочник по высшей математике. – М.: АСТ, 2005. – 991 с.

2. Гусак А.А., Гусак Г.М., Бричкова Е.А. Справочник по высшей математике. – Минск. ТетраСистемс, 2004. – 640 с.

3. Гмурман В.Е. Теория вероятности и математическая статистика. – М.: Высшая школа, 1998. – 479 с.

4. Миносцев В.Б. Курс высшей математики. Часть 2. М. 2005. – 517 с.

5. Пономарев К.К. Курс высшей математики. Ч. 2. – М.: Инфра-С, 1974. – 520 с.