Referat.me
/ / Математический анализ

Название: Математический анализ

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 141.25 Kb

Скачать файл: referat.me-218872.docx

Краткое описание работы: Исследование заданной функции и построение ее графика. Расчет объема тела, полученного вращением вокруг оси абсцисс фигуры, ограниченной линиями и осями координат. Вычисление интеграла при заданной силе. Работа, которую нужно совершить для сжатия пружины.

Математический анализ

Оглавление

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Задание 6

Литература


Задание 1.

Исследовать функцию и построить ее график: .

Решение:

y = 0, если х = 0 или х =

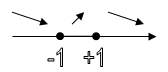
y(-1) = -2, y(1) = 2.


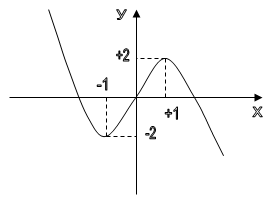
Задание 2

1. ;

2. ;

3. ;

4. ;

5. Найти dy, если .

Решение:

1.

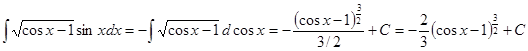
2.

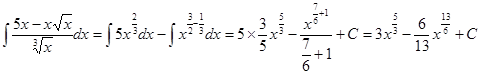
3.

4.

5. ,

Ответ: 1. ; 2. ; 3. ; 4. ; 5. .


Задание 3.

Вычислить объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линиями , х = 3 и осями координат.

Решение:

.

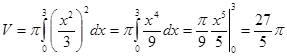Ответ:.

Задание 4.

Для сжатия пружины на L см требуется сила 9,8 Н. Какую работу надо совершить, чтобы сжать пружину на 0,05 м.

Решение:

Работа , где F – сила, s – расстояние, пройденное под действием этой силы.

По закону Гука , где - абсолютное удлинение стержня, F – сила упругости, k – жесткость материала. Следовательно,

.

Ответ: .

Задание 5.

Найти интеграл:

а) 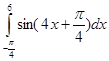;б) .

Решение:

а)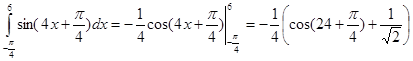

б) .

Ответ: а) ; б) .


Задание 6.

Исследовать функцию и построить ее график:

1. ;

2. ;

3. ;

4. ;

5.

Решение:

1. - симметрична относительно оси Ох

y = 0, если 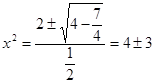, т.е. .

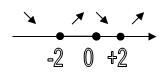
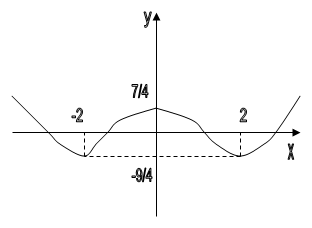
y(-2) = y(2) = -9/4

y(0) = 7/4


2.

Область определения

y = 0, если , корней нет:

, если


Корень один, он близок к х = 1, находится между х = 1,05 и х = 1,06, это точка минимума.

y(1) = 2, y(2) = 3.2, y(3) = 4,95

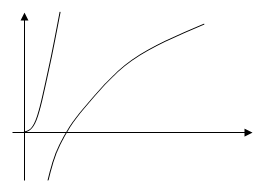
3.

y = 0, если х = 1,

область определения ,


, х = 0 – асимптота.

;

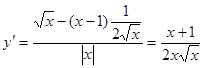корней, принадлежащих области определения, нет.

;

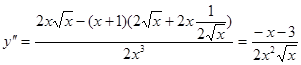корней, принадлежащих области определения, нет.

4.

Уравнение y = 0 корней не имеет,


, , х = 1/5 – асимптота

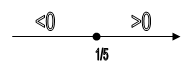
y(0.007) = -0.3

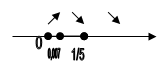
5.

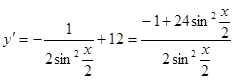
y(0.4 + 4πk) = 4.9 + 48πk

y(-0.4 + 4πk) = -4.9 + 48πk

,

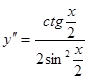знак совпадает со знаком ctg(x/2)


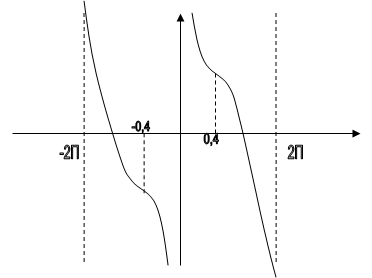
Литература

1. Зорич В.А. Математический анализ. Ч. 1, М., 2001. Ч. 2. 2001.

2. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч. 1. М., 2001. Ч. 2, М., 2002.

3. Кудрявцев Л.Д. Курс математического анализа: В 3 т. М., 1988-1989.

4. Камынин Л.И. Курс математического анализа. Т. 1. М., 1993. Т. 2. М., 1995.

5. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М., 2003.

Похожие работы

  • Вычисление интегралов

    Методика и основные этапы нахождения параметров: площади криволинейной трапеции и сектора, длины дуги кривой, объема тел, площади поверхности тел вращения, работы переменной силы. Порядок и механизм вычисления интегралов с помощью пакета MathCAD.

  • Формулы по математическому анализу

    Формулы дифференцирования Таблица основных интегралов Правила интегрирования Основные правила дифференцирования Пусть С—постоянная, u=u(x), v=v(x) – функции, имеющие

  • Система уравнений по формулам Крамера

    Задание № 1 Решить систему уравнений: 1) по формулам Крамера 2) с помощью обратной матрицы 3) методом Гаусса Решение найдем определитель матрицы 1) методом Крамера

  • Приближенный метод решения интегралов. Метод прямоугольников (правых, средних, левых)

    Лабораторная работа № 4. Приближенный метод решения интегралов. Метод прямоугольников (правых, средних, левых). Гребенникова Марина 12-А класс Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида

  • Вычисление координат центра тяжести плоской фигуры

    Министерство общего и профессионального образования Российской федерации. Уральский Государственный Технический Университет - УПИ. Реферат ВЫЧИСЛЕНИЕ КООРДИНАТ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ.

  • Функционально-графический подход к решению задач с параметрами

    Выполнение алгебраических преобразований, логическая культура и техника исследования. Основные типы задач с параметрами, нахождение количества решений в зависимости от значения параметра. Основные методы решения задач, методы построения графиков функций.

  • Интегралы, объем тела вращения, метод наименьших квадратов

    Неопределенный интеграл. Объем тела вращения. Эмпирическая формула. Сходимость ряда. Вычисление объема тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями. Исследование на условную сходимость по признаку Лейбница.

  • Дифференциальные уравнения

    Вычисление первого и второго замечательных пределов, неопределенного и определенного интегралов, площади криволинейной трапеции, координат середин сторон треугольника с заданными вершинами. Определение критических точек и асимптот графика функции.

  • Геометрические и физические приложения двойных, тройных, криволинейных и поверхностных интеграло

    СОДЕРЖАНИЕ 1.Геометрические приложения интегралов 1.1 Геометрические приложения двойных интегралов………….. 3 1.2 Геометрические приложения тройных интегралов………….. 5

  • Задачи на наибольшее и наименьшее значения функций

    Задачи на наибольшее и наименьшее значения функции Требуется изготовить коническую воронку с образующей l=10см. Каков должен быть радиус основания воронки, чтобы ее объем был наибольшим?