Referat.me
/ / Система уравнений по формулам Крамера

Название: Система уравнений по формулам Крамера

Вид работы: реферат

Рубрика: Математика

Размер файла: 160.17 Kb

Скачать файл: referat.me-218032.docx

Краткое описание работы: Задание № 1 Решить систему уравнений: 1) по формулам Крамера 2) с помощью обратной матрицы 3) методом Гаусса Решение найдем определитель матрицы 1) методом Крамера

Система уравнений по формулам Крамера

Задание № 1

Решить систему уравнений:

1) по формулам Крамера

2) с помощью обратной матрицы

3) методом Гаусса

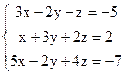
Решение

найдем определитель матрицы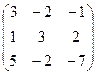

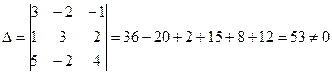
1) методом Крамера

найдем определители

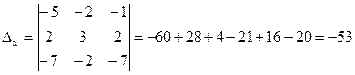
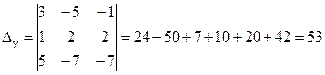
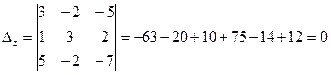
найдем значения ; ;

2) метод обратной матрицы

транспонированная матрица

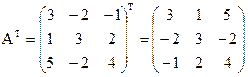
найдем алгебраические дополнения

; ; ;

; ; ;

; ; ;

матрица из дополнений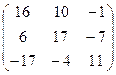

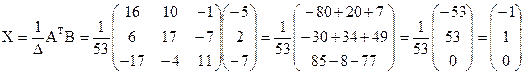
3) методом Гаусса

построим расширенную матрицу

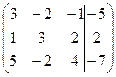
приведем матрицу к треугольному виду

разделим первое уравнение на 3 и вычтем второе

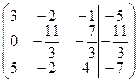
умножим первое уравнение на 5/3 вычтем третье

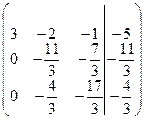
Второе уравнение умножим на 3, третье уравнение умножим на 3

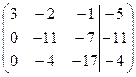
второе уравнение умножаем на 4/11 вычитаем третье.

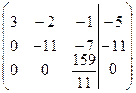
Первое уравнение разделим на 3

Второе уравнение разделим на -11

третье уравнение разделим на 159/11

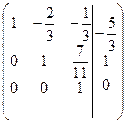
полученной матрице соответствует система уравнений

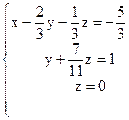
решаем уравнение снизу вверх

решение системы

Задание № 2

Координаты вершин пирамиды А(1, -4, 0), В(5, 0, -2), С(3, 7, -10), Д(1, -2, 1) – вершины пирамиды. Найти:

1) записать векторы АВ, АС, АД в системе орт и найти их длины

2) найти угол между векторами АВ и АС

3) найти проекцию вектора АД на вектор АВ

4) найти площадь грани АВС

5) найти объем пирамиды АВСД

Решение

1. записать векторы в системе орт и найти их длины.

Произвольный вектор может быть представлен в системе орт i, j, k следующей формулой , где - проекции вектора а на соответствующие координатные оси. Если даны точки и , то проекции вектора на координатные оси находятся по формулам

; ;

расстояние между двумя точками и определяется по формуле

запишем вектор

; ; ;

длина АВ будет равна

запишем вектор

; ; ;

длина АС будет равна

запишем вектор

; ; ;

длина АД будет равна

2. найти угол между векторами ;

косинус угла между двумя векторами равен скалярному произведению этих векторов, деленному на произведение их модулей.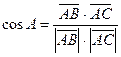

модуль вектора равен

модуль вектора равен

скалярное произведение векторов

Таким образом, , угол А=36,86°

3. найти проекцию вектора на вектор ;

Проекция вектора на вектор равна скалярному произведению этих векторов, деленному на модуль вектора

скалярное произведение векторов

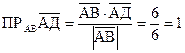
4. найти объем пирамиды ABCД

Объем пирамиды равен 1/6 объема параллелепипеда, построенного на ребрах

Объем параллелепипеда, построенного на трех некомпланарных векторах , , , равен абсолютной величине их смешанного произведения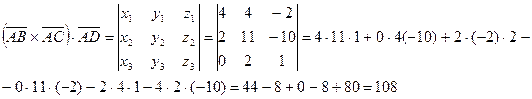

Объем пирамиды равен

Задание № 3

Найти указанные пределы

а)

б)

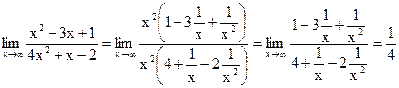
- бесконечно малые

в)

tgα(x)~α(x) эквивалентные бесконечно малые при α(x)→0

г)

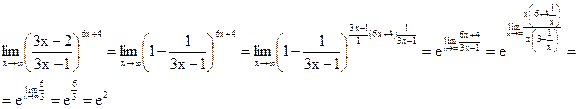
- бесконечно малые

Задание № 4

Найти производные функции

а)

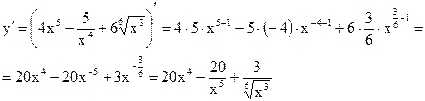
б)

в)

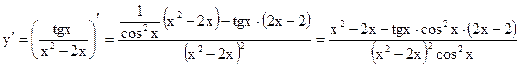
г)

д)

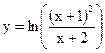
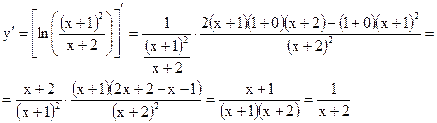
Задание № 5

Найти производную указанного порядка

Задание № 6

Найти дифференциал функции

Задание № 7

Найти неопределенные интегралы и результат проверить дифееренцированием

а)

проверка

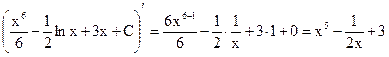
б)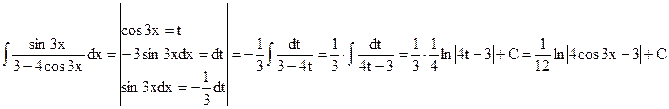

проверка

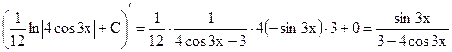
в)

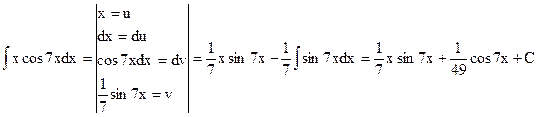
проверка

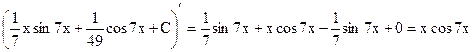
Задание № 8

Найти площадь фигуры, ограниченной линиями. Сделать схематический чертеж

Вычислить объем тела, образованного вращением вокруг оси ох фигуры, ограниченной указанными линиями. Сделать схематический чертеж

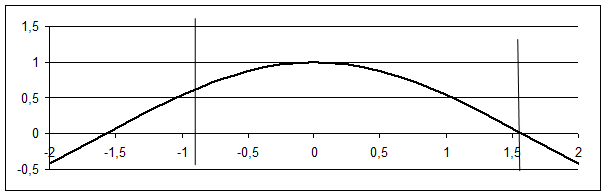
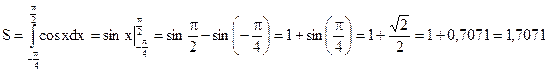
Объем фигуры образованной вращением вокруг оси ох ограниченной линиями

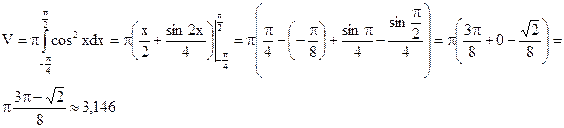
Похожие работы

  • Системы линейных уравнений и неравенств

    Основные понятия теории систем уравнений. Метод Гаусса — метод последовательного исключения переменных. Формулы Крамера. Решение систем линейных уравнений методом обратной матрицы. Теорема Кронекер–Капелли. Совместность систем однородных уравнений.

  • Определитель матрицы 2

    Оглавление Задача 2 3 Задача 3 5 Задача 4 7 Задача 1 Вычислить определитель 4-го порядка. Решение: Определитель 4-го порядка находится по формуле: aij – элемент матрицы;

  • Алгебра матриц. Системы линейных уравнений

    Выполнение действий над матрицами. Определение обратной матрицы. Решение матричных уравнений и системы уравнений матричным способом, используя алгебраические дополнения. Исследование и решение системы линейных уравнений методом Крамера и Гаусса.

  • Метод Крамера

    Министерство рыбного хозяйства Владивостокский морской колледж ТЕМА: “ Системы 2-х , 3-х линейных уравнений. Правило Крамера. ” г. Владивосток

  • Матричная форма формулы Крамера

    С.К. Соболев Матричный способ решения СЛАУ, формулы Крамера, свойство присоединенной матрицы и основное свойство линейной зависимости. Рассмотрим

  • Основы высшей матиматики

    Вычисление определителя 4-го порядка, математическое решение системы методами матрицы, Крамера и Гаусса. Характеристика понятий невырожденной и обратной, транспонированной и присоединенной матрицы, нахождение алгебраических дополнений элементов таблицы.

  • Задачи по Математике

    ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ Задачи № 1-10. Решить систему линейных алгебраических уравнений тремя способами: 1) методом Крамера, 2) с помощью обратной матрицы, 3) методом Гаусса.

  • Основы высшей математики

    Построение подмножеств и диаграмм Венна по заданному универсальному множеству и его составляющим. Сложение, вычитание и транспонирование матриц. Метод понижения порядка и приведения системы к треугольному виду. Методы Крамера, Гаусса и матричный способ.

  • Системы 2-х, 3-х линейных уравнений, правило Крамера

    Краткая теория. Методические рекомендации по выполнению заданий. Примеры выполнения заданий.

  • Системы линейных уравнений

    Критерий совместности. Метод Гаусса. Формулы Крамера. Матричный метод.