Название: Применение непрерывности и производной 11 класс

Вид работы: лабораторная работа

Рубрика: Математика

Размер файла: 28.43 Kb

Скачать файл: referat.me-216113.docx

Краткое описание работы: Лабораторная работа №1 Характеристики тестовых заданий План: Составление матрицы, приведение к треугольному виду, анализ неверных профилей, подсчет мер центральной тенденции, мер изменчивости, мер симметрии и островершинности кривой распределения.

Применение непрерывности и производной 11 класс

Лабораторная работа №1

Характеристики тестовых заданий

План:

1. Составление матрицы, приведение к треугольному виду, анализ неверных профилей, подсчет мер центральной тенденции, мер изменчивости, мер симметрии и островершинности кривой распределения.

2. Дистракторный анализ

3. Дифференцирующая способность тестового задания (метод крайних групп)

Задания выполняются в программе Microsoft Excel . Слушателям можно раздать распечатки хода выполнения работы (см. файл в приложениях Лабораторная работа01. doc )

1. Составление матрицы, приведение к треугольному виду, анализ неверных профилей, подсчет мер центральной тенденции, мер изменчивости, мер симметрии и островершинности кривой распределения.

Раздаточный материал: Отработанные бланки ответов, на тест. (Перед занятием необходимо было протестировать испытуемых по своему тесту).

Обозначения:

x_i – индивидуальный балл i – ого ученика,

- среднее значение баллов по тестируемой группе,

- стандартное отклонение,

N – число учеников,

n – число заданий в тесте.

Ход работы:

1) Заполнить матрицу результатов тестирования. (Использовать образец из файла Приложение1.xls).

2) Удалить все строки и столбцы, состоящие только из 1 или только из 0.

3) Подсчитать индивидуальные баллы испытуемых и количество правильных ответов испытуемых на каждое задание теста.

4) Привести матрицу к треугольному виду: для этого производят перестановку столбцов, располагая задания по убыванию числа правильных ответов на них. Затем сортируют строки по возрастанию индивидуальных баллов испытуемых.

5) Посчитать количество ошибок в каждом профиле ответов. (Преподаватель демонстрирует параллельно выполнение задания, используя файл с матрицей результатов тестирования, представленной в файле Приложение2.xls)

6) Найти для своих данных моду, среднее выборочное.

7) Добавить столбец, в котором вычисляется разность между индивидуальным баллом и средним выборочным.

8) Посчитать дисперсию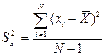

9) Посчитать стандартное отклонение , используя выражение сделать вывод о нормальности распределения.

10) Подсчитать:

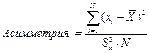
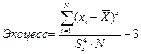
Сделать выводы.

11) На отдельном листе создать таблицу:

xi	Кол. испытуемых с индивидуальным баллом xi	Процент испытуемых с индивидуальным баллом xi
1
2
,,,
,,,
,,,
n

Построить гистограмму распределения индивидуальных баллов по последнему столбику (подписи к оси ОХ берем из 1 столбца).

12) Провести анализ полученной гистограммы.

2. Дистракторный анализ

Выполнить дистракторный анализ для своих данных по заданиям закрытой формы.

(В качестве примера см. файл Приложение3.xls)

Оценка правдоподобности дистракторов основана на подсчете долей испытуемых, выбравших каждый из неправильных ответов. Количество испытуемых, выбравших неверный ответ должно равномерно распределяться между дистракторами. Конечно на практике такая идеализированная ситуация редко встречается. Дистракторы, оказавшиеся неправдоподобными по результатам эмпирической проверки необходимо заменить.

Заполнить таблицу по своим данным и сделать выводы о качестве дистракторов. Первый столбец содержит номера заданий. Второй – указывает количество испытуемых, выполнявших данное задание. Если испытуемый не приступал к выполнению задания, то он не учитывается (например в заданиях №5 и №10). Все последующие столбцы содержат число и процент испытуемых, выбравших каждый из ответов к заданиям теста. Звездочкой отмечен верный ответ на задание.

Анализ правдоподобности дистракторов
№	всего	Распределение ответов испытуемых
1-ый ответ		2-ый ответ		3-ый ответ		4-ый ответ
тест	%	тест	%	тест	%	тест	%
1	50	48*	96%	1	2%	1	2%	0	0%
2	50	4	8%	3	6%	2	4%	41*	82%
3	50	25*	50%	6	12%	15	30%	4	8%
4	50	7	14%	0	0%	10	20%	33*	66%
5	49	30*	61%	3	6%	7	14%	9	18%
6	50	20	40%	5	10%	17*	34%	8	16%
7	50	5	10%	9	18%	2	4%	34*	68%
8	50	31*	62%	6	12%	6	12%	7	14%
9	50	43*	86%	3	6%	2	4%	2	4%
10	48	9	19%	32*	67%	2	4%	5	10%

3. Дифференцирующая способность тестового задания (метод крайних групп)

Дискриминативностью (дифференцирующей способностью) называют способность тестового задания дифференцировать учеников на более или менее подготовленных. Так как основная цель нормативно-ориентированного теста – это достижение дифференцирующего эффекта, то высокий показатель дискриминативности очень важен для задания.

Для оценки дискриминативности задания будем использовать расчет по формуле:

, где - индекс дискриминативности для j-ого задания теста; (P₁ )_j – процент учеников, правильно выполнивших j-ое задание в подгруппе из 27% лучших учеников по результатам выполнения теста; (P₀ )_j – процент учеников, правильно выполнивших j-ое задание в подгруппе из 27% худших учеников по результатам выполнения теста.

Индекс дискриминативности изменяется в пределах [-1; 1]. Максимального значения он достигает в том случае, когда все ученики из подгруппы сильных верно выполняют данное задание, а из подгруппы слабых это задание не выполняет верно никто. В этом случае задание будет обладать максимальным дифференцирующим эффектом. Нулевого значения индекс дискриминативности достигает тогда, когда в обеих подгруппах доли учеников, справившихся с заданием равны. Соответственно дифференцирующего эффекта нет вообще. Значение меньше 0 будет в ситуации, когда данное задание теста слабые ученики выполняют успешнее, чем сильные. Естественно, что задания, у которых индекс дискриминативности равен или ниже нуля необходимо удалить из теста.

Используя данные из файла Приложение4.xls, посчитать индекс дискриминативности для каждого задания. Сделать выводы.