Referat.me
/ / Основы высшей математики

Название: Основы высшей математики

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 35.66 Kb

Скачать файл: referat.me-215220.docx

Краткое описание работы: Построение подмножеств и диаграмм Венна по заданному универсальному множеству и его составляющим. Сложение, вычитание и транспонирование матриц. Метод понижения порядка и приведения системы к треугольному виду. Методы Крамера, Гаусса и матричный способ.

Основы высшей математики

Задание 1

Задано универсальное множество U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} и его подмножества A = {1, 3, 5, 7, 9}, B = {2, 4, 6, 8, 10}, C = {1, 2, 3, 4, 5}

Найти указанные в таблице подмножества и построить диаграммы Венна.

С + АВ – ВТ

А =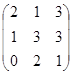

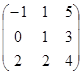
C = A x B

C11 = 2 x (-1) + (1 x 0) + 3 x 2 = -2 +6 = 4

C12 = 2 + 1 x1 +3 x 2 = 2+1 +6 = 9

C13 = 2 x 5 + 1 x 3 + 3 x 4 = 10 + 3 + 12 = 25

C21 = -1 x 1 + 3 x 0 + 3 x 2 = -1 + 6 = 5

C22 = 1 x 1+ 3 x1 +3 x 2 = 1 + 3 + 6 =10

C23 = 1 x 5 + 3 x 3+ 3 x 4 = 5 + 9 +12 = 14 + 12 =26

C31 = 0 x (-1) + 2 x 0 + 1 x 2 = 2

C32 = 0 x 1 + 2 x 1 + 1 x 2 = 4

C33 = 0 x 5 + 2 x 3 +1 x 4 = 0 + 6 + 4 = 10

C = 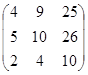C = A x B C + A x B = + =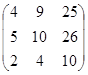

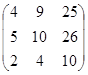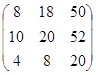
BT = 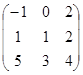= С + АВ – ВТ = - =


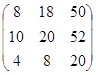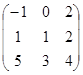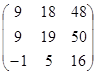
Задание 2

Вычислить определитель методом понижения порядка и приведением к треугольному виду

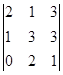
1.Метод понижения порядка

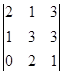= 2 x - 1 x + 3 x = 2 x (3 – 6 ) – 1 + 6 = -1

2. Приведение к треугольному виду

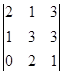
вторую строку умножаем на 2 и с второй строки вычитаем первую

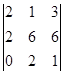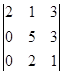== 5 x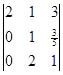

вторую строку умножаем на 2 и вычитаем из 3


(5) 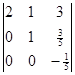= 5 x 1 x= -1

Задание 3

Решить систему уравнений методами Крамера, Гаусса, матричным способом

1.84x1 + 2.25x2 + 2.53x3 = - 6.09

2.32x1 + 2.60x2 + 2.82x3 = - 6.98

Задание 4

Даны комплексные числа z1 и z2 . Найти модули и аргументы чисел, изобразить числа на плоскости, представить в тригонометрической и показательной формах, найти

z1 + z2 , z1 - z2 , z1 *z2 , z1 :z2 , .

1.Модуль- r,- аргумент.

Z1 = 2 +3 j r = = = =3,606

= arctg=0,983 или 62,58

Z2 = 4 – 2j r = = = = 4,472

= arctg)= - 0,464 или –29,517

Z1 =r1 (cos1 +jsin1 )= x (cos(0,983) + jsin(0,983))

Z2 =r2 (cos2 +jsin2 )= x (cos(-0,464) + jsin(-0,464))

Z1 +Z2 = 2 + 3j + 4 – 2j = 6 + j

Z1 -Z2 =( 2 + 3j) – (4 – 2j) = 2 + 3j – 4 + 2j =-2 + 5j

Z1 x Z2 = (2 + 3j) x (4 – 2j) = 8 - 4j + 12j – 6j2 = 8 + 8j+ 6= 14 + 8j

= = ==

===0,1 +0,8j

(a+b)3 = a3 + 3a2 b+3ab2 + b3

Z1 =(2 + 3j)3 = 23 + 3 x 22 x 3j + 3 x 2 x (3j)2 +(33 x j2 x j) = 8 +36j – 54 – 27j

= -46 + 9j

Похожие работы

  • Системы линейных уравнений и неравенств

    Основные понятия теории систем уравнений. Метод Гаусса — метод последовательного исключения переменных. Формулы Крамера. Решение систем линейных уравнений методом обратной матрицы. Теорема Кронекер–Капелли. Совместность систем однородных уравнений.

  • Математика матрица

    Матрицы Матрица - прямоугольная (в частном случае квадратная) таблица с числами. Матрица m × n - это таблица из m строк и n столбцов. Если m = n, матрицу называют квадратной матрицей порядка n.

  • Алгебра матриц. Системы линейных уравнений

    Выполнение действий над матрицами. Определение обратной матрицы. Решение матричных уравнений и системы уравнений матричным способом, используя алгебраические дополнения. Исследование и решение системы линейных уравнений методом Крамера и Гаусса.

  • Метод Крамера

    Министерство рыбного хозяйства Владивостокский морской колледж ТЕМА: “ Системы 2-х , 3-х линейных уравнений. Правило Крамера. ” г. Владивосток

  • Матрицы Метод Гаусса

    КОСТРОМСКОЙ ФИЛИАЛ ВОЕННОГО УНИВЕРСИТЕТА РХБ ЗАЩИТЫ Кафедра «Автоматизации управления войсками» Только для преподавателей "Утверждаю"

  • Матрицы действия с ними

    Контрольная работа на тему: «Матрицы, действия с ними» Историческая справка Понятие Матрица (в математике) было введено в работах У. Гамильтона и А. Кэли в середине 19 века. Основы теории созданы К. Вейерштрассом и Ф. Фробениусом (2-я половина 19 века и начало 20 века). И.А. Лаппо-Данилевский разработал теорию аналитических функций от многих матричных аргументов и применил эту теорию к исследованию систем дифференциальных уравнений с аналитическими коэффициентами.

  • Матричная форма формулы Крамера

    С.К. Соболев Матричный способ решения СЛАУ, формулы Крамера, свойство присоединенной матрицы и основное свойство линейной зависимости. Рассмотрим

  • Основы высшей матиматики

    Вычисление определителя 4-го порядка, математическое решение системы методами матрицы, Крамера и Гаусса. Характеристика понятий невырожденной и обратной, транспонированной и присоединенной матрицы, нахождение алгебраических дополнений элементов таблицы.

  • Определители матрицы и системы линейных алгебраических уравнений

    Основные действия над матрицами, операция их умножения. Элементарные преобразования матрицы, матричный метод решения систем линейных уравнений. Элементарные преобразования систем, методы решения произвольных систем линейных уравнений, свойства матриц.

  • Системы линейных уравнений

    Критерий совместности. Метод Гаусса. Формулы Крамера. Матричный метод.