Название: Решение дифференциальных уравнений 2
Вид работы: контрольная работа
Рубрика: Математика
Размер файла: 384.72 Kb
Скачать файл: referat.me-215398.docx
Краткое описание работы: Контрольная работа Вычислить предел функции. Вычислить производную функции. Исследовать функции f(х) и g(х) и построить графики. Вычислить неопределенные интегралы.
Решение дифференциальных уравнений 2
Контрольная работа
1. Вычислить предел функции.
2. Вычислить производную функции.
3. Исследовать функции f(х) и g(х) и построить графики.
4. Вычислить неопределенные интегралы.
5. Вычислить площадь фигуры, ограниченной графиками функций f(х) и g(х).
6. Найти общее решение дифференциального уравнения и построить графики двух различных частных решений этого уравнения.
7. Найти частное решение дифференциального уравнения, удовлетворяющее указанному условию.
8. Найти частное решение дифференциального уравнения, удовлетворяющее указанным условиям.
9. Исследовать ряд на сходимость.
10. Найти радиус и интервал сходимости степенного ряда.
Вариант 0
1. а) 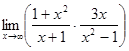 ; б)
; б) 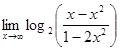 ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) 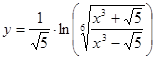 ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = x-1, g(x) = x2 -4x + 3.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 1
1. а) 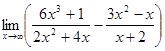 ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) 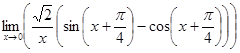 ; е)
; е) ![]() .
.
2. а) y = ln(tg x); б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = (x+2)/2, g(x) =(- x2 +7x + 2)/2.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 2
1. а) 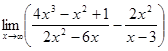 ; б)
; б) ![]() ;
;
в) 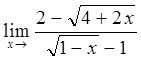 ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) 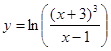 ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = x-3, g(x) = x2 +4x -3.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 3
1. а) 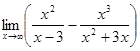 ; б)
; б) 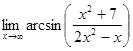 ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) =1- x, g(x) = 3 - 2x - x2.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 4
1. а) 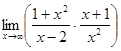 ; б)
; б) 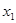 ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = x, g(x) = 2 + 2x - x2 .
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 5
1. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) 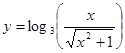 ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = x2 - x + 1, g(x) = x + 1.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 6
1. а) 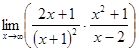 ; б)
; б) 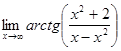 ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б)![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = 2 - 2x2, g(x) = x+1.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 7
1. а) 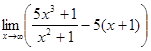 ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = x2 + 3x + 1, g(x) = -2x - 3.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 8
1. а) 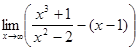 ; б)
; б) 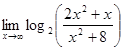 ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = -3x2 +21x - 11, g(x) = 3x + 4.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 9
1. а) 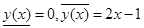 ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = 2x - 3, g(x) = -x2 + 3x - 1.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Похожие работы
-
Контрольная работа по Математике 3
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНСТИТУТДИСТАНЦИОННОГО ОБРАЗОВАНИЯ Кафедра «Бухгалтерский учет, анализ и аудит»
-
Математические последовательности Предел функции
Задание 1 Вычислите последовательности Решение. Рассмотрим последовательность для любого натурального Следовательно, множество является ограниченным сверху. Это означает, что последовательность
-
Контрольная работа
385. Вычислить несобственные интегралы или установить их расходимость. По определению несобственного интеграла имеем: Интеграл сходится. 301. Найти неопределенный интеграл.
-
по линейной алгебре
Министерство образования РФ Московский государственный университет сервиса Региональный институт сервиса Контрольная работа по математике Выполнил студент 1 курса
-
Контрольная работа по Высшей математике
федеральное агентство по образованию ростовский институт (филиал) государственного образовательного учреждения высшего профессионального образования
-
Дифференцирование. Интегрирование
Методика и основные этапы нахождения производной функции. Исследование методами дифференциального исчисления и построение графика функции. Порядок определения экстремумов функции. Вычисление неопределенных и определенных интегралов заменой переменной.
-
Интегралы, объем тела вращения, метод наименьших квадратов
Неопределенный интеграл. Объем тела вращения. Эмпирическая формула. Сходимость ряда. Вычисление объема тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями. Исследование на условную сходимость по признаку Лейбница.
-
Дифференциальные уравнения
Вычисление первого и второго замечательных пределов, неопределенного и определенного интегралов, площади криволинейной трапеции, координат середин сторон треугольника с заданными вершинами. Определение критических точек и асимптот графика функции.
-
Высшая математика 4
Контрольная работа высшая математика ЗАДАЧА 1. Вычислить пределы функций а) —д): а) 1. ► ► ► =-∞. Решение. Предел вычислен подстановкой
-
Техника интегрирования и приложения определенного интеграла
Способы определения точного значения интеграла по формуле Ньютона-Лейбница и приближенного значения интеграла по формуле трапеций. Порядок нахождения координаты центра тяжести однородной плоской фигуры ограниченной кривой, особенности интегрирования.