Название: Основные понятия математического анализа

Вид работы: изложение

Рубрика: Математика

Размер файла: 111.77 Kb

Скачать файл: referat.me-215810.docx

Краткое описание работы: Определение определенного интеграла, правила вычисления площадей поверхностей и объемов тел с помощью двойных и тройных интегралов. Понятие и виды дифференциальных уравнений, способы их решения. Действия над комплексными числами, понятие и свойства рядов.

Основные понятия математического анализа

Содержание

Двойные интегралы

Определение определенного интеграла

Правило вычисления двойного интеграла.

Вычисление объемов тел с помощью двойного интеграла

Вычисление площадей поверхностей фигур с помощью двойного интеграла.

Тройные интегралы

Вычисление объемов тел с помощью тройного интеграла.

Несобственные интегралы.

Дифференциальные уравнения.

1. Дифференциальные уравнения первого порядка с разделяющимися переменными

2. Однородные дифференциальные уравнения первого порядка

3. Линейные дифференциальные уравнения

4. Уравнения Бернулли

Дифференциальные уравнения второго порядка.

Три случая понижения порядка.

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Комплексные числа

Геометрическое изображение комплексных чисел

Действия над комплексными числами.

Произведение.

Частное.

Возведение в степень.

Извлечение корня

Ряды.

Числовые ряды.

Свойства числовых рядов.

Знакоположительные ряды

Признаки сходимости и расходимости знакоположительных рядов.

Знакопеременные и знакочередующиеся ряды.

ДВОЙНЫЕ ИНТЕГРАЛЫ

Определение определенного интеграла

- интегральная сумма.

Геометрический смысл ОИ : равен площади криволинейной трапеции.

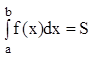
Аналогично ОИ выводится и двойной интеграл.

Пусть задана функция двух переменных z=f(x,y), которая определена в замкнутой области S плоскости ХОУ.

Интегральной суммой для этой функции называется сумма

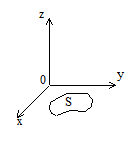
Она распространяется на те значения i и к, для которых точки (x_i ,y_k ) принадлежат области S.

Двойной интеграл от функции z=f(x,y), определенной в замкнутой области S плоскости ХОУ, называется предел соответствующей интегральной суммы.

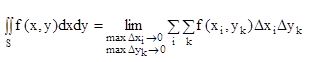
Правило вычисления двойного интеграла

Двойной интеграл вычисляется через повторные или двукратные интегралы. Различаются два основных вида областей интегрирования.

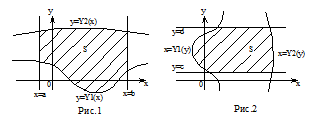
1. (Рис.1) Область интегрирования S ограничена прямыми х=а, х=в и кривыми

.

Для такой области двойной интеграл вычисляется через повторный по формуле:

Сначала вычисляется внутренний интеграл:

При вычислении внутреннего интеграла ‘у’ считается переменной, а ‘х’-постоянной.

2. (Рис.2) Область интегрирования S ограничена прямыми у=С, у=dи кривыми

.

Для такой области двойной интеграл вычисляется через повторный по формуле:

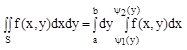
Сначала вычисляется внутренний интеграл, затем внешний.

При вычислении внутреннего интеграла ‘х’ считается переменной, а ‘у’-постоянной.

3. Если область интегрирования не относится ни к 1 ни ко второму случаю, то разбиваем ее на части таким образом, чтобы каждая из частей относилась к одному из этих двух видов.

Вычисление объемов тел с помощью двойного интеграла

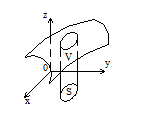
Объем тела, ограниченного сверху поверхностью z=f(x,y), снизу- плоскостью z=0 (плоскость ХОУ) и с боков- цилиндрической поверхностью, вырезающей на плоскости ХОУ область S, вычисляется по формуле:

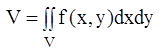
Вычисление площадей поверхностей фигур с помощью двойного интеграла

Если гладкая поверхность задана уравнением z=f(x,y), то площадь поверхности (Sпов.), имеющей своей проекцией на плоскость ХОУ область S, находится по формуле:

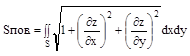- площадь поверхности.

ТРОЙНЫЕ ИНТЕГРАЛЫ

Определяется аналогично двойному интегралу.

Тройной интеграл от функции U=f(x,y,z), распространенным на область V, называется предел соответствующей трехкратной суммы.

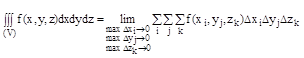
Вычисление тройного интеграла сводится к последовательному вычислению обыкновенных (однократных) нтегралов.

Вычисление объемов тел с помощью тройного интеграла

Объем тела вычисляется по формуле:

НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

Это интегралы: - с бесконечными пределами; - от неограниченной функции.

Первый вид

Несобственные интегралы с бесконечными пределами имеют вид:

; ;

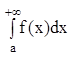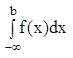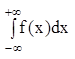
Несобственные интегралы от функции в пределах от (а) до () определяются равенством.

1 .; 2 . ; 3 .

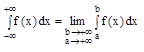
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся ; если предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся (ряд сходится или расходится?). Это и есть ответ.

Второй вид

Несобственные интегралы от неограниченной функции имеют вид: , где существует точка “с” (точка разрыва) такая, что ; , т.е. (в частности c=a; c=b).

Если функция f(x) имеет бесконечный разрыв в точке “с” отрезка [a;b] и непрерывна при или , то полагаем:

Если пределы в правой части последнего равенства существуют и конечны, то несобственный интеграл сходится , если пределы не существуют или равны бесконечности - то расходятся .

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

1 . Дифференциальное уравнение - уравнение , связывающее независимую переменную х, искомую функцию f(x) и ее производные .

Символически дифференциальное уравнение выглядит:

F(x,y,y’,y’’…,y^{( n )} )=0 или .

2 . Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение:

Пример.

F(x,y,y’)=0- дифференциальное уравнение первого порядка.

F(x,y,y’,y’’)=0- дифференциальное уравнение второго порядка.

3 . Решением дифференциального уравнения называется всякая функция , которая при подстановке в уравнение, обращает его в верное тождество.

Для того чтобы решить дифференциальное уравнение надо его проинтегрировать.

Пример .

Дифференциальное уравнение первого порядка.

Общее и частное решения.

F(x,y,y’)=0

Это уравнение можно привести к виду y’=f(x,y).

Интегрируем уравнение.

После вычисления возникает постоянная С. Поэтому решение фактически зависит не только от х, но и от С, т.е. y=f(x,C). Придавая С различные значения, мы получаем множество различных решений дифференциального уравнения. Эти решения (y=f(x,C)) называются общим решением дифференциального уравнения.

Придавая С различные значения получаем различные решения дифференциального уравнения. Так как С имеет бесконечное множество значений, то и решений будет бесконечное множество (которые отличаются друг от друга путем сдвига на несколько единиц).

Геометрически общее решение представляет собой семейство кривых на координатной плоскости ХОУ.

Частное решение .

Пусть в дифференциальном уравнении заданы дополнительные условия, что при х=х0 функция принимает значение у=у0. Это дополнительное условие называется начальным условием и записывается: а ). у=у0 при х=х0; б ). ; в ). у(х0)=у0.

Геометрически начальное условие означает некоторую точку (х0,у0) на плоскости ХОУ.

Подставляя в начальное условие , находим вполне определенные значения постоянной С. Тогда является частным решением уравнения.

Геометрически частное решение обозначает: начальное условие задает некоторую точку на плоскости и из семейства кривых (общее решение) выбирается та единственная кривая, которая проходит через эту точку.

Теорема существования и единственности решения дифференциального уравнения (теорема Коши ).

Если в дифференциальном уравнении y=f(x,y) функция f(x,y) и ее частная производная определены и непрерывны в некоторой области Д на плоскости ХОУ, то какова бы ни была внутренняя точка (х0,у0) этой области, данное уравнение имеет единственное решение , удовлетворяющее начальному условию у=у0 при х=х0.

Геометрически смысл заключается в следующем: каждой точке (х0,у0) области Д соответствует только одна интегральная кривая, проходящая через эту точку (каждой точке соответствует только одно частное решение).

Замечание . “Найти частное решение”=“Решить задачу Коши”.

Существует 4 вида дифференциальных уравнений первого порядка.

1. Дифференциальные уравнения первого порядка с разделяющимися переменными.

Дифференциальные уравнения первого порядка в общем виде можно записать либо через производные F(x,y,y’)=0, либо через дифференциалы

.

Дифференциальное уравнение- уравнение с разделяющимися переменными, если его можно представить в виде:

- - через производную.

- - через дифференциал.

В этих уравнениях в произведениях стоят функции, каждая из которых зависит от одной переменной (х или у). Т.е. уравнение будет уравнением с разделяющимися переменными, если его можно преобразовать так, чтобы в одной его части была только одна переменная, а в другой – только другая.

Замечание. При решении дифференциальное уравнение ответу можно придать различную форму в зависимости от того, как записана произвольная постоянная С.

Решение.

-

; -интегрируем и получаем решение.

-

;

Однородные дифференциальные уравнения первого порядка

Функция f(x,y) называется однородной функцией n–го измерения, если при любом выполняется условие: .

Дифференциальное уравнение y’=f(x,y) есть однородное, если функция f(x,y) является однородной функцией нулевого измерения.

Дифференциальное уравнение P(x,y)dx+Q(x,y)dy=0 однородное, если P(x,y) и Q(x,y) являются однородными функциями одного и того же измерения.

P(x,y)dx=-Q(x,y)dy;

Однородное уравнение всегда можно привести к виду и с помощью замены однородное уравнение всегда приводится к уравнению с разделяющимися переменными (; y=xt; y’=t+xt’).

Линейные дифференциальные уравнения

ЛДУ - уравнения вида y’+P(x)y=Q(x)– первого порядка относительно у и у’.

Для решения ЛДУ применяем замену: y=UV, тогда y’=U’V+UV’

U’V+UV’+P(x)UV=Q(x)

V(U’+P(x)U)+UV’=Q(x)

Далее U’+P(x)U=0, получаем два уровнения с разделяющимися переменными:

1 ). U’+P(x)U=0 находим U. 2 ). UV’=Q(x) находим V. . С ставится только при вычислении второго уравнения.

Замечание . Выражение, стоящее в скобках, можно прировнять к нулю, т.к. одну из функций можно взять произвольной, другую – определяем на основании ЛДУ.

Уравнения Бернулли

УБ - дифференциальные уравнения вида y’+P(x)y=Q(x)*yⁿ , где

- т.к. при этих значениях уравнение будет линейным.

УБ решаются так же, как и линейные.

Дифференциальные уравнения второго порядка

Дифференциальные уравнения второго порядка в общем виде записываются: F(x,y,y’,y’’)=0

Как и в случае дифференциальных уравнений первого порядка для решения дифференциальных уравнений второго порядка существуют общее и частное решения. Но, если для дифференциальных уравнений первого порядка решение зависело от одной константы С, то для дифференциальных уравнений второго порядка решение зависит от двух постоянных: - общее решение.

Если заданы начальные условия (у=у0, у=у0 при х=х0), то получаем частное решение, удовлетворяющее этим начальным условиям.

Начальные условия так же могут задаваться в виде:

у=у0 при х=х0; у=у1 при х=х1.

Три случая понижения порядка

1. Случай непосредственного интегрирования

F(x,y”)=0

y’’=f(x)- решение этого уравнения находится путем двукратного интегрирования.

; ; ;

2. Когда дифференциальное уравнение явно не содержит у, т.е. F ( x , y ’, y ”)=0

С помощью замены у’=р; это уравнение приводим к уравнению первого порядка .

3. Когда дифференциальное уравнение явно не содержит х, т.е. F ( y , y ’, y ”)=0.

С помощью замены y’=p, это уравнение приводим к уравнению первого порядка .

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Линейными однородными дифурами второго порядка с постоянными коэффициентами называются уравнения вида:

y’’+py’+qy=0,

где p и q – некоторые числа.

Составим характеристическое уравнение:

,

которое получается из данного уравнения путем замены в нем производных искомой функции соответствующими степенями “к”. Причем сама функция заменяется единицей.

Если к1 и к2 – корни характериситического уравнения, то общее решение однородного уравнения имеет один из следующих трех видов:

1). , если к1 и к2 – действительные и различные, т.е. D>0.

2). , если к1 и к2 – действительные и равные, т.е. к1=к2, D=0.

3). , если к1 и к2 – комплексные, т.е. ; D<0.

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Имеют вид:

,

где p и q– некоторые числа.

Общее решение имеет вид:, где

y0 - общее решение соответствующего однородного уравнения; - частное решение соответствующего однородного уравнения.

Т.е. для нахождения общего решения неоднородного уравнения ‘у’, сначала находят общее решение соответствующего однородного уравнения у0, а затем частное решение , и складывают их.

Частное решение неоднородного уравнения находится методом неопределенных коэффициентов .

Для нахождения частных решений рассмотрим несколько случаев.

1. Пусть правая часть f(x) имеет вид:

, где P_n (x) – многочлен n–ой степени.

Тогда возможны следующие 3 случая:

А) . Если ‘а’ не является корнем характеристического уравнения k² +pk+q=0, то частное решение имеет вид: , где Q_n (x) – многочлен той же степени, что и P_n (x), только с неопределенными коэффициентами.

Например .

P_n (x)=8 - многочлен 0-ой степени (n=0). Q_n (x)=A;

P_n (x)=2x-3 - многочлен 1-ой степени (n=1). Q_n (x)=Ax+B;

P_n (x)=x² - многочлен 2-ой степени (n=2). Q_n (x)=Ax² +Bx+C;

P_n (x)=3x³ -3x - многочлен 3-ей степени (n=3). Q_n (x)=Ax³ +Bx² +Cx+D.

Замечание . Многочлен Q_n (x) всегда должен быть полный, т.е. содержать все степени х. Коэффициенты А,В,С,Д и т.д. находим по методу неопределенных коэффициентов непосредственно при решении каждого конкретного уравнения.

Б). Если а является однократным корнем характеристического уравнения k² +pk+q=0, то есть совпадает с одним из корней характеристического уравнения, то частное решение имеет вид: .

В). Если а является двукратным корнем характеристического уравнения k² +pk+q=0, то есть совпадает с двумя корнями характеристического уравнения, то частное решение имеет вид: .

Итог .

Если , то , где r– кратность корня ‘а’ в характеристическом уравнении, т.е. r=0, если ‘а’ не есть корень; r=1, если ‘а’ совпадает с одним из корней; r=2, если ‘а’ совпадает с двумя корнями.

2. Если правая часть f(x) имеет вид:, где P_n ( x ) –многочлен n–ой степени; Q_m ( x ) -многочлен m–ой степени.

Тогда возможны следующие два случая:

А). Если не является корнем характеристического уравнения k² +pk+q=0 (), то частное решение имеет вид: , где S_N (x), T_N (x)–многочлены степени N с неопределенными коэффициентами, где N=max из n и m (N=max{n,m}), т.е. степень N многочленов S_N (x) и T_N (x) равна наибольшей из степеней многочленов P_n (x) и Q_m (x).

Б). Если является корнем характеристического уравнения k² +pk+q=0 (), то частное решение имеет вид:

Замечание .

- Если в правой части f(x) неоднородного уравнения во 2 случае отсутствует одно из слагаемых, т.е. P_n (x)=0 или Q_m (x)=0, то частное решение все равно записывается в полоном виде.

- Если правая часть f(x) неоднородного уравнения в 1 и 2 случаях есть сумма нескольких функций (f(x)= f₁ (x)+ f₂ (x)+… f_n (x)), то .

- Так же рассматриваем все комбинации при расчете : cosx, sinx, xcosx, xsinx,x² cosx, x² sinx.

КОМПЛЕКСНЫЕ ЧИСЛА

Комплексным числом (z) называется выражение z=x+iy, где х и у- действительные числа, i-мнимая единица.

i определяется: i² =-1 , отсюда .

х- действительная часть (x=Rez);

у- мнимая часть (y=Imz).

Геометрическое изображение комплексных чисел

Существуют следующие формы комплексных чисел: алгебраическая (x+iy), тригонометрическая (r(cos+isin)), показательная (reⁱ ).

Всякое комплексное число z=x+iy можно изобразить на плоскости ХОУ в виде точки А(х,у).

Плоскость, на которой изображаются комплексные числа, называется плоскостью комплексного переменного z (на плоскости ставим символ z).

Ось ОХ – действительная ось, т.е. на ней лежат действительные числа. ОУ – мнимая ось с мнимыми числами.

x + iy - алгебраическая форма записи комплексного числа.

Выведем тригонометрическую форму записи комплексного числа.

;

Подставляем полученные значения в начальную форму:

, т.е.

r ( cos + isin ) - тригонометрическая форма записи комплексного числа.

Показательная форма записи комплексного числа следует из формулы Эйлера:

, тогда

z=reⁱ - показательная форма записи комплексного числа.

Действия над комплексными числами

1. сложение. z₁ +z₂ =(x1+iy1)+ (x2+iy2)=(x1+x2)+i(y1+y2);

2 . вычитание. z₁ -z₂ =(x1+iy1)- (x2+iy2)=(x1-x2)+i(y1-y2);

3. умножение. z₁ z₂ =(x1+iy1)*(x2+iy2)=x1x2+i(x1y2+x2y1+iy1y2)=(x1x2-y1y2 )+i(x1y2+x2y1);

4 . деление. z₁ /z₂ =(x1+iy1)/(x2+iy2)=[(x1+iy1)*(x2-iy2)]/[ (x2+iy2)*(x2-iy2)]=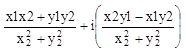

Два комплексных числа, которые отличаются только знаком мнимой единицы, т.е. z=x+iy (z=x-iy), называются сопряженными.

Произведение

- Если комплексные числа заданы в тригонометрической форме.

z1=r(cos+isin); z2=r(cos+isin).

То произведение z1*z2 комплексных чисел находится: , т.е. модуль произведения равен произведению модулей, а аргумент произведения равен сумме аргументов сомножителей.

- Если комплексные числа заданы в показательной форме.

; ;

Частное

- Если комплексные числа заданы в тригонометрической форме.

- Если комплексные числа заданы в показательной форме.

Возведение в степень

1. Комплексное число задано в алгебраической форме.

z=x+iy, то zⁿ находим по формуле бинома Ньютона :

zⁿ =(x+iy)ⁿ .

- число сочетаний из n элементов по m (число способов, сколькими можно взять n элементов из m).

; n!=1*2*…*n; 0!=1; .

Применяем для комплексного числа.

В полученном выражении нужно заменить степени i их значениями:

i⁰ =1 Отсюда, в общем случае получаем: i^{4 k} =1

i¹ =i i^4k+1 =i

i² =-1 i^4k+2 =-1

i³ =-i i^4k+3 =-i

i⁴ =1

i⁵ =i

i⁶ =-1

Пример .

i³¹ = i²⁸ i³ =-i

i¹⁰⁶³ = i¹⁰⁶² i=i

2. Если комплексное число задано в тригонометрической форме.

z=r(cos+isin), то

- формула Муавра .

Здесь nможет быть как “+” так и “-” (целым).

3. Если комплексное число задано в показательной форме:

Извлечение корня

Рассмотрим уравнение: .

Его решением будет корень n–ой степени из комплексного числа z: .

Корень n–ой степени из комплексного числа z имеет ровно n решений (значений). Корень из действующего числа n-ой степени имеет только одно решение. В комплексных – n решений.

Если комплексное число задано в тригонометрической форме:

z=r(cos+isin), то корень n-ой степени от z находится по формуле:

, где к=0,1…n-1.

РЯДЫ

Числовые ряды

Пусть переменная а принимает последовательно значения а₁ ,а₂ ,а₃ ,…,а_n . Такое перенумерованное множество чисел называется последовательностью. Она бесконечна.

Числовым рядом называется выражение а₁ +а₂ +а₃ +…+а_n +…= . Числа а₁ ,а₂ ,а₃ ,…,а_n – члены ряда.

Например.

а₁ – первый член ряда.

а_n – n-ый или общий член ряда.

Ряд считается заданным, если известен n-ый (общий член ряда).

Числовой ряд имеет бесконечное число членов.

Числители – арифметическая прогрессия (1,3,5,7…).

n-ый член находится по формуле

а_n =а₁ +d(n-1); d=а_n -а_n-1 .

Знаменатель – геометрическая прогрессия .

b_n =b₁ q^{n -1} ; .

Рассмотрим сумму первых n членов ряда и обозначим ее Sn.

Sn=а1+а2+…+а_n .

Sn – n-ая частичная сумма ряда.

Рассмотрим предел:

S - сумма ряда.

Ряда сходящийся , если этот предел конечен (конечный предел S существует).

Ряд расходящийся , если этот предел бесконечен.

В дальнейшем наша задача заключается в следующем: установить какой ряд.

Одним из простейших, но часто встречающихся рядов является геометрическая прогрессия.

, C=const.

Геометрическая прогрессия является сходящимся рядом , если , и расходящимся, если .

Также встречается гармонический ряд (ряд ). Этот ряд расходящийся .

Свойства числовых рядов

1. Если сходится а₁ +а₂ +а₃ +…+а_n +…=, то сходится и ряд а_{m +1} +а_m+2 +а_m+3 +…, полученный из данного ряда отбрасыванием первых m членов. Этот полученный ряд называется m-ым остатком ряда. И, наоборот: из сходимости m-го остатка ряда вытекает сходимость данного ряда. Т.е. сходимость и расходимость ряда не нарушается, если прибавить или отбросить конечное число его членов.

2 . Если ряд а₁ +а₂ +а₃ +… сходится и его сумма равна S, то ряд Са₁ +Са₂ +…, где С= так же сходится и его сумма равна СS.

3. Если ряды а₁ +а₂ +… и b₁ +b₂ +… сходятся и их суммы равны соответственно S1 и S2, то ряды (а₁ +b₁ )+(а₂ +b₂ )+(а₃ +b₃ )+… и (а₁ -b₁ )+(а₂ -b₂ )+(а₃ -b₃ )+… также сходятся. Их суммы соответственно равны S1+S2 и S1-S2.

4. а). Если ряд сходится, то его n-ый член стремится к 0 при неограниченном возрастании n (обратное утверждение неверно).

- необходимый признак (условие) сходимости ряда .

б). Если то ряд расходящийся – достаточное условие расходимости ряда .

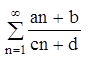-ряды такого вида исследуются только по 4 свойству. Это расходящиеся ряды.

Знакоположительные ряды

Признаки сходимости и расходимости знакоположительных рядов.

Знакоположительные ряды это ряды, все члены которых положительные. Эти признаки сходимости и расходимости мы будем рассматривать для знакоположительных рядов.

1. Первый признак сравнения.

Пусть даны два знакоположительных ряда а₁ +а₂ +а₃ +…+а_n +…=(1) и b₁ +b₂ +b₃ +…+b_n +…=(2).

Если члены ряда (1) не больше соответствующих членов ряда (2), т.е. а_n b_n и ряд (2) сходится , то и ряд (1) также сходится.

Если члены ряда (1) не меньше соответствующих членов ряда (2), т.е. а_n b_n и ряд (2) расходится , то и ряд (1) также расходится.

Этот признак сравнения справедлив, если неравенство выполняется не для всех n, а лишь начиная с некоторого.

2. Второй признак сравнения

Если существует конечный и отличный от нуля предел , то оба ряда сходятся или расходятся одновременно.

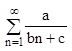-ряды такого вида расходятся по второму признаку сравнения. Их надо сравнивать с гармоническим рядом.

3. Признак Даламбера

Если для знакоположительного ряда (а₁ +а₂ +а₃ +…+а_n +…=) существует (1), то ряд сходится, если q<1, расходится, если q>1. Если q=1 то вопрос остается открытым.

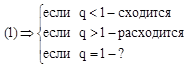
4. Признак Коши радикальный

Если для знакоположительного ряда существует предел (2), то ряд сходится, если q<1, расходится, если q>1. Если q=1 то вопрос остается открытым.

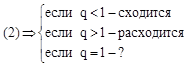
5. Признак Коши интегральный

Вспомним несобственные интегралы.

Если существует предел . Это есть несобственный интеграл и обозначается .

Если этот предел конечен, то говорят, что несобственный интеграл сходится. Ряд, соответственно, сходится или расходится.

Пусть ряд а₁ +а₂ +а₃ +…+а_n +…=- знакоположительный ряд.

Обозначим a_n =f(x) и рассмотрим функцию f(x). Если f(x)- функция положительная, монотонно убывающая и непрерывная, то, если несобственный интеграл сходится, то и данный ряд сходится. И наоборот: если несобственный интеграл расходится, то и ряд расходится.

Если ряд конечен, то он сходится.

Очень часто встречаются ряды 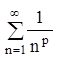- ряд Дерихле . Он сходится, если p>1, расходится p<1. Гармонический ряд является рядом Дерихле при р=1. Сходимость и расходимость данного ряда легко доказать с помощью интегрального признака Коши.

Знакопеременные и знакочередующиеся ряды

Знакопеременный ряд – это ряд, среди членов которого имеются как + так и – члены.

Частным случаем знакопеременного ряда является знакочередующийся ряд. Это ряд, у которого за каждым + членом следует -, и наоборот, т.е. знаки чередуются.

Пусть задан знакопеременный ряд а₁ +а₂ +а₃ +…+а_n +…= (1) (члены как + так и -).

Возьмем ряд (3), составленный из абсолютных величин членов ряда (1). Ряд (3) является знакоположительным рядом.

Если ряд (3) сходится, то ряд (1) также сходится и называется абсолютно сходящимся (ответ получен сразу).

Если ряд (3) расходится, а:

- ряд (1) сходится, то ряд (1) называется условно сходящимся;

- ряд (1) расходится, то ряд (1) называется расходящимся.

При исследовании знакоположительных рядов можем получить 2 ответа: ряд сходится или ряд расходится.

При исследовании знакопеременных рядов могут получиться 3 ответа: ряд сходится абсолютно, ряд сходится условно, ряд расходится.

Схема

Если (3) – сходится (1) - сходится абсолютно.

Если (3) – расходится

При исследовании на сходимость знакопеременного ряда (1) начинать надо с разбора знакоположительного ряда (3). Т.к. ряд (3)- знакоположительный ряд, то к нему можно применить все признаки сходимости для знакоположительных рядов.

Из расходимости ряда (3) не следует расходимость ряда (1), но если (3) расходится по признакам Даламбера или Коши радикальный , то расходится не только ряд (3), но и ряд (1) .

Если ряд – знакочередующийся, то для него дается еще один признак сходимости :

Признак Лейбница

Если для знакочередующегося ряда b1-b2+b3-b4+…(bn0) выполняются условия:

1 . b1b2b3b4…;

2 . , - то данный ряд сходится условно .