Название: Вычисление радиальных функций Матье-Ханкеля
Вид работы: научная работа
Рубрика: Математика
Размер файла: 205.1 Kb
Скачать файл: referat.me-216001.docx
Краткое описание работы: Условия возникновения и особенности вычисления функций Матье, характеристика дифференциального уравнения Матье. Алгоритм решения задачи и алгоритмы вычисления радиальных функций эллиптического цилиндра. Определение точности результатов вычисления.
Вычисление радиальных функций Матье-Ханкеля
Вычисление радиальных функций матье-ханкеля
Н.И. Волвенко, V курс, Институт математики и компьютерных наук ДВГУ, Т.В. Пак – научный руководитель, доцент, к.ф.-м.н., и.о. зав. кафедрой КТ
Функции Матье, в отличие от широко известных специальных функций, таких как полиномы Лежандра, функции Бесселя и Неймана, изучены ещё недостаточно полно. Почти все используемые методы расчёта связаны с разложением в ряды по более простым цилиндрическим и т.п. функциям. Недостаток таких методов в том, что они достаточно громоздки и имеют ограниченную применимость.
Функции Матье возникают при разделении переменных в уравнении Гельмгольца:
![]() , (1)
, (1)
где ![]() - некоторая вещественная положительная константа и
- некоторая вещественная положительная константа и ![]() - оператор Лапласа.
- оператор Лапласа.
Эллиптические координаты ![]() , допускающие разделение переменных связаны с декартовыми:
, допускающие разделение переменных связаны с декартовыми: ![]() ,
,![]() .
.
Полагая ![]() в методе разделения переменных, получаем уравнения:
в методе разделения переменных, получаем уравнения:
![]() ,
, ![]() ,
,
где ![]() - константа разделения. Эти уравнения являются вариантами уравнений Матье.
- константа разделения. Эти уравнения являются вариантами уравнений Матье.
Дифференциальное уравнения Матье имеет вид
![]()
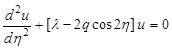 , (2)
, (2)
где обычно переменная ![]() имеет вещественное значение, а
имеет вещественное значение, а ![]() - заданный вещественный ненулевой параметр.
- заданный вещественный ненулевой параметр.
Собственные значения ![]() и граничные условия
и граничные условия
![]() (3)
(3)
соответствуют чётным функциям Матье ![]() , а собственные значения
, а собственные значения ![]() и граничные условия
и граничные условия
![]() (4)
(4)
нечётным функциям Матье
![]()
В силу свойств симметрии уравнение (2) имеет 4 типа периодических решений, называемых функциями Матье 1-ого рода: чётную π-периодическую, чётную 2π-периодическую, нечётную 2π-периодическую, нечётную π-периодическую функции, которые чаще всего обозначаются таким образом: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Собственные значения ![]() , отвечающие функциям
, отвечающие функциям ![]() ,
, ![]() ,
, ![]() ,
, ![]() , обозначаются через
, обозначаются через ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Модифицированное уравнение Матье
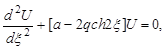 (5)
(5)
получается из уравнения Матье (2) подстановкой ![]() . В зависимости от того, будет в (5)
. В зависимости от того, будет в (5) ![]() или
или ![]() , это уравнение имеет либо решение
, это уравнение имеет либо решение ![]() , либо решение
, либо решение ![]() , которые являются соответственно чётной и нечётной функциями от ξ.
, которые являются соответственно чётной и нечётной функциями от ξ.
Функции, являющиеся решениями уравнения (5), называются радиальными функциями Матье (РФМ).
Различают РФМ 1, 2, 3 и 4 рода: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Вычисление функций Матье I рода
Радиальные функции Матье первого рода являются решениями ОДУ второго порядка
![]() ,
, ![]() (6)
(6)
удовлетворяющие в нуле условию
![]() , если
, если ![]() (7)
(7)
![]() , если
, если ![]()
И на бесконечности условию
![]() ~
~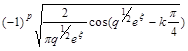 ,
, ![]() (8)
(8)
где ![]() - задано, а
- задано, а ![]() (
(![]() ) - собственные значения задачи (2), (3), (4),
) - собственные значения задачи (2), (3), (4),
![]()
Параметр ![]() используются для различия случаев использования чётного или нечётного номера собственного значения для π и 2π периодических собственных функций:
используются для различия случаев использования чётного или нечётного номера собственного значения для π и 2π периодических собственных функций:
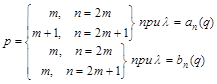
Для решения задачи (6)-(8) используем модификацию метода фазовых функций.
Введём замену переменных:
![]() (9)
(9)
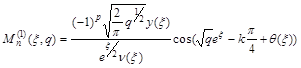 (10)
(10)
Здесь ![]() - "масштабирующая" функция, положительная на
- "масштабирующая" функция, положительная на ![]() , удовлетворяющая условию
, удовлетворяющая условию ![]() при
при ![]() , её выбор находится в нашем распоряжении.
, её выбор находится в нашем распоряжении.
Подставляя (9), (10) в исходное уравнение (6) задачи для ![]() и
и ![]() :
:
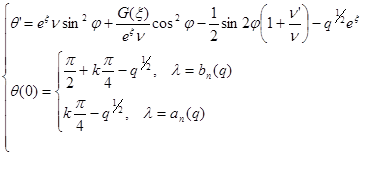 (11)
(11)
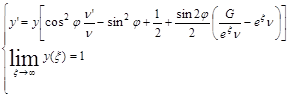 (12)
(12)
где ![]() и
и ![]() .
.
Для совместного решения задач Коши для ![]() и
и ![]() используется следующий приём. Функцию
используется следующий приём. Функцию ![]() ищем в точках
ищем в точках ![]() . На каждом из отрезков
. На каждом из отрезков ![]() вспомогательные функции
вспомогательные функции ![]() находятся, как решение задач Коши
находятся, как решение задач Коши
![]() (13)
(13)
где ![]() .
.
Поскольку для любых решений ![]() и
и ![]() , уравнений (12) и (13) справедливо соотношение
, уравнений (12) и (13) справедливо соотношение ![]() , получаем рекуррентные формулы «назад» для вычисления
, получаем рекуррентные формулы «назад» для вычисления ![]() ,
, ![]() ,
,
![]() ,
, ![]() , (14)
, (14)
причём ![]() .
.
Итак, краткий алгоритм решения задачи (6)-(8) состоит в следующем:
1. Решаются совместно задачи Коши (11), (12) запоминая в точках разбиения отрезка ![]() величины
величины ![]() ,
, ![]() ,
, ![]() ;
;
2. Полагая ![]() , по формуле (14) вычисляем
, по формуле (14) вычисляем ![]() ,
, ![]() ;
;
3. По формуле (10) вычисляем функции ![]() ,
, ![]() ;
;
4. Из (9) и (10) получаем выражение для производной функции ![]()
![]() .
.
В качестве сглаживающей функции предлагается следующая функция
![]() , где
, где 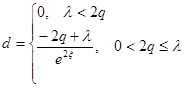 .
.
Вычисление функций Матье III рода
Волновая радиальная функция Матье-Ханкеля третьего рода является решением обыкновенного дифференциального уравнения второго ворядка на полубесконечном интервале:
![]() ,
,![]() . (15)
. (15)
Условие на бесконечности
![]() ~
~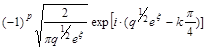 ,
, ![]() . (16)
. (16)
Для уравнения (15) условие (16) эквивалентно условию:
![]() ,
,
и при достаточно больших ![]() линейному соотношению:
линейному соотношению:
![]() ,
, ![]() .
.
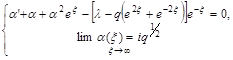 (17)
(17)
Решение задачи (17) существует, единственно и при достаточно больших ![]() представимо асимптотическим рядом
представимо асимптотическим рядом ![]() .
.
Рассмотрим алгоритм нахождения функций ![]() . Для их вычисления нужно перенести граничное условие
. Для их вычисления нужно перенести граничное условие
![]() ,
,
где 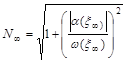 , справа налево от точки
, справа налево от точки ![]() до точки
до точки ![]() .
.
Воспользуемся вариантом ортогональной дифференциальной прогонки.
По всему отрезку ![]() переносим соотношение
переносим соотношение
![]() ,
,
потребовав выполнение условия ![]() для всех
для всех ![]() ,
, ![]() , где
, где ![]() и
и ![]() удовлетворяют системе дифференциальных уравнений 1-ого порядка
удовлетворяют системе дифференциальных уравнений 1-ого порядка
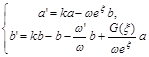 .
.
Функции Матье 3-его рода ищем по формуле:
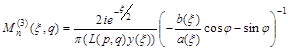 ,
,
где ![]() .
.
Функции Матье 2-ого рода вычисляются по формуле:
![]() .
.
функция матье дифференциальное уравнение
Описанные алгоритмы вычисления радиальных функций эллиптического цилиндра опробованы в широком диапазоне изменения параметров. Точность результатов определяется точностью используемого метода Рунге-Кутта для решения соответствующих задач Коши.
Литература
1. Абрамов А.А., Дышко А.Л., Пак Т.В. и др. Численные методы решения задач на собственные значения для систем обыкновенных дифференциальных уравнений с особенностями. – Третья конференция по дифференциальным уравнениям и приложениям. – Тезисы докладов. Руссе, Болгария, 1985. – с.4.
2. Миллер У. мл. Симметрия и разделение переменных / Пер. с англ. – М.: Мир, 1981. – 342 с.
3. Справочник по специальным функциям с формулами, графиками таблицами. / Под редакцией М. Абрамовица, И. Стигана. – М. – 1979. – 832 с.:ил.
Похожие работы
-
Решение смешанной задачи для уравнения гиперболического типа методом сеток
Решение смешанной задачи для уравнения гиперболического типа методом сеток Рассмотрим смешанную задачу для волнового уравнения ) (1). Задача состоит в отыскании функции
-
Решение нелинейных уравнений
Задание №1 Отделить корни уравнения графически и уточнить один из них: · методом половинного деления; · методом хорд; · методом касательных; · методом секущих;
-
Вычисление пределов функций, производных и интегралов
Изучение способов нахождения пределов функций и их производных. Правило дифференцирования сложных функций. Исследование поведения функции на концах заданных промежутков. Вычисление площади фигуры при помощи интегралов. Решение дифференциальных уравнений.
-
Вычисление определенных интегралов. Квадратурные формулы
Решение задачи по вычислению определенного интеграла с помощью квадратурных формул и основная идея их построения. Количество параметров квадратурного выражения, степень подынтегральной функции. Построение квадратурных формул с плавающими узлами.
-
Нелинейное уравнение и интервал изоляции корня
Изучение методов уточнения корней нелинейных уравнений (половинного деления, хорд, касательных, простой итерации). Метод хорд и касательных дает высокую скорость сходимости при решении уравнений, и небольшую - метод половинного деления и простой итерации.
-
Цилиндр
Цилиндр-это фигура, состоящая из двух кругов, совмещаемых параллельным переносом и всех отрезков, соединяющих соответствующие точки этих кругов.
-
Вычисление площади сложной фигуры методом имитационного моделирования
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ (ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ) Расчет площади сложной фигуры с помощью метода имитацеонного моделирования .
-
Вычисление определенного интеграла методом трапеций и средних прямоугольников
БЕЛОРУССКИЙ АГРАРНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ КУРСОВАЯ РАБОТА на тему “вычисление определенного интеграла методами трапеций и средних прямоугольников”
-
Численные методы решения обыкновенных дифференциальных уравнений
Лабораторная работа 1 Численные методы решения обыкновенных дифференциальных уравнений (4 часа) При решении многих физических и геометрических задач приходится искать неизвестную функцию по данному соотношению между неизвестной функцией, ее производными и независимыми переменными. Такое соотношение называется
-
Решения смешанной задачи для уравнения гиперболического типа методом сеток
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Р.Ф. КУРГАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра прикладной и высшей математики Лабораторная работа № 43