Название: по численным методам
Вид работы: курсовая работа
Рубрика: Математика
Размер файла: 307.47 Kb
Скачать файл: referat.me-216305.docx
Краткое описание работы: 1. Методом Крылова развернуть характеристический определитель матрицы А= . Исходную систему линейных уравнений решить методом Жордана-Гаусса. Решение. Метод Крылова основан на свойстве квадратной матрицы обращать в нуль свой характеристический многочлен.
по численным методам
1. Методом Крылова развернуть характеристический определитель матрицы А=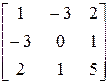 . Исходную систему линейных уравнений решить методом Жордана-Гаусса.
. Исходную систему линейных уравнений решить методом Жордана-Гаусса.
Решение. Метод Крылова основан на свойстве квадратной матрицы обращать в нуль свой характеристический многочлен.
Согласно теореме Гамильтона-Кали, всякая квадратная матрица является корнем своего характеристического многочлена и, следовательно, обращает его в нуль.
Пусть
![]() – (1)
– (1)
характеристический многочлен.
Заменяя в выражении (1) величину ![]() на
на ![]() , получим
, получим
![]() . (2)
. (2)
Возьмем произвольный ненулевой вектор
![]() . (3)
. (3)
Умножим обе части выражения (2) на ![]() :
:
![]() (4)
(4)
Положим
![]() , (5)
, (5)
т.е.
![]() (6)
(6)
Учитывая (5), выражение (4) запишем в виде
![]() , (7)
, (7)
или в виде
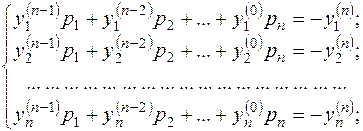
Решаем систему (7). Если эта система имеет единственное решение, то ее корни ![]() являются коэффициентами характеристического многочлена (1).
являются коэффициентами характеристического многочлена (1).
Если известны коэффициенты ![]() и корни
и корни ![]() характеристического многочлена, то метод Крылова дает возможность найти соответствующие собственные векторы по следующей формуле:
характеристического многочлена, то метод Крылова дает возможность найти соответствующие собственные векторы по следующей формуле:
![]() (8)
(8)
Здесь ![]() – векторы, использованные при нахождении коэффициентов
– векторы, использованные при нахождении коэффициентов ![]() методом Крылова, а коэффициенты
методом Крылова, а коэффициенты ![]() определяются по схеме Горнера
определяются по схеме Горнера
![]() (9)
(9)
Используя все выше сказанное, развернем характеристический определитель матрицы А=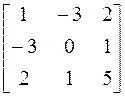 методом Крылова.
методом Крылова.
Выберем в качестве начального следующий вектор:
![]() ,
, ![]()
Вычислим
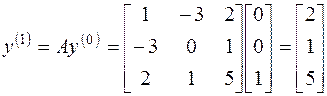
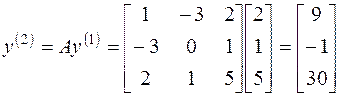
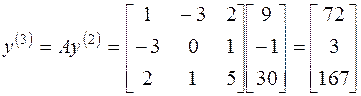
Составим матричное уравнение
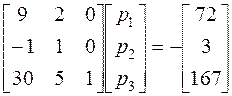 , или
, или 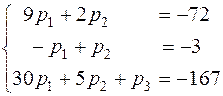
Полученную систему уравнений решим методом Жордана-Гаусса.
|
|
|
|
|
|
|
|
| 1 |
9 |
2 |
0 |
-72 |
-61 |
-61 |
| -1 |
1 |
0 |
-3 |
-3 |
-3 |
|
| 30 |
5 |
1 |
-167 |
-131 |
-131 |
|
| 2 |
1 |
2/9 |
0 |
-8 |
-61/9 |
-61/9 |
| 0 |
11/9 |
0 |
-11 |
-88/9 |
-88/9 |
|
| 0 |
-15/9 |
1 |
657/9 |
651/9 |
651/9 |
|
| 3 |
1 |
0 |
0 |
-6 |
-5 |
-5 |
| 0 |
1 |
0 |
-9 |
-8 |
-8 |
|
| 0 |
0 |
1 |
58 |
59 |
59 |
|
| 4 |
1 |
0 |
0 |
|||
| 0 |
1 |
0 |
||||
| 0 |
0 |
1 |
Исходя из результатов таблицы, имеем ![]() .
.
Таким образом характеристическое уравнение матрицы ![]() имеет вид
имеет вид
![]()
2. Для определения собственных чисел матрицы ![]() необходимо решить полученное характеристическое уравнение третьей степени
необходимо решить полученное характеристическое уравнение третьей степени
![]()
Данное кубическое уравнение невозможно решить стандартными средствами. Воспользуемся для этой цели числовыми методами, а точнее методами приближенного вычисления.
2.1 Исследование функции.
Вычислим первую и вторую производные данной функции
![]()
![]()
Необходимо выбрать интервал, на котором будем находить решение.
Для отделения корней существует несколько способов. Наиболее популярные из них – графический и аналитический.
В литературе рассматриваются эти способы по отдельности. По заданию курсовой работы требуется отделить корни каждым из этих способов. Рискну нарушить это требование, и объединить эти два способа в один. То есть исследовать функцию аналитически и по результатам исследования построить приблизительный график функции.
Областью значений исходного уравнения является вся ось ![]() .
.
Приравняв первую производную к нулю, мы можем получить критические точки данной функции (точки минимумов и максимумов, или же точки, в которых функция не определена).
![]()
![]()
![]()
Стоит отметить, что для вычисления квадратного корня, также применимы числовые методы, на которых и основаны микрокалькуляторы и программы для ЭВМ. Данные методы основаны на логарифмировании корня и последующего вычисления.
![]()
![]() вычисляется при помощи числового ряда
вычисляется при помощи числового ряда
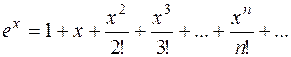
Уравнение ![]() имеет решение
имеет решение 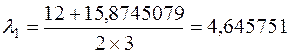 ,
, 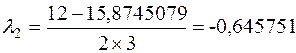 . Изменив знак равенства на знак неравенства (< или >), можем найти промежутки возрастания и убывания функции.
. Изменив знак равенства на знак неравенства (< или >), можем найти промежутки возрастания и убывания функции.
Функция возрастает на промежутке ![]() и убывает на промежутке
и убывает на промежутке ![]() . Подставив в исходное уравнение значения критических точек, имеем в результате для
. Подставив в исходное уравнение значения критических точек, имеем в результате для ![]() и для
и для ![]() .
.
Приравняв вторую производную к нулю, мы можем найти точку перегиба и, соответственно, найти интервал, на котором функция выпуклая и вогнутая.
![]()
![]()
![]()
Далее необходимо найти, интервалы, в которых график функции пересекает ось ![]() .
.
Сразу можно определиться, что так при ![]() значение функции больше нуля, а при
значение функции больше нуля, а при ![]() - меньше нуля, то одна из точек пересечения, будет лежать на данном интервале. Произведя не хитрые математические вычисления значения функции для
- меньше нуля, то одна из точек пересечения, будет лежать на данном интервале. Произведя не хитрые математические вычисления значения функции для ![]() , сузим интервал до
, сузим интервал до ![]() .
.
Далее рассмотрим оставшиеся два интервала.
Известно, что при ![]() - значение функции отрицательно, а в первой критической точке положительно, то будем сужать этот промежуток. В данном случае применим метод половинного деления.
- значение функции отрицательно, а в первой критической точке положительно, то будем сужать этот промежуток. В данном случае применим метод половинного деления.
|
|
|
| 0 |
58 |
| -100 |
-1059042 |
| -50 |
-139492 |
| -25 |
-19092 |
| -12 |
-2426 |
| -6 |
-320 |
| -3 |
4 |
| -5 |
-172 |
| -4 |
-66 |
|
|
|
| 4 |
-10 |
| 100 |
939158 |
| 50 |
109608 |
| 25 |
11708 |
| 12 |
814 |
| 6 |
4 |
| 5 |
-12 |
Таким образом получили еще один интервал ![]() .
.
Следующий будет от ![]() и до бесконечности.
и до бесконечности.
Произведем аналогичные вычисления и получим промежуток ![]()
На основании произведенного анализа построим график исходной функции.
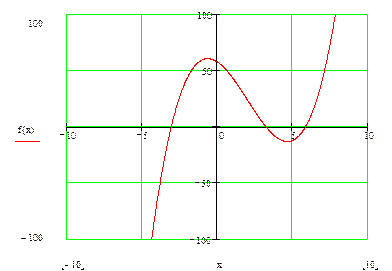
2.2 Метод хорд.
Сразу необходимо заметить, что существуют два случая (варианта) при решении методом хорд.
Случай первый. Первая и вторая производные функции имеют одинаковые знаки, т.е. ![]() .
.
В этом случае итерационный процесс осуществляем по формуле
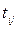
Случай второй. Первая и вторая производные функции имеют разные знаки, т.е. ![]() .
.
В этом случае итерационный процесс осуществляем по формуле
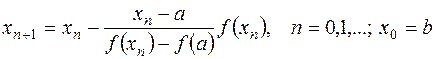
Для оценки точности приближение можно воспользоваться формулой
![]() ,
,
где ![]() при
при ![]() ,
, ![]() – точное значение корня.
– точное значение корня.
Итак решим наше уравнение ![]() методом хорд с точностью
методом хорд с точностью ![]() .
.
2.2.1 Интервал ![]() .
.
![]()
![]()
![]()
![]()
![]()
Так как первая и вторые производные в точке, от которой мы начинаем работать имеют различные знаки, то работаем по второму варианту.
Результаты вычисления приведены в таблице.
|
|
|
|
|
|
| -4,0000000 |
-3,0000000 |
-66,0000000 |
4,0000000 |
0,0740741 |
| -4,0000000 |
-3,1142857 |
-66,0000000 |
-2,3688397 |
0,0438674 |
| -4,0000000 |
-3,0440850 |
-66,0000000 |
1,5901736 |
0,0294477 |
| -4,0000000 |
-3,0901012 |
-66,0000000 |
-0,9879693 |
0,0182957 |
| -4,0000000 |
-3,0610770 |
-66,0000000 |
0,6456578 |
0,0119566 |
| -4,0000000 |
-3,0798611 |
-66,0000000 |
-0,4086778 |
0,0075681 |
| -4,0000000 |
-3,0678974 |
-66,0000000 |
0,2640772 |
0,0048903 |
| -4,0000000 |
-3,0755972 |
-66,0000000 |
-0,1684077 |
0,0031187 |
| -4,0000000 |
-3,0706743 |
-66,0000000 |
0,1083107 |
0,0020058 |
| -4,0000000 |
-3,0738353 |
-66,0000000 |
-0,0692833 |
0,0012830 |
| -4,0000000 |
-3,0718112 |
-66,0000000 |
0,0444729 |
0,0008236 |
| -4,0000000 |
-3,0731096 |
-66,0000000 |
-0,0284836 |
0,0005275 |
| -4,0000000 |
-3,0722776 |
-66,0000000 |
0,0182690 |
0,0003383 |
| -4,0000000 |
-3,0728111 |
-66,0000000 |
-0,0117068 |
0,0002168 |
| -4,0000000 |
-3,0724692 |
-66,0000000 |
0,0075061 |
0,0001390 |
| -4,0000000 |
-3,0726884 |
-66,0000000 |
-0,0048109 |
0,0000891 |
| -4,0000000 |
-3,0725479 |
-66,0000000 |
0,0030843 |
0,0000571 |
| -4,0000000 |
-3,0726380 |
-66,0000000 |
-0,0019770 |
0,0000366 |
![]()
2.2.2 Интервал ![]() .
.
![]()
![]()
![]()
![]()
![]()
Так как первая и вторые производные в точке, от которой мы начинаем работать имеют различные знаки, то работаем по второму варианту.
Результаты вычисления приведены в таблице.
|
|
|
|
|
|
| 3,0000000 |
4,0000000 |
4,0000000 |
-10,0000000 |
-0,2222222 |
| 3,0000000 |
3,2857143 |
4,0000000 |
-0,8746356 |
-0,0485909 |
| 3,0000000 |
3,2344498 |
4,0000000 |
-0,0423087 |
-0,0023505 |
| 3,0000000 |
3,2319959 |
4,0000000 |
-0,0019734 |
-0,0001096 |
| 3,0000000 |
3,2318815 |
4,0000000 |
-0,0000919 |
-0,0000051 |
![]()
2.2.3 Интервал ![]() .
.
![]()
![]()
![]()
![]()
![]()
Так как первая и вторые производные в точке, от которой мы начинаем работать имеют одинаковые знаки, то работаем по первому варианту.
Результаты вычисления приведены в таблице.
|
|
|
|
|
|
| 5,0000000 |
6,0000000 |
-12,0000000 |
4,0000000 |
0,6666667 |
| 5,7500000 |
6,0000000 |
-2,0156250 |
4,0000000 |
0,3359375 |
| 5,8337662 |
6,0000000 |
-0,1613014 |
4,0000000 |
0,0268836 |
| 5,8402098 |
6,0000000 |
-0,0120198 |
4,0000000 |
0,0020033 |
| 5,8406885 |
6,0000000 |
-0,0008909 |
4,0000000 |
0,0001485 |
| 5,8407240 |
6,0000000 |
-0,0000660 |
4,0000000 |
0,0000110 |
![]()
Итак, корнями уравнения ![]() будут
будут ![]() ,
, ![]() ,
, ![]() .
.
2.3 Метод касательных (метод Ньютона).
В век повальной компьютеризации не есть хорошо считать при помощи логарифмической линейки. Поэтому, разработаем алгоритм и прикладную программу для решения кубических уравнений методом Ньютона.
Ниже приведена блок-схема алгоритма и листинг программы, реализующей данный алгоритм на языке С++. Также привожу текст, которая выдает данная программа при решении исходного уравнения.
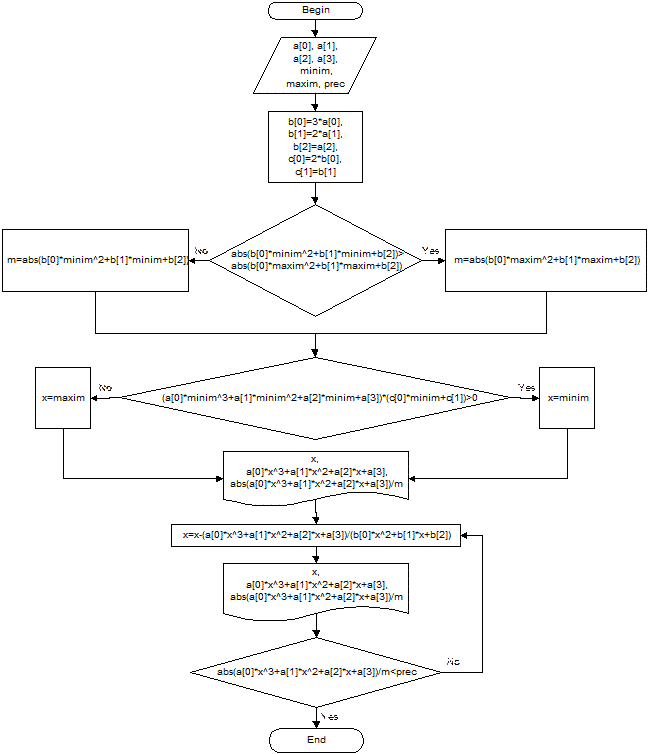
//метод Ньютона длЯ решениЯ кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
c[2]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
double Calc_Second(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).nn";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решениЯ."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"nНижнЯЯ граница должна быть меньше верхней и не может быть ей равна."<<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
c[0]=b[0]*2;
c[1]=b[1];
cout<<"nnn"
<<"Исходное уравнение имеет вид : nn"
<<a[0]<<"x^3+("<<a[1]<<")x^2+("<<a[2]<<")x+("<<a[3]<<")=0nn"
<<"ПерваЯ производнаЯ имеет вид : nn"
<<"f'(x)="<<b[0]<<"x^2+("<<b[1]<<")x+("<<b[2]<<")nn"
<<"ВтораЯ производнаЯ имеет вид : nn"
<<"f''(x)="<<c[0]<<"x+("<<c[1]<<")nn";
}
void Calculation()
{
double x=0, m=0;
cout<<"-------------------------------------------------"<<endl
<<"| Xn | f(Xn) | |f(Xn)|/m |"<<endl
<<"-------------------------------------------------"<<endl;
if (abs(Calc_Fun(minim))*abs(Calc_Second(minim))>0) x=minim;
else x=maxim;
if (Calc_First(minim)>Calc_First(maxim)) m=abs(Calc_First(maxim));
else m=abs(Calc_First(minim));
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<(fabs(Calc_Fun(x))/m);
cout<<"|n";
while((fabs(Calc_Fun(x))/m)>prec)
{
x=(x-(Calc_Fun(x)/Calc_First(x)));
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<fabs(Calc_Fun(x))/m;
cout<<"|n";
}
cout<<"-------------------------------------------------";
}
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
double Calc_Second(double x)
{
return (c[0]*x+c[1]);
}
![]()
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| -4| -66| 1.222222222|
| -3.24137931| -9.922506048| 0.183750112|
| -3.079817529| -0.40621762| 0.007522548518|
| -3.07261683|-0.000789793230|1.462580056e-05|
-------------------------------------------------
![]()
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 3| 4| 0.4444444444|
| 3.222222222| 0.159122085| 0.01768023167|
| 3.231855174| 0.000341137633|3.790418145e-05|
-------------------------------------------------
![]()
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 6| 4| 0.6666666667|
| 5.851851852| 0.2601229487| 0.04335382479|
| 5.840787634| 0.001413241032| 0.000235540172|
| 5.840726862|4.255405933e-08|7.092343222e-09|
-------------------------------------------------
2.4 Метод итераций. Как и для предыдущего метода, привожу блок-схему алгоритма решения и листинг программы, реализующей этот алгоритм на языке программирования С++.
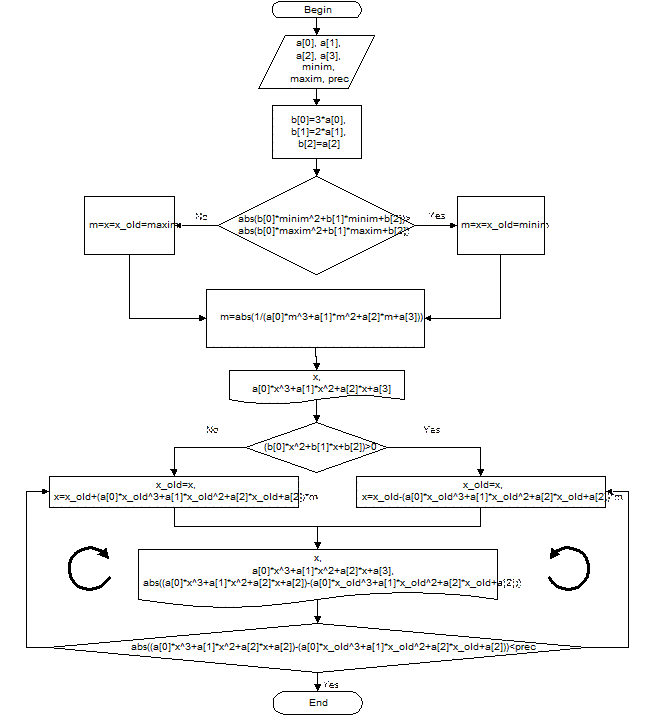
//метод итераций длЯ решениЯ кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа длЯ решениЯ кубических уравнений методом итераций.nn";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решениЯ."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"nНижнЯЯ граница должна быть меньше верхней и не может быть ей
равна." <<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
}
void Calculation()
{
double x=0, x_old=0, m=0;
cout<<"-------------------------------------------------"<<endl
<<"| Xn | f(Xn) | X(n+1)-Xn |"<<endl
<<"-------------------------------------------------"<<endl;
if(fabs(Calc_First(minim))>fabs(Calc_First(maxim))) m=x=x_old=minim;
else m=x=x_old=maxim;
m=fabs(1/Calc_First(m));
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"| |n";
if(Calc_First(x)>0)
{
do
{
x_old=x;
x=x_old-m*Calc_Fun(x_old);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<fabs( Calc_Fun(x) - Calc_Fun(x_old) );
cout<<"|n";
}
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
else
{
do
{
x_old=x;
x=x_old+m*Calc_Fun(x_old);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<fabs( Calc_Fun(x) - Calc_Fun(x_old) );
cout<<"|n";
}
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
cout<<"-------------------------------------------------";
}
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
![]()
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| -4| -66| |
| -3.24137931| -9.922506048| 56.07749395|
| -3.127327517| -3.12093462| 6.801571427|
| -3.091454705| -1.064778438| 2.056156183|
| -3.079215872| -0.372281515| 0.6924969227|
| -3.074936774| -0.131239433| 0.241042082|
| -3.073428275| -0.04639844126| 0.08484099175|
| -3.07289496| -0.01642029825| 0.02997814301|
| -3.072706221|-0.005813178631| 0.01060711962|
| -3.072639403|-0.002058264249| 0.003754914382|
| -3.072615744|-0.000728799396| 0.001329464852|
| -3.072607367|-0.000258060628|0.0004707387678|
| -3.072604401|-9.137721784e-0|0.0001666834108|
| -3.072603351|-3.235601088e-0|5.902120696e-05|
| -3.072602979|-1.145703711e-0|2.089897377e-05|
-------------------------------------------------
![]() Программа длЯ решениЯ кубических уравнений методом итераций.
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 3| 4| |
| 3.222222222| 0.159122085| 3.840877915|
| 3.231062338| 0.01338370012| 0.1457383849|
| 3.231805877| 0.001151957391| 0.01223174272|
| 3.231869875|9.934183961e-05| 0.001052615552|
| 3.231875394|8.568402322e-06|9.077343728e-05|
| 3.23187587|7.390497921e-07| 7.82935253e-06|
-------------------------------------------------
![]()
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 6| 4| |
| 5.851851852| 0.2601229487| 3.739877051|
| 5.842217669| 0.0346921878| 0.2254307609|
| 5.840932773| 0.004788677115| 0.02990351069|
| 5.840755414|0.0006639855431| 0.004124691572|
| 5.840730822|9.212373716e-05|0.0005718618059|
| 5.84072741|1.278267885e-05|7.934105832e-05|
| 5.840726937|1.773688694e-06|1.100899016e-05|
-------------------------------------------------
![]()
Решив уравнение ![]() , получили корень
, получили корень ![]()
| Метод |
Корень № 1 |
Корень № 2 |
Корень № 3 |
| Хорд |
-3,072638 |
3,231881 |
5,840724 |
| Касательных (Ньютона) |
-3,072616 |
3,231855 |
5,840726 |
| Итераций |
-3,072602 |
3,231875 |
5,840726 |
Для дальнейших расчетов будем использовать среднее арифметическое значение полученных корней.
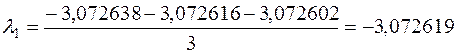
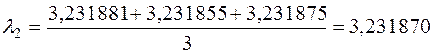
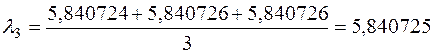
3. Используя полученные значения, определим собственные значения исходной матрицы.
Собственные вектора матрицы А=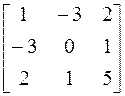 определим по формуле
определим по формуле
![]()
Для нашей матрицы, данная формула примет следующий вид
![]()
Коэффициенты ![]() определяются по схеме Горнера:
определяются по схеме Горнера:
![]()
Для ![]() имеем:
имеем:
![]()
![]()
![]()
Для ![]() имеем:
имеем:
![]()
![]()
![]()
Для ![]() имеем:
имеем:
![]()
![]()
![]()
Далее можем найти собственные векторы:
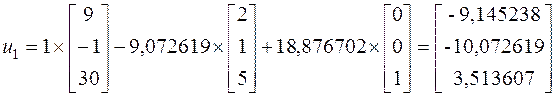
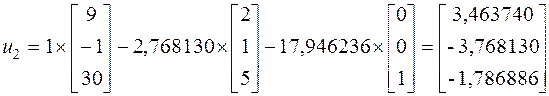
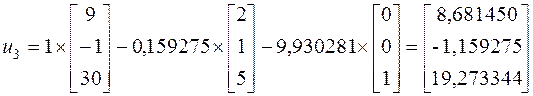
4. Для контроля полученных значений, развернем исходную матрицу А=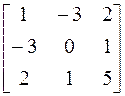 , и определим ее собственные векторы методом непосредственного развертывания.
, и определим ее собственные векторы методом непосредственного развертывания.
Характеристический многочлен для данной матрицы имеет вид:
![]() .
.
Находим ![]() .
.
Число диагональных миноров второго порядка у матрицы второго порядка 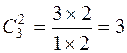 .
.
Выписываем эти миноры и складываем их:
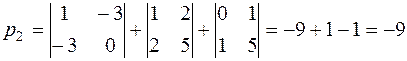 .
.
И, в заключение, находим
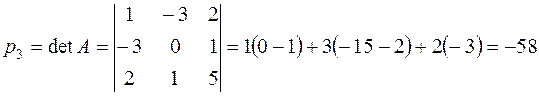
Таким образом, характеристическое уравнение имеет вид
![]()
Данное уравнение идентично уравнению, полученному при помощи метода Крылова. Нет смысла заново его решать. Воспользуемся уже вычисленными корнями (их средним значением).
Определим собственный вектор ![]() , соответствующий
, соответствующий ![]() .
.
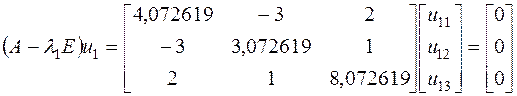 , или
, или
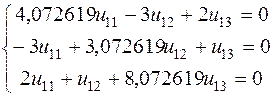
Из третьего уравнения системы выведем ![]() и подставим его в первое уравнение системы
и подставим его в первое уравнение системы
![]()
![]()
Примем ![]() , тогда
, тогда ![]() и
и ![]() .
.
Итак, искомый вектор матрицы ![]() , найденный с точностью до постоянного множителя
, найденный с точностью до постоянного множителя ![]() , для собственного значения матрицы
, для собственного значения матрицы ![]() будет:
будет:
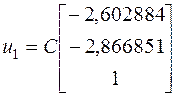
При помощи метода Крылова, мы получили точное значение собственного вектора 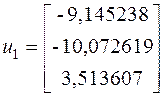 .
.
Мы можем проверить наши вычисления, взяв ![]() :
:
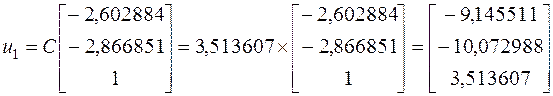
Как видно, мы получил идентичный, до третьего знака, результат.
Определим собственный вектор ![]() , соответствующий
, соответствующий ![]() .
.
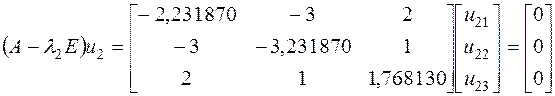 , или
, или
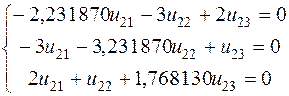
Из третьего уравнения системы выведем ![]() и подставим его в первое уравнение системы
и подставим его в первое уравнение системы
![]()
![]()
Примем ![]() , тогда
, тогда ![]() и
и ![]() .
.
Итак, искомый вектор матрицы ![]() , найденный с точностью до постоянного множителя
, найденный с точностью до постоянного множителя ![]() , для собственного значения матрицы
, для собственного значения матрицы ![]() будет:
будет:
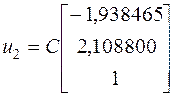
При помощи метода Крылова, мы получили точное значение собственного вектора 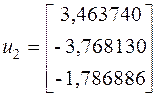 .
.
Мы можем проверить наши вычисления, взяв ![]() :
:
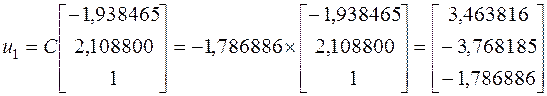
Как видно, мы получил идентичный, до третьего знака, результат.
Определим собственный вектор ![]() , соответствующий
, соответствующий ![]() .
.
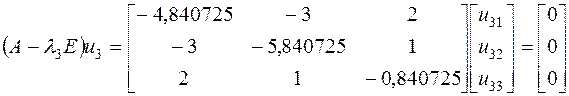 , или
, или
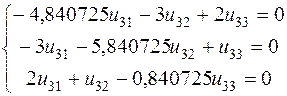
Из третьего уравнения системы выведем ![]() и подставим его в первое уравнение системы
и подставим его в первое уравнение системы
![]()
![]()
Примем ![]() , тогда
, тогда ![]() и
и ![]() .
.
Итак, искомый вектор матрицы ![]() , найденный с точностью до постоянного множителя
, найденный с точностью до постоянного множителя ![]() , для собственного значения матрицы
, для собственного значения матрицы ![]() будет:
будет:
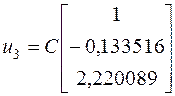
При помощи метода Крылова, мы получили точное значение собственного вектора 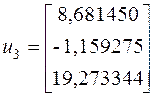 .
.
Мы можем проверить наши вычисления, взяв ![]() :
:
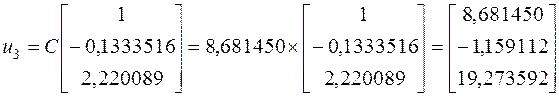
Как видно, мы получил идентичный, до третьего знака, результат.
Похожие работы
-
Системы линейных уравнений и неравенств
Основные понятия теории систем уравнений. Метод Гаусса — метод последовательного исключения переменных. Формулы Крамера. Решение систем линейных уравнений методом обратной матрицы. Теорема Кронекер–Капелли. Совместность систем однородных уравнений.
-
Эффективный алгоритм обращения матрицы Вандермонда
Разработан алгоритм, сочетающий точность и быстродействие, что позволяет рекомендовать его для практического использования.
-
Математика матрица
Матрицы Матрица - прямоугольная (в частном случае квадратная) таблица с числами. Матрица m × n - это таблица из m строк и n столбцов. Если m = n, матрицу называют квадратной матрицей порядка n.
-
Определитель матрицы 2
Оглавление Задача 2 3 Задача 3 5 Задача 4 7 Задача 1 Вычислить определитель 4-го порядка. Решение: Определитель 4-го порядка находится по формуле: aij – элемент матрицы;
-
Определители
Муниципальное образовательное учреждение – гимназия № 47 Реферат по математике ученицы 8 г класса Годуновой Екатерины г.Екатеринбург, 2000г. Введение
-
Матрицы
Общие определения, связанные с понятием матрицы. Действия над матрицами. Определители 2-го и 3-го порядков, порядка n, порядок их вычисления и характерные свойства. Обратные матрицы и их ранг. Понятие и этапы элементарного преобразования матрицы.
-
Решение матриц
Правила произведения матрицы и вектора, нахождения обратной матрицы и ее определителя. Элементарные преобразования матрицы: умножение на число, прибавление, перестановка и удаление строк, транспонирование. Решение системы уравнений методом Гаусса.
-
Алгебра матриц. Системы линейных уравнений
Выполнение действий над матрицами. Определение обратной матрицы. Решение матричных уравнений и системы уравнений матричным способом, используя алгебраические дополнения. Исследование и решение системы линейных уравнений методом Крамера и Гаусса.
-
Вычисление характеристических многочленов собственных значений и собственных векторов
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ СУМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ИНФОРМАТИКИ Курсовая работа по дисциплине «Численные методы»
-
Системы линейных уравнений
Критерий совместности. Метод Гаусса. Формулы Крамера. Матричный метод.