Referat.me
/ / по Алгебре и геометрие

Название: по Алгебре и геометрие

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 88.8 Kb

Скачать файл: referat.me-216364.docx

Краткое описание работы: Федеральное агентство связи Сибирский Государственный Университет Телекоммуникаций и Информатики Межрегиональный центр переподготовки специалистов

по Алгебре и геометрие

Федеральное агентство связи

Сибирский Государственный Университет Телекоммуникаций и Информатики

Межрегиональный центр переподготовки специалистов

Контрольная работа

По дисциплине: Алгебра и геометрия

Выполнил : Шевыряев А.Н.

Группа : СДТ-03

Вариант:6

Проверил : ___________________

Новосибирск, 2010 г

Задача 1. Дана система трех линейных уравнений. Найти решение ее двумя способами: методом Крамера и методом Гаусса.

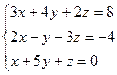
a) Решение системы методом Крамера.

Формулы Крамера:

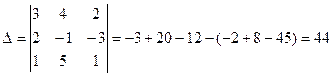
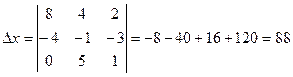
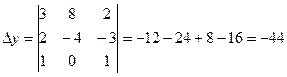
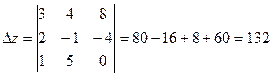
Найдем значения неизвестных:

Выполним проверку:

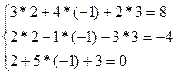
b) Решение системы методом Гаусса.

Составим расширенную матрицу системы:

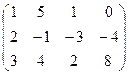
Выполним преобразования:

1) умножим первую строку на (-2) и сложим со 2-й строкой матрицы;

2) умножим первую строку на (-3) и сложим с 3-й строкой матрицы;

3) умножим 2-ю строку на (-1) и сложим с 3-й строкой матрицы.

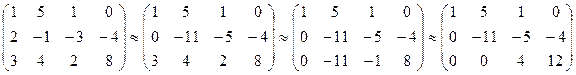
В результате получили матрицу системы треугольного вида.

Запишем итоговую систему:

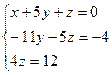
Найдем значения неизвестных:

Задача 2. Даны координаты вершин пирамиды . Найти:

1) длину ребра ;

2) угол между ребрами и ;

3) площадь грани ;

4) уравнение плоскости .

5) объём пирамиды .

Решение.

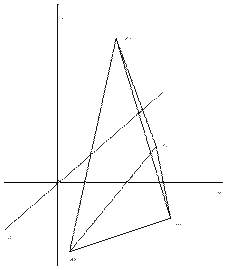
Рисунок 1.

1) Длина ребра равна расстоянию между точками и или модулю вектора . Расстояние между точками и вычисляется по формуле . Подставляя в эту формулу исходные данные, получим

2) Угол между ребрами будем искать, используя формулы векторной алгебры:

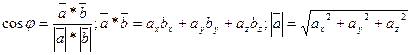
В нашем случае:

Чтобы найти координаты вектора, из координат конца вектора следует вычесть координаты начала вектора. Таким образом,

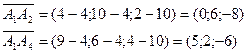
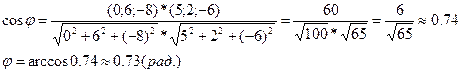
3) Площадь грани можно найти, используя свойства скалярного произведения: площадь параллелограмма, построенного на векторах и численно равна модулю их векторного произведения. В нашем случае

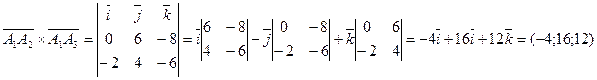
4) Уравнение плоскости будем искать как уравнение плоскости, проходящей через три данные точки :

;

;

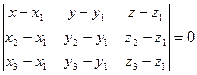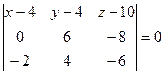Полученное уравнение является уравнением плоскости .

5) Объем пирамиды найдем, используя свойство смешанного произведения трех векторов – модуль смешанного произведения численно равен объему параллелепипеда, построенного на этих векторах. Соответственно

Найдем смешанное произведение векторов :

Похожие работы