Название: Основная теорема алгебры

Вид работы: реферат

Рубрика: Математика

Размер файла: 66.68 Kb

Скачать файл: referat.me-217380.docx

Краткое описание работы: Доказательство основной теоремы алгебры.

Основная теорема алгебры

Всякий многочлен с любыми комплексными коэффициентами , степень которого не меньше единицы имеет хотя бы один корень, в общем случае комплексный.

План доказательства .

Лемма №1 . Многочлен f(x) является непрерывной функцией комплексного переменного x .

Лемма №2 . Если данн многочлен n -ой степени, n>0,

f(x)=a₀ xⁿ +a₁ x^n-1 +…+a_n

с произвольными комплексными коэффициентами и если k - любое положительное действительное число, то для достаточно больших по модулю значений

|a_n xⁿ |>k|ax^n-1 +a_n x^n-2 +….+a₀ |

Лемма №3 .

Лемма №4 .(Лемма Даламбера).

Лемма №5.

Если действительная функция комплексного переменного f(x) непрерывна в замкнутом круге Е, то она ограничена.

Лемма №6.

Действительная функция комплексного переменного f(x) непрерывная в замкнутом круге Е достигает своего минимума и максимума.

Доказательство основной теоремы .

Лемма №1.

Надо доказать, что |f(x₀ +x)-f(x₀ ) |<e .

Докажем Лемму №1 сначала для многочлена без свободного члена и при x₀ =0

Если A=max(|a₀ |,|a₁ |,…,|a _n-1 |) и (1)

то |f(x)|=|a₀ xⁿ +…+a_n-1 x|

,
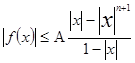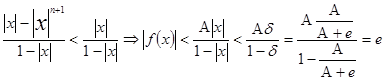т.к |x |<б , и из (1) б <1, то

т.к. a₀ =0 то f(0)=0

Что и требовалось доказать.

Теперь докажем непрерывность любого многочлена.

f(x₀ +x)=a₀ (x₀ +x)ⁿ +…+a_n

pаскрывая все скобки по формуле бинома и собирая вместе члены с

одинаковыми степенями x получим

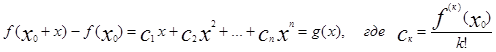
Многочлен g(x)-это многочлен от x при x₀ =0 и а₀ =0 |f(x₀ +x)-f(x)|=|g(x)|<e

Лемма доказана.

Лемма №2

Если дан многочлен n -ой степени, n>0,

f(x)=a₀ xⁿ +a₁ x^n-1 +…+a_n

с произвольными комплексными коэффициентами и если k - любое положительное действительное число, то для достаточно больших по модулю значений x верно неравенство:

|a₀ xⁿ |>k|a₁ x^n-1 +a₂ x^n-2 +….+a_n | (2)

Доказательсво.

Пусть А=max(), тогда

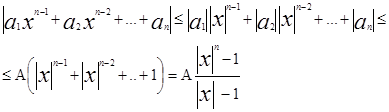
пологая |x| >1, получим

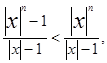
откуда

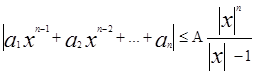
следовательно неравенство (2) будет выполняться если |x|>1 и

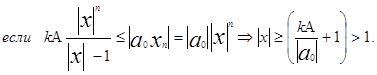
Лемма №2 доказана.

Лемма №3 .

Доказательство.

(3)

применим лемму 2: при k=2 существует такое N₁ , что при |x|> N₁

|a₀ xⁿ |>2|a₁ x^n-1 +a₂ x^n-2 +….+a_n |

откуда

|a₁ x^n-1 +a₂ x^n-2 +….+a_n |<|a₀ xⁿ |/2

тогда из (3)

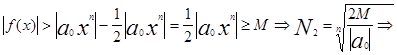
при |x|>N=max(N₁ ,N₂ ) |f(x)|>M что и тебовалось доказать.

Лемма №3(Лемма Даламбера).

Если при x=x₀ многочлен f(x) степени n ,не обращаеться в нуль, то существует такое приращение h, в общем случае комплексное, что

|f(x₀ +h)|<|f(x)|

Доказательство.

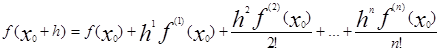
По условию f(x₀ ) не равно нулю, случайно может быть так, что x₀ является корнем f’(x),..,f^(k-1) (x). Пусть k-я производная будет первой, не имеющей x₀ своим корнем. Такое k существует т.к.

f⁽ⁿ⁾ ( x₀ )=n!a₀

Таким образом

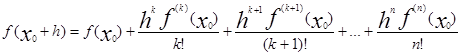Т.к f(x₀ ) не равно нулю то поделим обе части уравнения на f(x₀ )

и обозначим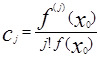

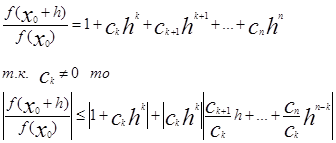
Теперь будем выбирать h. Причем будем отдельно выбирать его модуль и его аргумент.

По лемме№1: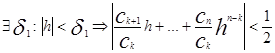

С другой стороны при

(4)

Пусть |h|<min(б₁ , б₂ ), тогда

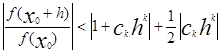
Теперь выберем аргумент h так, чтобы c_k h^k было действительным отрицательным числом.

При таком выборе c_k h^k =-| c_k h^k | следовательно учитывая (4) получим

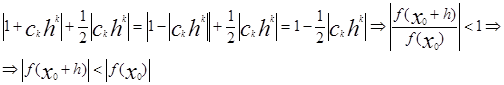
Что доказывает лемму Даламбера.

Лемма №5.

Если действительная функция комплексного переменного f(x) непрерывна в замкнутом круге Е, то она ограничена.

Доказательство.

Предположим, что это не верно тогда

получена бесконечная ограниченная последовательность x_n ,

из нее можно выбрать сходящуюся подпоследовательность , пусть ее предел равенx₀ . Так как круг Е замкнут, то x₀ пренадлежит Е. Тогда так как f(x) непрерывна

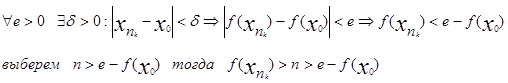
получено противоречие, следовательно неверно, предположение о неограничености f(x) .

Лемма №6.

Действительная функция комплексного переменногоf(x) непрерывная в замкнутом круге Е достигает своего минимума и

максимума.

Доказательство.

Докажем это утверждение для максимума.

Так как f(x) непрерывна в Е, то она ограничена и следовательно существует M =sup{ f(x)} . Рассмотрим функцию .

Если f(x) не достигает своего максимума, то M> f(x) следовательно M- f(x)>0 , следовательно g(x) непрерывна в Е.

Полученое противоречит тому, что M =sup{ f(x)} . Следовательно функция достигает свего максимума. Аналогично доказывается достижение минимума.

Доказательство основной теоремы.

Пусть дан многочлен f(x), очевидно что если a_n -свободный член, то f(0)= a_n . Теперь применим лемму№3: возьмем М=|f(0)| =|a_n | тогда существует такое N, что при |x|>N |f(x)|>M. Теперь возьмем круг Е ограниченный окружностью с центром в нуле и радиусом N, включая границы круга. Так как (по лемме №1) многочлен f(x)-непрерывен, то и |f(x)|-непрерывен внутри замкнутого круга Е, следовательно(по лемме №6), существует такая точка x₀ , что для всех x из E выполняется неравенство |f(x)|>=|f(x₀ )|. x₀ является точкой минимума для |f(x)| внутри E. Т.к для любого x:|x|>N |f(x)|>M>|f(0)|>|f(x₀ )| точка x₀ является точкой минимуа |f(x)| на всей комплексной плоскости.

|f(x₀ )|=0 т.к по лемме Даламбера если |f(x₀ )|¹0 то x₀ не точка минимума для |f(x)|Þ x₀ -корень многочлена f(x).

Теорема доказана.