Название: Математика

Вид работы: контрольная работа

Размер файла: 135.44 Kb

Скачать файл: referat.me-215679.docx

Краткое описание работы: Математика и информатика. Решение системы линейных алгебраических уравнений методом Крамера. Работа в текстовом редакторе MS WORD. Рисование с помощью графического редактора. Определение вероятности. Построение графика функции с помощью MS Excel.

Математика

Вариант 1

Задача 1.

Решить систему линейных алгебраических уравнений методом Крамера.

x + 2y – z = 2

2x – 3y + 2z = 2

3x + y + z = 8

1 2 -1

Δ = 2 -3 2 = - 3 – 2 + 12 – 9 – 2 – 4 = - 8

3 1 1

2 2 -1

Δ_х = 2 -3 2 = - 6 – 2 + 32 – 24 – 4 – 4 = - 8

8 1 1

1 2 -1

Δ_y = 2 2 2 = 2 – 16 + 12 + 6 – 16 – 4 = -16

3 81

1 2 2

Δ_z = 2 -3 2 = - 24 + 4 + 12 + 18 – 2 – 32 = -24

3 1 8

Х = Δ_х Δ = -8-8 = 1

Y = Δ_y Δ = -16-8 = 2

Z = Δ_z Δ = -24-8 = 3

Задача 2.

К 100 гр. 20%-го раствора соли добавили 300 гр. 10%-го раствора соли. Определить концентрацию полученного раствора.

I	II	I + II
m	100	300	400
%	20%	10%	X%

0.2 * 100 + 0.1 * 300 = (x100) * 400

20 + 30 = 4x

50 = 4x

x = 12.5%

Задача 3.

Дано множество А и множество В. Найти A∩B, AUB, AB.

A = {x│12 < x < 16 }

B = {x│10 < x < 14 }

1) A∩B = {x│10 < x < 14 }

2) AUB = {x│12 < x < 16 }

3) AB = {x│10 < x < 14 }

Задача 4

Сколькими способами 8 телевизоров разных фирм можно расположить на витрине магазина?

Р8 = 8! = 1*2*3*4*5*6*7*8 = 40320

Ответ: Р = 40320 способов

Задача 5

Среди 15 лотерейных билетов 3 выигрышных. Определить вероятность того, что из 7 удачно взятых лотерейных билетов хотя бы 1 будет выигрышный.

всего 15: 3 выигрышных, 12 невыигрышных; берем 7

В = 1 выигрышный, 6 невыигрышных

С = 2 выигрышных, 5 невыигрышных

Е = 3 выигрышных, 4 невыигрышных

А = В + С + Е

Р(А) = Р(В) + Р(С) + Р(Е)

С¹3 * С²12 22 198

Р(В) = ------------- = ------ = --------

С7 15 715 6435

С²3 * С¹12 12 36

Р(С) = ------------ = ------- = --------

С7 15 2145 6435

С³3 1

Р(Е) = ------- = --------

С7 15 6435

198 36 1 235 47

Р(А) = -------- + -------- + -------- = -------- = ------- ≈ 0,04

6435 6435 6435 6435 1287

Ответ: Р(А) ≈ 0,04

Задача 6

Оформить работу в текстовом редакторе MSWORD, шрифт – TimesNewRoman. Интервал полуторный. Поля: левое – 2,0; правое – 1,5; верхнее – 1,5; нижнее – 1,5. Ключевые фразы и слова выделить полужирным курсивом.

Задача 7.

Нарисовать картинку, используя любой графический редактор.

Задача 8.

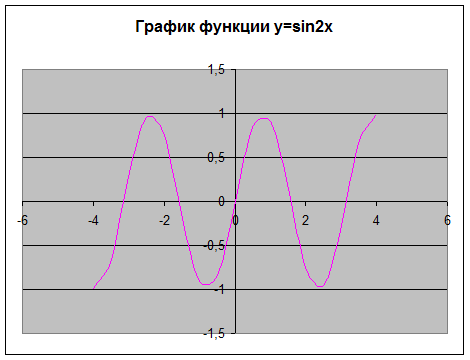
С помощью MSExcel на промежутке [-4;4] с шагом 0,5 построить график функции y=sin2x.

X	Y
-4	-0,98936
-3,5	-0,65699
-3	0,279415
-2,5	0,958924
-2	0,756802
-1,5	-0,14112
-1	-0,9093
-0,5	-0,84147
0	0
0,5	0,841471
1	0,909297
1,5	0,14112
2	-0,7568
2,5	-0,95892
3	-0,27942
3,5	0,656987
4	0,989358

Задача 9.

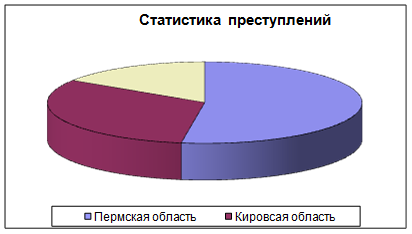
По данным статистики численность населения в Пермской области 3121500 человек, в Кировской – 1603800 человек, в Коми-Пермяцком АО 650000 человек. В 1999 в Пермской области зарегистрировано 98731 преступление, в Кировской – 30745, в КПАО – 6228 преступлений. Для характеристики уровня преступности используется число преступлений на 100000 населения (коэффициент преступности). В какой области этот показатель выше. Построить сравнительную диаграмму.

Пермская область	Кировсая область	Коми-Пермяцкий АО
Пермская область	Кировсая область	Коми-Пермяцкий АО	численность населения	3121500	1603800	650000
количество преступлений	98731	30745	6228
коэф-т преступности	3162,93	1917,01	958,15

Математика

Похожие работы